[AlgorithmStaff] Bresenham快速直线算法

操作系统:Windows8.1

显卡:Nivida GTX965M

开发工具：Unity2017.3 | NativeC

---

最近在学习 Unity tilemap Brush 自定义笔刷功能时候，看到其直线笔刷 LineBrush 是采用 Bresenham 算法实现，故借此机会在这里记录下学习过程，并在最后给出完整实现。

Introduction

---

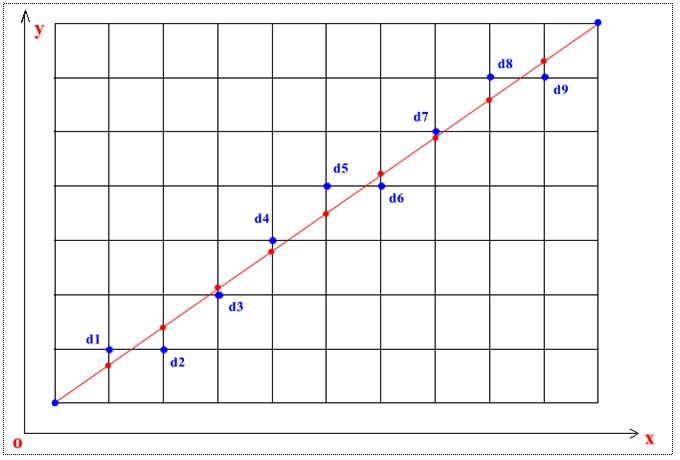
Bresenham 是光栅化的直线算法，或者说是通过像素来模拟直线。比如下图所示像素点来模拟红色的直线。

给定两个起点 P1(x1, y1) | P2(x2, y2)，如何绘制两点之间的连线呢。这里假设斜率约束在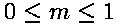，那么算法的过程如下：

1. 绘制起点 (x1, y1) 。
2. 绘制下一个点， X坐标加1，判断是否到终点，如果是则算法完成。否则找下一个点，由上图可知将要绘制的点不是右邻点，要么就是右上邻接点。
3. 绘制点。
4. 跳回第二步骤。
5. 结束。

算法具体过程就是在每次绘制点的时候选取与直线的交点y坐标的差最小的那个点，如下图所示：

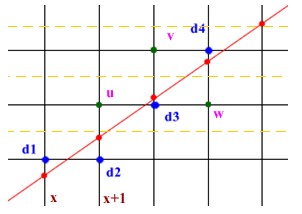
那么问题聚焦在如何找最近的点，逻辑上每次 x 都递增 ，y 则增加 或不增加。具体上图，假设已经绘制到了 d1 点，那么接下来 x 加 1，但是选择 d2 还是 u 点呢，直观上可以知道 d2 与目标直线和 x + 1 直线的交点比较近，即纵坐标之差小。换句话说 (x + 1, y + 1) 点纵坐标差大于 0.5。 所以选择 d2 ，其他点也按照该规则执行。

The Basic Bresenham

---

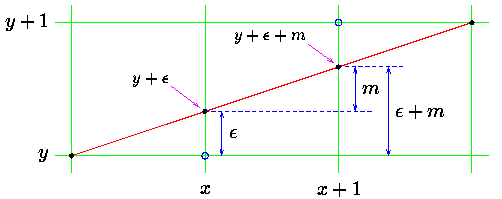
假设以 (x, y) 为绘制起点，一般情况下的直观想法是先求 m = dy /dx（ y 的增量），然后逐步递增 x, 设新的点为 x1 = x + j ，则 y1 = round(y + j * m) 。可以看到，这个过程涉及大量的浮点运算，效率上是比较低的（特别是在嵌入式应用中，DSP可以一周期内完成2次乘法，一次浮点却要上百个周期）。

下面我们来看一下 Bresenham 算法，如图1, (x, y +ε) 的下一个点为 (x, y + ε + m)， 这里 ε 为累加误差。可以看出，当 ε+m < 0.5 时，绘制 (x + 1, y) 点，否则绘制 (x + 1, y + 1) 点。每次绘制后， ε 将更新为新值：

ε = ε + m ，如果 (ε + m) <０.５ (或表示为 2 * (ε + m) < 1 )

ε = ε + m – 1，其他情况

将上述公式都乘以 dx ，并将 ε * dx 用新符号 ξ 表示，可得

ξ = ξ + dy，如果 2 * (ξ + dy) < dx

ξ = ξ + dy – dx，其他情况

可以看到，此时运算已经全变为整数了。以下为算法的伪代码：

ξ ← 0，y ← y1

For x ← x1 to x2 do

　　Plot Point at (x, y)

　　If (2(ξ + dy) < dx)

　　　　ξ ←ξ + dy

　　Else

　　　　y ← y + 1,ξ ←ξ + dy – dx

　　End If

End For

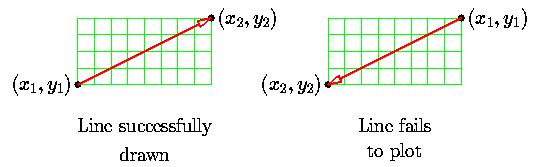
Handing multiple slopes

---

在实际应用中，我们会发现，当 dy > dx 或出现上图右侧情况时，便得不到想要的结果，这是由于我们只考虑 dx > dy， 且 (x, y) 的增量均为正的情况所致。经过分析，需要考虑 8 种不同的分区情况，如下图所示：

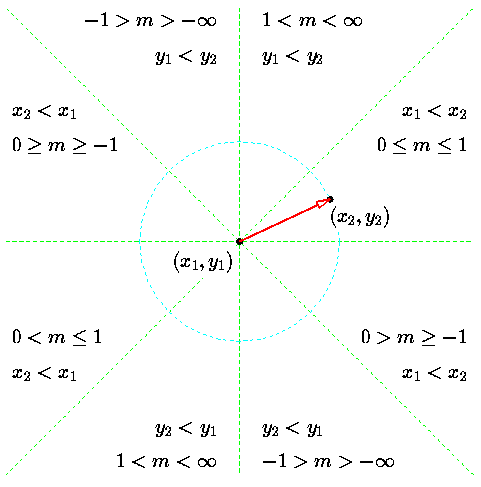
当然，如果直接在算法中对8种情况分别枚举， 那重复代码便会显得十分臃肿，因此在设计算法时必须充分考虑上述各种情况的共性。比如右侧 X 正负 45 度分区仅仅是互为 Y 轴镜像的关系，在具体实现的时候设定正确增量方向即可。

Implementation

---

下面给出基于C语言的实现：

void draw_line(int x1, int y1, int x2, int y2)
{
    int dx = x2 - x1;
    int dy = y2 - y1;
    int ux = ((dx > ) << ) - ;
    int uy = ((dy > ) << ) - ;
    int x = x1, y = y1, eps;

    eps = ; dx = abs(dx); dy = abs(dy);
    if (dx > dy)
    {
        for (x = x1; x != x2; x += ux)
        {
            printf("x = %d y = %d\n", x, y);
            eps += dy;
            if ((eps << ) >= dx)
            {
                y += uy; eps -= dx;
            }
        }
    }
    else
    {
        for (y = y1; y != y2; y += uy)
        {
            printf("x = %d y = %d\n", x, y);
            eps += dx;
            if ((eps << ) >= dy)
            {
                x += ux; eps -= dy;
            }
        }
    }
}

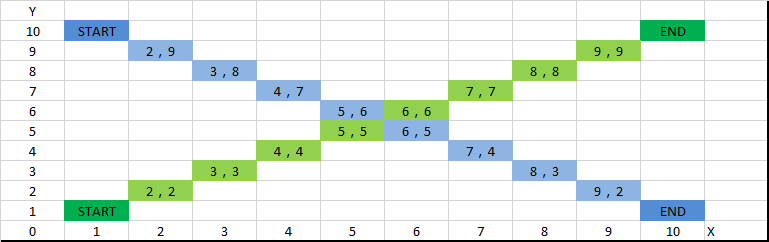
测试数据分别为绿色线段，起点 (1,1)  终点 (10,10)  和 蓝色线段，起点 (1, 10)  终点 (10,1) 。

测试数据分别为褐色线段，起点 (2,10)  终点 (4,1) 及起点 (6,9)  终点 (10,1) 。

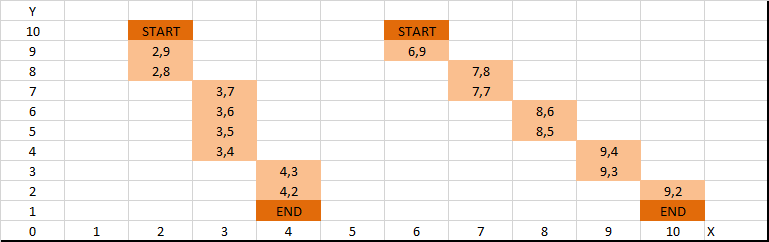
通过将程序运行的测试数据填充的表格后，可以很直观的看到两点之间线段的连接路径。

Based on Unity

---

Unity 官方的例子中已经给出了基于C#实现，代码如下：

// http://ericw.ca/notes/bresenhams-line-algorithm-in-csharp.html
        public static IEnumerable<Vector2Int> GetPointsOnLine(Vector2Int p1, Vector2Int p2)
        {
            int x0 = p1.x;
            int y0 = p1.y;
            int x1 = p2.x;
            int y1 = p2.y;

            bool steep = Math.Abs(y1 - y0) > Math.Abs(x1 - x0);
            if (steep)
            {
                int t;
                t = x0; // swap x0 and y0
                x0 = y0;
                y0 = t;
                t = x1; // swap x1 and y1
                x1 = y1;
                y1 = t;
            }
            if (x0 > x1)
            {
                int t;
                t = x0; // swap x0 and x1
                x0 = x1;
                x1 = t;
                t = y0; // swap y0 and y1
                y0 = y1;
                y1 = t;
            }
            int dx = x1 - x0;
            int dy = Math.Abs(y1 - y0);
            int error = dx / ;
            int ystep = (y0 < y1) ?  : -;
            int y = y0;
            for (int x = x0; x <= x1; x++)
            {
                yield return new Vector2Int((steep ? y : x), (steep ? x : y));
                error = error - dy;
                if (error < )
                {
                    y += ystep;
                    error += dx;
                }
            }
            yield break;
        }

最后将之前的两组数据带入Unity验证结果一致性：

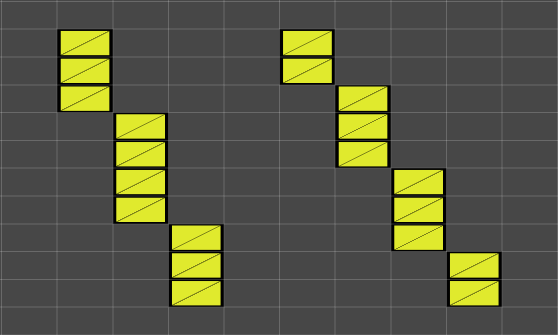
可以看到前文程序算法输出的数据结果与Unity采用的 C# 实现结果一致。

Summary

---

参考资料：

http://blog.csdn.net/jinbing_peng/article/details/44797993

https://www.cnblogs.com/gamesky/archive/2012/08/21/2648623.html

http://www.cnblogs.com/pheye/archive/2010/08/14/1799803.html