括号序列模型--序列dp--U86873 小Y的精灵国机房之旅

括号序列模型及解法

>Codeforces314E
◦给定一个长度为n的仅包含左右括号和问号的字符串，将问号变成左括号
或右括号使得该括号序列合法，求方案总数。
◦例如(())与()()都是合法的括号序列。
◦ n<=3000。

>Solution

◦括号序列问题，往往就是把左括号看成+1，右括号看成-1，我们只需要
保证任意一个前缀大于等于0，且总和为0，就代表是个合法括号序列了。
◦令dp[i][j]表示当前到第i个字符，现在的前缀和
◦那么分三种情况考虑。
◦若第i+1个字符是左括号，则能转移到dp[i+1][j+1]。
◦若第i+1个字符是右括号，则能转移到dp[i+1][j-1]。
◦若第i+1个字符是问号，则能转移到dp[i+1][j-1]与dp[i+1][j+1]。
◦最终dp[n][0]就是方案总数啦。
◦时间复杂度为O(n^2)。

U86873 小Y的精灵国机房之旅

题解

括号序列模型唉！

所以就可以套用上面的式子啦

把Y看做左括号，H看做右括号，C看做问号

准备AC

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
 
inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}
 
const int maxn=,mod=1e9+;
int n;
char a[maxn];
int f[][];
 
int main()
{
    n=read();
    scanf("%s",a+);
    f[][]=;
    for(int i=;i<=n;i++){
        if(a[i]=='Y'){
            f[i][]=;
            for(int j=;j<=i;j++){
                f[i][j]=f[i-][j-];
            }
        }
        if(a[i]=='H'){
            for(int j=;j<i;j++){
                f[i][j]=f[i-][j+];
            }
            f[i][i]=;
        }
        if(a[i]=='C'){
            for(int j=;j<i;j++){
                f[i][j]=(f[i-][j-]+f[i-][j+])%mod;
            }
            f[i][]=f[i-][];
            f[i][i]=f[i-][i-];
        }
    }
    printf("%d\n",f[n][]%mod);
    return ;
}

然后发现不对劲。。。。。

二维数组一定会炸。。。。

那就。。。循环队列！

我们发现每次到新的一个 i ，它只和 i-1 有关，所以 i-1 用过一次就可以销毁了，不然也是占空间

可以像这样&1来实现循环利用

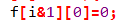
代码

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
 
inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}
 
const int maxn=,mod=1e9+;
int n;
char a[maxn];
int f[][maxn];
 
int main()
{
    n=read();
    scanf("%s",a+);
    memset(f,,sizeof(f));
    f[][]=;
    for(int i=;i<=n;i++){
        if(a[i]=='Y'){
            f[i&][]=;
            for(int j=;j<=i;j++){
                f[i&][j]=f[(i-)&][j-];
            }
        }
        if(a[i]=='H'){
            for(int j=;j<i;j++){
                f[i&][j]=f[(i-)&][j+];
            }
            f[i&][i]=;
        }
        if(a[i]=='C'){
            f[i&][]=f[(i-)&][];
            for(int j=;j<i;j++){
                f[i&][j]=(f[(i-)&][j-]+f[(i-)&][j+])%mod;
            }
            f[i&][i]=f[(i-)&][i-];
        }
    }
    printf("%d\n",f[n&][]%mod);
    return ;
}