论文翻译：LP-3DCNN: Unveiling Local Phase in 3D Convolutional Neural Networks

引言

传统的3D卷积神经网络（CNN）计算成本高，内存密集，容易过度拟合，最重要的是，需要改进其特征学习能力。为了解决这些问题，我们提出了整流局部相位体积（ReLPV）模块，它是标准3D卷积层的有效替代方案。所述ReLPV 块提取相在3D局部邻域（例如，\(3×3×3\)）输入图的每个位置以获得特征图。通过在每个位置的3D局部邻域中的多个固定低频点处计算3D短期傅里叶变换（STFT）来提取相位。然后，在通过激活函数之后，在不同频率点处的这些特征图被线性组合。所述ReLPV块提供至少，显著参数节约\(3^3\) 至\(13^3\)相对于标准三维卷积层倍与滤波器尺寸\(3×3×3\)至\(13\times 13\times 13\)分别。我们展示了ReLPV的特色学习功能块明显优于标准3D卷积层。此外，它在不同的3D数据表示中产生始终如一的更好结果。我们在体积ModelNet10和ModelNet40数据集实现国家的theart准确性，同时利用只有11％的电流了最先进的参数theart。我们还将UCF-101 split-1动作识别数据集的最新技术水平提高了5.68％（从头开始训练时），同时仅使用最先进技术的15％参数。项目网页位于https://sites.google.com/view/lp-3dcnn/home。

1. 简介

在过去的几年中，2D CNN 领域的研究已经导致了许多计算机视觉任务的前所未有的进步，例如图像分类，语义分割和图像超分辨率。除了性能结果之外，2D CNN在其他互补领域也取得了很好的进展，例如网络压缩，二值化，量化，正则化等。不幸的是，与2D对手不同，3D CNN在问题上并没有达到相同水平的性能跳跃。在他们的领域，例如，视频分类和上述补充领域的进展。最近的作品如[ 45 ]和[ 11 ]，列出深度3D CNN建模和训练中的一些基本障碍，例如（1）它们在计算上非常昂贵，（2）它们在内存使用和磁盘空间方面都会导致大型模型（3）由于大量参数，它们易于过度拟合，（4）并且需要改进它们的特征学习能力，这可能需要对其网络架构或标准3D卷积层进行根本改变。尽管存在上述挑战，但深度3D CNN的文献中的当前趋势是训练计算昂贵，存储器密集且非常深的网络以便实现最先进的结果。
在这项工作中，我们通过提出3D CNN的基本构建模块（3D卷积层）的替代方案来绕道这一趋势，3D卷积层是3D CNN中高时空复杂性的主要来源。更确切地说，我们提出了整流局部相位体积（ReLPV）模块，这是3D CNN中标准3D卷积层的有效替代方案。所述ReLPV块包括局部相位模块，所述的RELU激活函数和一组可训练线性权重。局部相位模块通过在局部\(n × n × n\)中计算3D短期傅立叶变换（STFT）（在多个低频点处）来提取局部相位信息 （例如，\(3×3×3\)）输入特征图的每个位置的邻域/体积。然后，本地相模块的输出通过ReLU 激活功能，以便获得固定低频点处的本地相位信息的激活响应图。最后，一组可训练的线性权重计算这些激活的响应图的加权组合。所述ReLPV块提供显著参数与节省计算和存储积蓄沿。基于ReLPV 块的 3D CNN具有低得多的模型复杂性并且不易过度拟合。
最重要的是，其功能学习功能明显优于标准3D卷积层。我们在这项工作中的主要贡献如下：

• 我们提出了ReLPV 模块，它是标准3D卷积层的有效替代方案。所述ReLPV块显著降低可训练参数的数量，与标准相比至少降低了\(3^3\)至\(13^3\)倍，三维卷积层与过滤器尺寸分别\(3×3×3\)至\(13×13×13\)。
• 我们展示了ReLPV模块在不同的3D数据表示上实现了始终如一的更好结果。我们展示这对体积ModelNet10和ModelNet40数据集通过实现只用11％的电流了最先进的参数国家的theart准确性theart。此外，我们提供了时空图像序列的结果。特别是，在 UCF-101分裂1动作识别数据集上，使用最先进的15％参数，将当前的最新技术水平提高了5.68％。
• 我们通过改变其各种超参数来提出所提出的ReLPV块的详细消融和性能研究。该分析将有利于将来设计基于ReLPV块的3D CNN。

2. 相关工作

近年来，二维CNNs在大多数计算机视觉问题中取得了最新的研究成果。此外，它们在网络压缩、二值化、量化、正则化等互补领域也取得了显著进展。因此，将这一成功扩展到三维CNNs领域的问题也就不足为奇了，如视频分类、三维物体识别、MRI体积分割等。不幸的是，3Dcnn在计算上非常昂贵，并且需要很大的内存和磁盘空间。此外，由于涉及大量参数，它们很容易超拟合。因此，最近人们对更有效的3D CNNs变体产生了兴趣。
受二维CNNs网络二值化技术进步的启发，如BinaryConnect、BinaryNet、XNORNet等，Ma等人在中引入了BVCNNs，在BVCNNs中，他们将一些用于从ModelNet数据集中识别体素化三维CAD模型的最先进的3D CNN模型进行了完全的二值化。与浮点基线相比，3D CNNs的二进制版本节省了大量的计算和内存需求。然而，这是以性能降低为代价的。此外，二值化网络仅接受二值化输入，限制了其在视频分类等其他三维数据表示方面的应用。
另一种降低三维神经网络模型复杂度的方法是用可分离卷积代替三维卷积。近年来，许多针对视频分类任务而提出的三维CNN结构都在探索这种技术。可分卷积的概念是先在二维空间上卷积，然后在一维时间上卷积。这种分解在本质上类似于中使用的深度可分离卷积，只是这里的思想是将其应用于时间维度而不是特征维度。这一思想在最近的许多工作中得到了应用，包括R(2+1)D网络、可分离的3D CNNs、伪3D网络和因式时空CNNs。基于可分卷积思想的三维神经网络在时空复杂度较低的情况下，在视频分类任务上取得了与目前最先进的神经网络相比较的竞争效果。

3. 方法

符号。我们用张量\(I∈R^{c\times d\times h\times w}\)表示三维CNN网络中某一层输出的feature map，其中\(h\)、\(w\)、\(d\)和\(c\)分别是feature map的高度、宽度、深度和通道数。
ReLPV块架构。ReLPV块是标准3D卷积层的四层替代表示。图1说明了ReLPV块的结构。

图1: The ReLPV block architecture.

Layer 1。这一层是标准的三维卷积层，只有一个大小为\(1\times 1\times 1\)的过滤器。从上一层输入一个大小为\(c\times d\times h\times w\)的feature map，并将其转换为一个大小为\(1\times d\times h\times w\)的单通道feature map。这一层为第2层计算的3D STFT操作准备输入。设\(f(x)\)为第1层的feature map输出，大小为\(1\times d\times h\times w\)。这里，x是一个变量，表示feature map \(f(x)\)上的位置。

Layer 2。将局部相位成功地应用于图像边缘检测和轮廓提取的特征提取中。相位表示不同空间频率的局部相干性。图像中的边缘和骨架由它们的相干性来表达，在图像理解中起着重要的作用。同样的属性也适用于3D数据表示。例如,视频。在多维中提取局部相位的方法有很多。我们的方法灵感来自。第2层通过公式1计算f(x)在局部\(n\times n \times n\)邻域\(N_x\)的每个位置处的三维短时傅里叶变换(STFT)，提取\(f(x)\)的局部相位谱。
\[
F(v,x)=\sum^{}_{y \in N_x}{f(x-y)exp^{-j2 \pi v^Ty}}
\tag{1}
\]
这里，\(v \in R^3\)是一个频率变量，\(j=\sqrt{-1}\)。使用向量符号[20]，我们可以重写方程1，如方程2所示。
\[
F(v,x)=w^T_v f_x
\tag{2}
\]
其中，\(w_v\)为频率变量v处三维STFT的基向量，\(f_x\)为包含邻域\(N_x\)所有位置的向量。注意，由于基函数的可分性，可以对\(f(x)\)中的所有位置使用简单的一维卷积有效地计算出三维STFT。在这项工作中，我们考虑了13个最低的非零频率变量，定义如下。所选频率变量如图2所示为红点。

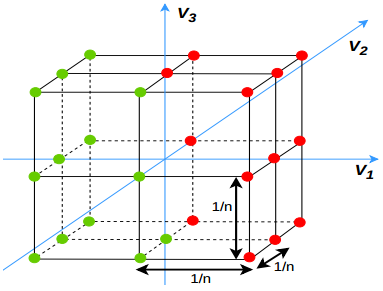
图2:用于计算3DSTFT的频率点。选择的频率点被标记为红点。在绿点的另一个频率点被忽略,因为它们是选定的复杂共轭。

使用低频变量是因为它们通常包含大部分信息，因此它们具有比高频分量更好的信噪比。

让
\[
W=[R\{w_{v_1},w_{v_2},...,w_{v_{13}}\},\zeta\{w_{v_1},w_{v_2},...,w_{v_{13}}\}]^T
\tag{3}
\]
这里W是一个\(26\times n^3\)的变换矩阵对应于13个频率变量。\(R\{·\}\)和\(\zeta\{·\}\)分别返回复数的实部和虚部。因此，由式2和式3可知，13个频率点\((v_1,v_2,…,v_{13})\)的三维STFT矢量形式如式4所示。
\[
F_x=Wf_x
\tag{4}
\]
由于\(F_x\)是对输入\(f(x)\)的所有位置\(x\)进行计算，得到的输出特征图大小为\(26×d×h×w\)。第2层的更详细的数学公式载于A节。

Layer 3。将非线性应用于本地相位信息使网络能够学习复杂的表示。该层通过使用激活函数创建从第2层获得的特征映射的激活响应图。我们使用ReLU激活功能来提高效率和收敛速度。

Layer 4。这一层是标准的三维卷积层,它的大小为\(1\times 1\times 1\)的标准三维卷积层,从第3层得到一个大小\(26\times d\times h\times w\)的特征图,输出一个大小为\(f\times d\times h\times w\)的特征图。请注意,第1层和第4层在3D CNN的训练阶段学习。

我们将使用符号\(ReLPV(n,f)\)作为\(ReLPV\)块，其中\(n\)和\(f\)是其超参数。这里\(n\)表示来自层2的局部3D邻域的大小，\(f\)是层4中使用的\(1×1×1\)滤波器的数量。
使用STFT和本地阶段的重要性。 Hinman等人首次研究了多维空间中的STFT。在[15]中作为图像编码的有效工具。它有两个重要的特性使它对我们的目的有用：（1）自然图像通常由具有尖锐边缘特征的物体组成。已经观察到傅里叶相位信息准确地表示这些边缘特征。由于3D空间中的STFT只是一个窗口傅里叶变换，因此适用相同的属性。因此，本地相位能够以与卷积滤波器相同的方式精确地捕获局部特征。 （2）STFT对输入信号进行去相关。正则化是深度学习的关键，因为它允许训练更复杂的模型，同时保持较低的过度拟合水平并实现更好的泛化。特征，表示和隐藏激活的去相关已成为深度神经网络更好正则化研究的一个活跃领域，提出了各种新的正则化因子，如DeCov，去相关批量归一化（DBN），结构化去相关约束（SDC）和OrthoReg。由于STFT对输入表示进行去相关，并且由于可学习参数的数量减少，基于\(ReLPV\)块的3D CNN不太容易过度拟合并且更好地推广。
在\(ReLPV\)块中向前向后传播。用\(ReLPV\)块代替标准的三维卷积层对三维\(CNN\)网络进行端到端训练是很简单的。通过\(ReLPV\)块的第1层、第3层和第4层向前和向后传播的步骤是所有深度学习库中的标准操作。在第2层中反向传播类似于在没有可学习参数(如加法、乘法等)的情况下通过层传播梯度，因为它涉及到将固定基矩阵W应用于输入。注意，在训练期间，只有第1层和第4层中的\(1\times 1\times 1\)过滤器被更新，而矩阵W中的权重不受影响。
\(ReLPV\)块参数分析。与具有相同滤波器大小/体积和输入-输出通道数量的标准三维卷积层相比，\(ReLPV\)块使用的可训练参数明显较少。考虑一个具有c输入和f输出通道的标准3D卷积层。设\(n\times n\times n\)为滤波器的大小/体积。因此，标准三维卷积层中可训练参数的总数为\(c\times n^3\times f\)。一个包含\(c\)输入通道和f输出通道的\(ReLPV\)块由\(c\times 1+f\times 26\)个可训练参数组成。因此，计算标准三维卷积层中可训练参数个数与所提出的\(ReLPV\)块的比值如下:
\[
\frac{\#\ params.\ in\ 3D\ conv.\ layer}{\#\ params.\ in\ ReLPV\ block}=
\frac{c \cdot n^3 \cdot f}{c \cdot 1 + f \cdot 26}
\tag{5}
\]
为简便起见，我们假设\(f=c\)，即，输入通道和输出通道的数目相同。此外，在实际应用中，大多数深度三维CNNs \(f>=27\)。因此,让\(f = 27\)。这就把上面的比例降低到\(n^3\)。因此，对于标准3D卷积层中大小为\(3 \times 3 \times 3\)的滤波器，\(ReLPV\)块使用的可训练参数要少27倍。因此，在学习\((3 \times 3 \times 3,5 \times 5 \times 5,7 \times 7 \times 7,9 \times 9 \times 9,11 \times 11 \times 11,13 \times 13 \times 13)\)三维卷积滤波器时，\(ReLPV\)块在数值上至少保存了\((27\ast，125\ast，343\ast，729\ast，1331\ast，2197\ast)\)个参数。

4 实验

在本节中，我们展示了与标准的三维卷积层相比，所提出的\(ReLPV\)块在不同的三维数据表示上产生了一致的更好的结果。我们在体素化的三维CAD模型和时空图像序列上演示了这一点。

4.1 三维CAD模型数据集的实验与结果

ModelNet是一个大型的三维CAD模型(形状)库。具有4,899个形状的ModelNet10 (train: 3991, test: 908)和具有12,311个形状的ModelNet40 (train: 9843, test: 2468)通常用作基准数据集，分别包含10和40个类别。每个模型都对齐到一个标准帧，然后围绕z轴以12和24个均匀采样的方向旋转(\(Az\times 12\)和\(Az\times 24\)增强)。然后将这些旋转的模型体素化为\(32\times 32\times 32\)的网格。我们使用了的体素化版本。这里的任务是将给定的体素化三维模型划分为相应的类。

4.1.1 ModelNet:与基线的比较

Baselines。我们首先在基线网络VoxNet、VoxNetPlus和LightNet中，将标准的三维卷积层替换为建议的ReLPV块(带有跳过连接)，并分别将这些新网络称为LP-VoxNet、LP-VoxNetPlus和LP-LightNet。这里LP代表局部相位。用ReLPV块直接替换标准的3D卷积层。例如，VoxNet网络具有如下架构:conv3D(5,32,2)-conv3D(3,32,1)- mp (2)-FC(128)- FC(K)。这里，conv3D(n,f,s)是标准的三维卷积层，带有f个大小为nnn的滤波器，每个滤波器都使用stride s。MP表示最大池化。FC代表全连接层。K是类的数量。VoxNet的等效局部相位版本是:ReLPV(5,32,2)-ReLPV(3,32,1)-MP(2)-FC(128)-FC(K)。在前面关于ReLPV块架构的讨论中，我们只关注重要的超参数，而没有讨论标准3D conv层中常用的其他超参数，比如stride信息。这些信息可以很容易地集成到ReLPV体系结构中。在准备LP-VoxNetPlus和LP-LightNet网络时也遵循类似的步骤。
训练。 我们使用SGD作为优化器训练这些新网络，动量为0.9，分类交叉熵为损失。 在培训期间，我们从学习率为0.008开始，如果验证损失稳定，我们将学习率降低2倍。对于LP-VoxNet和LP-VoxNetPlus网络，在[2625]之后，我们首先在ModelNet40上训练它们，然后在ModelNet10上进行微调。在LPLightNet网络上执行相反的操作，就像在中一样。在[262550]之后，所有网络都针对每个实例围绕z轴的12个均匀采样旋转(\(Az\times 12\)增强)进行训练。测试数据未做数据扩充。

结果。表1列出了新网络与其相应基线的比较。 我们还将新网络与基线的二值化版本进行比较（如第2节所述）。 本地阶段版本明显优于ModelNet10和ModelNet40数据集上的相应基线及其二值化版本。

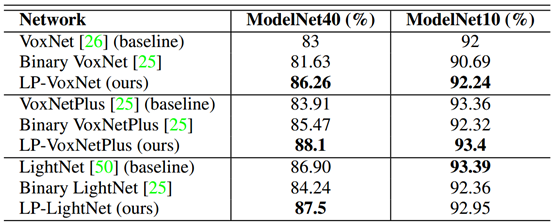
表1:基线网络与本地阶段和二进制版本的比较。本地阶段版本的性能优于基线及其二进制版本。

4.1.2 ModelNet：与最先进的技术进行比较

网络体系结构。我们遵循了[2]的Voxception-ResNet (VRN)体系结构的思想，该体系结构采用简单的inception风格的体系结构和resnet风格的跳过连接。这种设计背后的直觉是，要让信息在网络中流动，有尽可能多的可能路径。对于输入层之后的第一个非下采样块（图3a），我们连接两个具有不同局部相位体积大小（\(3 \times 3 \times 3\)和\(5 \times 5 \times 5\)）的ReLPV块的相同数量（128）的特征图。对于其他非下采样块，我们使用额外的\(1 \times 1 \times 1\)卷积层扩充上述结构，该卷输出与ReLPV块相同数量（128）的特征图，并将其与其他特征图连接，如图3b所示。该架构允许网络在对前一层中的特征图的加权平均（即，通过对\(1 \times 1 \times 1\)卷积进行大量加权）或者关注本地相位信息（即，通过对ReLPV块进行大量加权）之间进行选择。与此同时，如图3b所示，添加跳过连接，以使梯度更平滑地流向先前的层。对于下采样，我们使用具有池大小2和步幅2的平均池。我们的最终模型在图3c中示出，具有五个非下采样块，接着是两个完全连接的层，每个具有512的大小，并且最终的softmax层用于分类。所有非下采样层（在批量标准化之后）和完全连接的层之后是ReLU激活功能。在最终的非下采样层之后使用层conv3D（1, 256）以减少完全连接的层中的参数的数量。

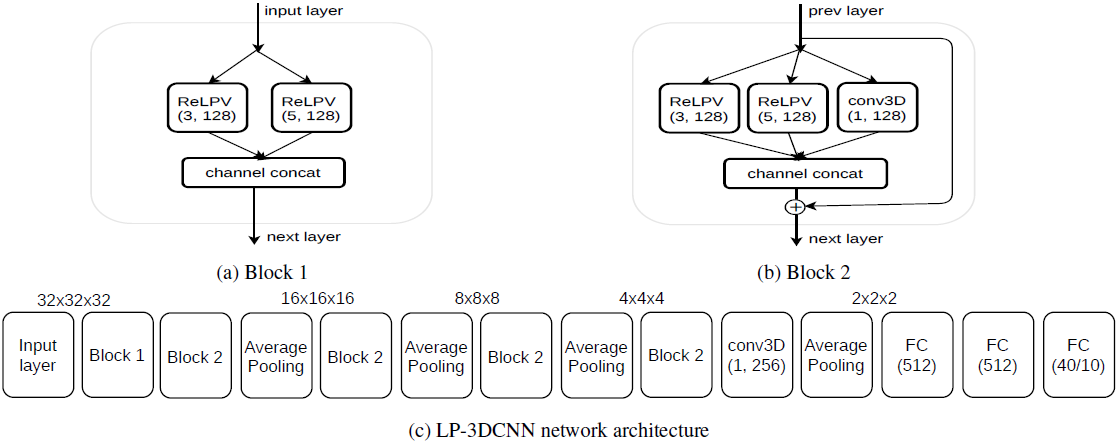
图3:实验和与最新技术的比较。LP-3DCNN网络构建模块及架构。

训练和测试。我们网络的输入是ModelNet数据集中大小为\(32 \times 32 \times 32\)的体素。 在[2]之后，我们将二进制体素范围从{0,1}更改为{-1,5}，以鼓励网络更多地关注正数条目。 使用SGD作为优化器训练网络，动量为0.9，分类交叉熵为损失。 在培训期间，我们从学习率0.008开始，如果验证损失稳定，则将其减少5倍。 使用正交初始化初始化所有权重。 首先在\(Az \times 12\)增强数据上训练网络，然后以低学习速率对\(Az \times 24\)增强数据进行微调。 没有对测试数据进行数据扩充。 除了旋转之外，通过在每个训练示例中添加噪声，随机平移和水平翻转来增强数据，如[26,2]中所做的那样。
结果。表2将我们的结果与使用体素化/体积ModelNet数据集作为输入的其他方法进行了比较。 为了进行公平的比较，我们只考虑这项工作中的体积网络框架。 我们不包括多视图网络或基于点云的网络。 在单一网络框架中，我们提出的网络优于ModelNet10和ModelNet40数据集上的所有先前网络。此外，它只使用了200万个参数，而目前最先进的VRN网络使用了1800万个参数。在集成框架中，VRN在ModelNet10和ModelNet40数据集上都实现了最佳性能。然而，它拥有最复杂的网络架构，多达45层，1.08亿个参数，需要近6天的时间来训练。在集成框架中，我们的网络优于FusionNet，同时使用的参数减少了近59倍，数据增量显着减少。

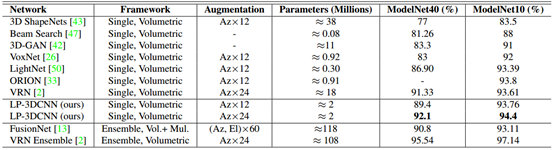
表2：ModelNet数据集的性能结果。 Az代表方位旋转，El代表仰角旋转。 “ - ”表示没有为论文中的项目提供信息。Vol代表体积。Mul代表多视点。

4.2 时空图像序列的实验和结果

数据集。我们使用UCF-101 split-1动作识别数据集[34]。该数据集在[37,38,8]中被用作性能研究的基准数据集，用于搜索用于动作识别任务的3D CNN网络架构和超参数。
基线。我们使用[37]提出的实验性3D CNN网络将动作识别作为基线，这是C3D网络的较小版本[37]。 为简单起见，我们将此网络称为迷你C3D网络或mC3D。 具有表示为\(mC3D_n\)的滤波器大小\(n \times n \times n\)的mC3D网络具有以下架构：conv3D(n, 64)-MP(2)-conv3D(n, 128)-MP(2)-conv3D(n, 256)-MP(2)-conv3D(N, 256)-MP(2)-conv3D(N, 256)-MP(2)-FC(2048)-FC(2048)-FC(101)。每个3D卷积和完全连接的层之后是ReLU激活功能。 所有卷积层都应用适当的填充和步幅1，使得张量的大小从这些层的输入到输出没有变化。 在[37]之后，网络的输入是尺寸为\(3 \times 16 \times 112 \times 112\)的视频。
上述网络的等效局部相位版本，记作\(LP-mC3Dn\)，用ReLPV块替换标准的三维卷积层，如4.1.1所示。这里，n表示计算STFT的局部三维邻域的大小。
训练。在[37]之后，我们使用SGD作为Nesterov动量的优化器，其值为0.9，并且分类的交叉熵为损失。我们训练网络16个时期，学习率为0.003，每4个时期后减少10倍。请注意，所有网络都是从头开始训练的。不使用诸如帧转换，旋转或缩放之类的数据扩充。我们重新训练了所有基线网络（n = 3; 5; 7）。结果发现与[37]中的图2一致。
结果。诸如[37,22]等早期作品表明，在UCF-101 split-1数据集上从头开始训练相对较浅的3D CNN可实现41-44％的性能。 最近的作品如[38,8]使用深度3D残差ConvNet架构来获得更好的结果。 表3报告了我们在UCF-101 split-1数据集上的结果。 我们使用五个ReLPV块，将现有技术提高了5.68％。 与3D STC-ResNet 101网络相比，我们的网络使用了1300万个参数[8]，该网络建立在3D ResNet 101网络的顶层，使用了超过8600万个参数。 此外，具有不同局部相位体积的所有本地相位版本明显优于相应的基线网络。

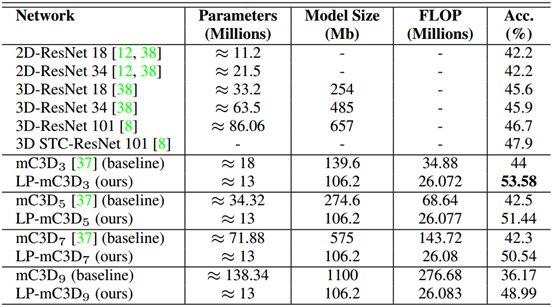
表3:UCF-101 split-1动作识别数据集的性能结果。基于ReLPV块的三维CNNs与相应基线及其他先进网络的比较。所有的网络都是从零开始训练的。

5. 讨论与分析

在本节中，我们详细介绍了RELPV块的烧蚀和性能研究。此外，我们还讨论了RELPV块相对于标准三维卷积层所具有的一些统计优势。

5.1 ReLPV块的时空复杂度

模型的尺寸。表3显示，与相应的基线相比，基于ReLPV块的三维CNNs使用更少的参数，占用更少的磁盘空间。此外，随着局部相体积(同时保持其他超参数不变)从3增加到9，基于ReLPV块的网络中可训练参数的数量或模型大小没有变化。与此相反，随着滤波器尺寸的增大，基线网络的参数和模型尺寸显著增加。我们相信，在资源受限的环境下，ReLPV块的这一特性将为三维CNNs带来巨大的好处。
计算成本。我们在第3节中讨论了由于基函数的可分性，可以通过对每个维使用简单的一维卷积有效地计算STFT。这种使用可分卷积计算三维STFT的技术节省了巨大的计算成本，并且在第2节中讨论了3D CNNs中最近的研究热点。表3根据模型的浮点运算数(FLOP)报告了计算成本。与相应基线相比，基于ReLPV块的三维CNN的触发器值更小。此外，它们随局部相体积的增加变化很小。然而，对于基线网络，随着过滤器大小从3增加到9，触发器值增加了近8倍。

5.2 ReLPV块的统计优势

如前所述，训练深3D CNN的主要挑战之一是避免过度拟合。 Hara等人最近的一项研究。在[11]中表明，即使是相对较浅的3D CNN，如3D ResNet-18，也会在动作识别数据集（如UCF-101 [34]和HMDB-51 [24]）上显着过度拟合。这部分是由于3D CNN中与2D对应物相比的大量可训练参数，部分原因是大规模3D数据集不可用[3811]。这些是深度3D CNN训练的主要瓶颈。为了抑制过度拟合，已经引入了各种训练方法，例如数据增强，训练浅网络和新型正则化器，例如Dropout [35]，DropConnect [40]和Maxout [10]。虽然已经提出诸如[403510]的正则化器来规范网络的完全连接的层，但是诸如[41935]的最近的工作表明，使网络的卷积层正规化同样重要。我们的ReLPV模块用于代替深3D CNN中的标准3D卷积层，由于其使用明显较少的可训练参数以及由于STFT的去相关特性而自然地使网络正规化（参见第3节）。图4报告了我们对过度拟合实验的结果。与基线\(mC3D_3\)网络相比，\(LP-mC3D_3\)网络明显更容易配置并且明显更好地推广。

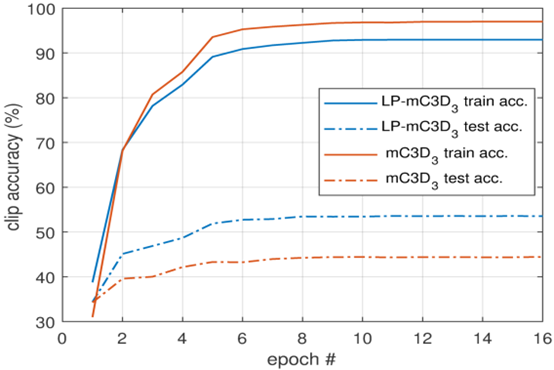
图4:UCF-101 Split-1数据集上的过度拟合结果。与基线\(mc3d_3\)网络相比，\(lp-mc3d_3\)网络的过拟合度更小，通用性更好。

5.3 Exploring the Local Phase Volume of the ReLPV block

如前所述，ReLPV块采用两个超参数作为输入，其中一个是输入特征映射的每个位置计算STFT（并且提取局部相位）的局部体积的大小。 在本节中，我们将探讨这个超参数。 我们尝试了不同大小的局部体积，特别是\(3 \times 3 \times 3\)到\(9 \times 9 \times 9\)。 我们发现ReLPV块的性能随着STFT体积的增加而降低。 图5显示了UCF-101测试分裂-1数据集上\(LP-mC3Dn\)网络的剪辑精度，其中各种STFT体积在16个时期内从\(3 \times 3 \times 3\)到\(9 \times 9 \times 9\)不等。 STFT卷为\(3 \times 3 \times 3\)的\(LP-mC3D_3\)网络表现最佳，而\(LP-mC3D9\)网络表现最差。 注意，在[37]中对标准3D卷积层进行了类似的研究，其中发现在所有层中具有\(3 \times 3 \times 3\)卷积核的3D CNN表现最佳。

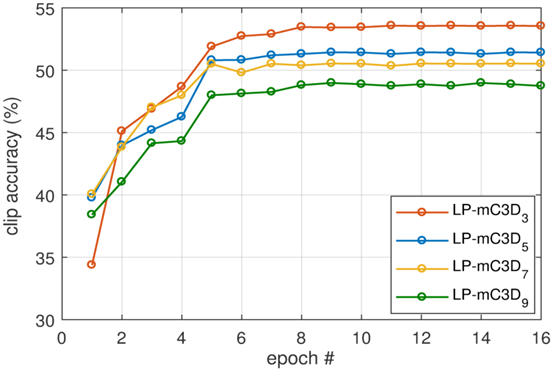
图5:ReLPV块STFT卷搜索。STFT体积为\(3\times 3\times3\)的\(LP-mC3D_3\)网络性能最好。

5.4 研究由ReLPV块输出的特征映射的数量

在本节中，我们将探索另一个超参数，即ReLPV块输出的特征映射的数量。简单来说，我们探索了在ReLPV块的第4层中改变\(1 \times 1 \times 1\)滤波器数量的效果(参见第3节)。为此，我们使用\(LP-mC3Dn\)网络的修改版本，并试验不同的ReLPV块超参数对(n, f)。设\(LP-mC3D_{(n, f)}\)为我们的实验网络，具有以下架构：输入层-\(ReLPV(n, f)\)-\(MP(2)\)-\(ReLPV(n, f)\)-\(MP(2)\)-\(ReLPV(n, f) )\)-\(MP(2)\)-\(ReLPV(n, f)\)-\(MP(2)\)-\(ReLPV(n, f)\)-\(conv3D(1 \times 1 \times 1, 256)\)-\(MP(2)\)-\(FC(2048)\)-\(FC(2048)\)-\(FC(101)\)。在最后一个\(ReLPV\)块之后使用层\(Conv3D(1 \times 1 \times 1, 256)\)，以便完全连接层中的参数数量不会在不同网络之间变化。表4显示了我们在UCF-101 split-1测试集上的实验结果。我们观察到，对于局部STFT体积的固定值(超参数n)，性能随着\(1 \times 1 \times 1\)滤波器(超参数f)的数量的增加而提高。另一个重要的观察是模型大小和可训练参数的数量随着超参数f的值的增加而变化非常小。

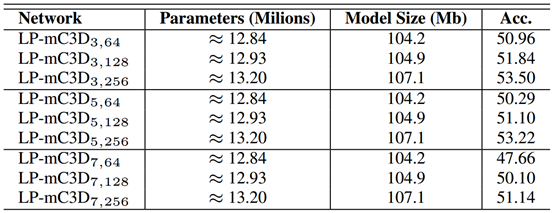
表4:研究ReLPV块输出的feature map的数量。性能随着f值的增加而提高。

5.5 基于ReLPV块的混合3D CNN模型

在本节中，我们将探讨在单个3D CNN网络中使用ReLPV块和标准3D卷积层的性能影响。我们称这种网络为混合3D CNN。我们尝试了两种类型的变体。在第一个变体中，我们用ReLPV块替换传统3D CNN网络（基线\(mC3D_3\)）的前几个层（顶层）（在输入层之后），使得由ReLPV块学习的特征图输入到后面的标准3D卷积层。 。在第二变型中，后几层（底层）被ReLPV块替换，使得由标准3D卷积层学习的特征图被输入到后面的ReLPV块。我们使用符号\(mC3D_3\)（\(B_l = T_l\)）来表示\(mC3D_3\)的l个底部/顶部连续3D conv层被ReLPV块替换。表5报告了我们的实验结果。我们观察到，用传统3D CNN网络顶部的ReLPV块替换标准3D卷积层可以改善其性能，而在底层添加ReLPV块时会发生相反的情况。然而，混合3D CNN的性能并不优于\(LP-mC3D_3\)网络，其中所有层都被ReLPV块替换（表3）。

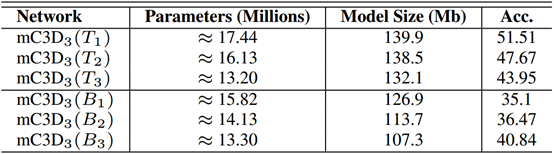
表5:混合3D CNN架构的结果。在UCF-101 split-1测试集上的性能结果。

6. 结论

为了降低传统三维神经网络的高时空复杂度和模型复杂度，本文提出了一种替代标准三维卷积层的有效方法——ReLPV块。在传统的三维神经网络中，使用ReLPV块代替标准的三维卷积层，显著提高了基线结构的性能。此外，它们在不同的3D数据表示之间产生一致的更好的结果。我们提出的基于ReLPV块的三维CNN结构在ModelNet和UCF-101 split-1动作识别数据集上取得了最先进的结果。我们计划将ReLPV block应用到3D CNN架构中，用于其他3D数据表示和3D MRI分割等任务。

A. 第二层详解

设\(f(x)\)为\(ReLPV\)块第1层输出的大小为\(1\times d\times h\times w\)的单通道feature map。其中\(h、w、d\)分别表示feature map的高度、宽度和深度。为了简单起见，我们将删除通道维数，并将\(f(x)\)的大小重写为\(d\times h\times w\)。这里，\(x<Z^3\)是\(f(x)\)中元素的三维坐标。
\(f(x)\)中的每一个\(x\)都有一个\(n\times n\times n\)的三维邻域，用\(N_x\)表示，如式6所示。我们在原稿中提供了详细的实验分析，研究了不同\(n\)对用于视频分类任务的三维CNNs中ReLPV块性能的影响。
\[
N_x=\{ y \in Z^3; ||(x-y)|| \infty \leq r;n=2r+1;r \in Z_+ \}
\tag{6}
\]
对于所有位置\(x = \{ x1,x2,…,x_{d·h·w} \}\)的特征图\(f(x)\)，我们使用局部3D社区,\(f(x - y)\)，\(\forall y \in N_x\)以在方程7中定义的短期傅里叶变换(STFT)推导出局部频域表示。
\[
F(v,x) = \sum^{}_{y_i \in N_x}f(x-y_i)exp^{-j2\pi v^T y_i}
\tag{7}
\]
这里\(i = 1,...,n^3\)，\(v<R^3\)是一个3D频率变量，\(j = \sqrt{-1}\)使用向量符号[20]，我们可以重写方程7，如方程8所示：
\[
F(v,x)=W^T_v f_x
\tag{8}
\]
这里\(w_v\)是一个线性变换的复值基函数(在频率变量\(v\)处)，定义如式9所示。
\[
W^T_v=[exp^{-j2\pi v^T y_1},exp^{-j2\pi v^T y_2},...,exp^{-j2\pi v^T y_3}]
\tag{9}
\]
\(f_x\)是一个包含邻域\(N_x\)中所有元素的向量，定义如式10所示。
\[
f_x=[f(x-y_1),f(x-y_2),...,f(x-y_{n^3})]^T
\tag{10}
\]
在我们的工作中，我们考虑了13个最低的非零频率变量\(v_1,v_2…v_{13}\)。使用低频变量是因为它们通常包含大部分信息，因此它们比高频分量[14]具有更好的信噪比(见B节)。由式8定义上述频率变量的局部频域表示如式11所示。
\[
F_x=[F(v_1,x),F(v_2,x),...,F(v_{13},x)]^T
\tag{11}
\]
在每个位置\(x\)，将每个分量的实部和虚部分离后，得到一个向量，如式12所示。
\[
F_x=[R\{F(v_1,x)\},\zeta \{F(v_1,x)\},R\{F(v_2,x)\},\zeta \{F(v_2,x)\},...,R\{F(v_{13},x)\},\zeta \{F(v_{13},x)\}]^T
\tag{12}
\]
这里\(R\{\cdot \}\)和\(\zeta\{\cdot \}\)分别返回复数的实部和虚部。对应的\(26\times n^3\)变换矩阵如式13所示。
\[
W=[R\{W_{v_1}\},\zeta\{w_{v_1}\},...,R\{W_{v_{13}}\},\zeta\{w_{v_{13}}\}]^T
\tag{13}
\]
由式8和式13可知，所有13个频率点例如\(v_1,v_2,...,v_{13}\)的STFT矢量形式可以写成如式14所示。
\[
F_x=Wf_x
\tag{14}
\]
由于\(F_x\)是对输入\(f(x)\)的所有位置\(x\)进行计算，得到的输出feature map大小为\(26\times d \times h \times w\)，然后将该feature map作为输入传递给\(ReLPV\) block的Layer 3。

B. STFT的去相关性质及低频变量选择的原因

正如在原稿中提到的，短时傅里叶变换(STFT)的一些重要特性是它能够去关联输入信号并压缩信号中包含的能量(信息)。这些性质是STFT固有的，因为它属于正交变换家族，如K-L变换、Walsh-Hadamard变换(WHT)和离散余弦变换(DCT)。上述所有正交变换都具有以下共同的性质。

• 正交变换具有去相关输入信号[41]的趋势。例如，考虑一个包含温度作为时间函数的信号。现在，给定信号当前样本的值，可以有合理的信心预测其下一个样本的值与当前样本接近，即，两个连续时间样本高度相关。另一方面，经过正交变换(如傅里叶变换)后，知道某个频率分量的大小，就对下一个频率分量的大小(或能量)几乎没有概念，即，与变换前的时间样本相比，这两个分量的相关性要小得多。同样的特性也适用于多个维度的信号，比如图像和视频。在图像和视频中，由于STFT对图像和视频的相关系数不敏感，导致去相关。
• 正交变换倾向于将信号中包含的能量(信息)压缩成少量的信号分量。例如，傅里叶变换后，大部分能量(信息)将集中在相对较少的低频分量上。大多数高频分量携带的能量很少。此外，低频分量比高频分量具有更好的信噪比。正因为如此，我们在计算STFT时选择了低频变量。