Closest Common Ancestors (Lca,tarjan)

午时刷题，难甚，遂小憩于桌上，惊醒，于梦中有所得，虽大声曰：吾已得tarjan之奥秘！

关于tarjan算法，其实就是一个递归加并查集的应用。

大致代码：

#include<bits/stdc++.h>
using namespace std;
int find(int x){
        ....
}

void  join(int x,int y)
{
    ....
}
void dfs(int x)
{
    int len=v[x].size();
    for(int i=; i<len; i++)      //遍历x的子节点
    {
        dfs(v[x][i]);           //继续往下推
        join(v[x][i],x);        //将x的所有子节点的祖先都设为x
    }
    vis[x] = true;              //证明x走过了
    for(int i=; i<=n; i++)         //对每个x循环1~n
        if(vis[i]&&g[x][i])       //如果i已经走过并且要求(x,i)
            ans=find(i);       //lca就是ans
}

由以上代码可以看出，tarjan实际上就是并查集与dfs的结合，其最核心的部分就是dfs那部分

只要理解了dfs()的内容，就能理解tarjan

而对于dfs函数，我们首先就会想到它的特性：不撞南墙不回头。

假如有一颗树，对其dfs，那么首先它会沿着一个分支一直到尽头(如图)：

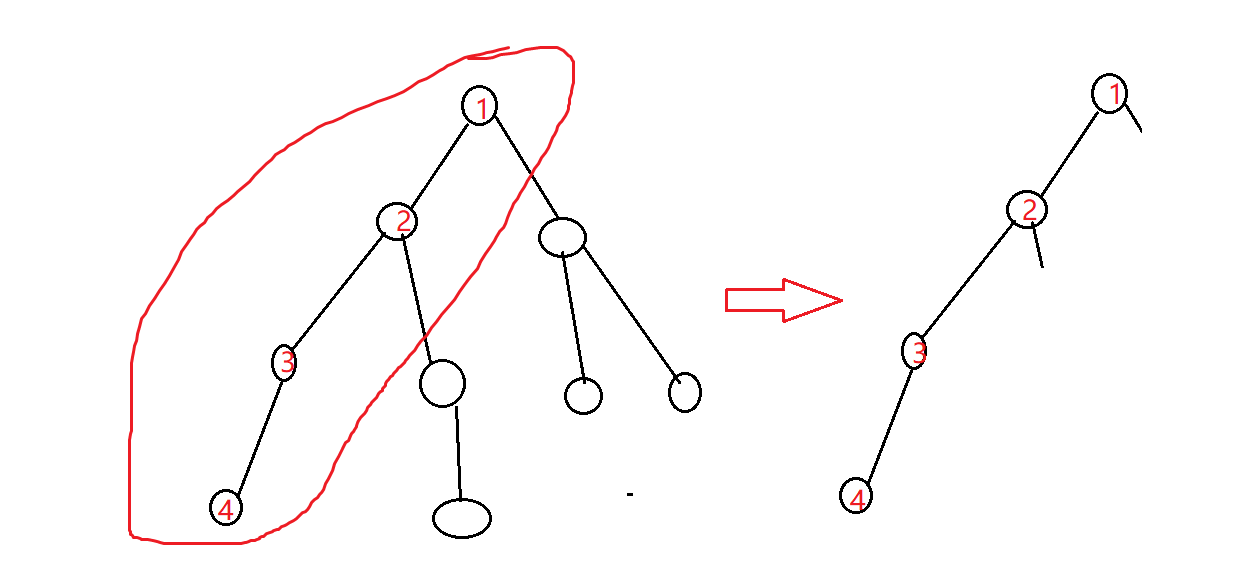
而当走到4这个点时，函数开始执行下列语句：

join(v[x][i],x);        //将x的所有子节点的祖先都设为x 
//而此时pre[4]=3;pre[3]=3;pre[2]=2;pre[1]=1;

再然后是：

 vis[x] = true;              //证明x走过了
    for(int i=1; i<=n; i++)         //对每个x循环1~n
        if(vis[i]&&g[x][i])       //如果i已经走过并且要求(x,i)
            ans=find(i);       //lca就是ans
}
如果存在要求lca[x][i],先看i点是否走过，如果走过，那就只有一种可能(真相只有一个！真実はいつも一つ)：

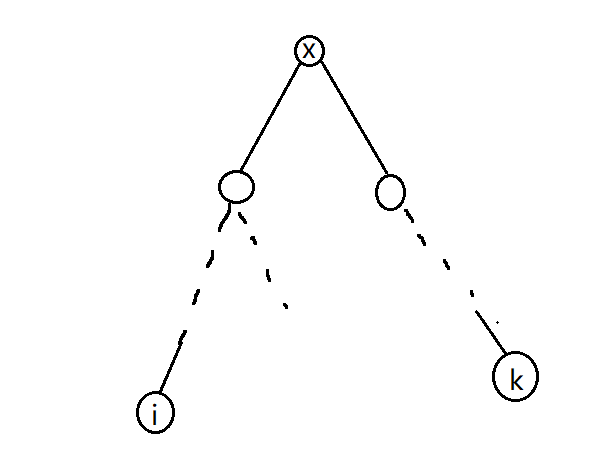
i，k必在两条不同分支上，并且交于某个点x，如果i已经走过了，那么，i所在的这条分支上所有的点都有明确的父子关系，即find(i)==x!
代码参上：

#pragma GCC optimize(2)
#include<stdio.h>
#include<string.h>
#include<vector>
#define M 1007
using namespace std;
int g[M][M],in[M],pre[M],cnt[M];
bool vis[M];
vector<int>v[M];
int n,m;
void init()
{
    memset(g,,sizeof(g));
    memset(in,,sizeof(in));
    memset(cnt,,sizeof(cnt));
    memset(vis,false,sizeof(vis));
    for(int i=; i<=n; i++)
    {
        v[i].clear();
        pre[i]=i;
    }
}
int fond(int x)
{
    return x==pre[x]?x:pre[x]=fond(pre[x]);
}
void join(int x,int y)
{
    int xx=fond(x);
    int yy=fond(y);
    pre[xx]=yy;
}
void dfs(int x)
{
    int len=v[x].size();
    for(int i=; i<len; i++)      //遍历x的子节点
    {
        dfs(v[x][i]);           //继续往下推
        join(v[x][i],x);        //将x的所有子节点的祖先都设为x
    }
    vis[x] = true;              //证明x走过了
    for(int i=; i<=n; i++)         //对每个x循环1~n
        if(vis[i]&&g[x][i])       //如果i已经走过并且要求(x,i)
            cnt[fond(i)]+=g[x][i];  //
}
int main()
{
    while(scanf("%d",&n)!=EOF)
    {
        init();
        int a,b,c,root;
        for(int i=; i<=n; i++)
        {
            scanf("%d:(%d)",&a,&b);
            while(b--)
            {
                scanf(" %d",&c);
                v[a].push_back(c);
                in[c]++;
            }
        }
        scanf("%d",&m);
        getchar();
        while(m--)
        {
            scanf("(%d,%d)",&a,&b);
            getchar();
            g[a][b]++;
            g[b][a]++;
        }
        for(int i=; i<=n; i++)
            if(!in[i])
            {
                root=i;
                break;
            }
        dfs(root);
        for(int i=; i<=n; i++)
        {
            if(cnt[i])
                printf("%d\n",i);
        }
    }
    return ;
}

以上；