2019.6.28 校内测试 T3 【音乐会】道路千万条

大眼一看最下面的题意解释的话，发现这和洛谷P1310表达式的值挺像的，大概都是给定一些运算符号，让最后的表达式为true的概率，为false的概率啥的QwQ~；

然后这个题嘛？就是在所有的运算符中提溜出一个作为最后一次运算的运算符，然后我们去算这个运算符左边的那一堆式子，然后再算右边那一堆式子，最后再算一下最后一个运算符对应的运算就好啦！

那么怎么算这个运算符左边的式子和右边的式子呢？我们再从左边的式子中找出一个运算符最为最后一次运算的运算符，然后算它左边的式子，算它右边的式子……

我们发现这就是一个枚举 + 递归的过程是吧QwQ~

直到我们一直递归到式子长度为1的情况了，这时候如果是' t '那就对应一种表达式为true的情况，如果是' f '那就对应了一种表达式为false的情况；

我们开两个数组 t [ i ][ j ]表示区间 [ i，j ]的表达式为true的方案数，f [ i ][ j ]表示区间 [ i，j ]的表达式为false的方案数，那么有如下边界设置：

    for(int i=;i<=n;i++)
    {
        if(s[i]=='t')               //贡献了一个为true的方案
        {
            t[i][i]=,f[i][i]=;
        }
        else                        //否则就贡献一个为false的方案
        {
            f[i][i]=,t[i][i]=;
        }
    }
//s数组里存的是't' or 'f' 

那么最终的答案就是：

然后 t 和 f 都是遍历区间内所有的运算符，假设作为最后一个运算，根据运算符的规则，递归求左子区间和右子区间的答案，相乘。最后把所有可能的情况累加起来，返回。

就是一个递归的思路，这里用了记忆化的原理，开数组将每种情况的方案数存起来。

但是时间复杂度还是比较高，对于这个题还是会炸！

那么这个题的正解就是：区间DP！

参考我们当时做洛谷P1040 加分二叉树的思路（不知道的先看一下这里）：

我们也是推出了对于每个数字，让它作为根结点，然后算左子树，算右子树，最后再算整体的；这个思路不是和本题很相似嘛？

所以我们仍然可以套上之前我们区间DP的做法：

按照区间长度从小到大开始，枚举每个区间，算出每个区间内表达式为true的方案数，为false的方案数；

利用我们之前求出的小区间，然后一步一步得推出更大区间的答案，最后覆盖整个大区间的答案；

 

先献上区间DP的一般套路：

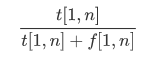
    for(int len=;len<=n;len++)          //枚举区间长度
        for(int i=;i+len-<=n;i++)       //枚举区间左端点的位置
           {
            int j=i+len-;                        //计算出区间右端点的位置
            for(int k=i;k<j;k++)              //枚举区间内的中间点
                ……………
            }

已经确定了要使用区间DP了，接下来的任务就是要找状态转移方程了（下面的过程就和分析P1310表达式的值 的时候几乎一样了）；

题目中只有三种运算符：

与&，或 |，异或 ^，先了解一下它们的运算规则：

&：要使 x&y=1，x和y必须都为1；要使 x&y=0，x和y有一个为0；

| ：要使x | y=1，x和y有一个为1；要使x | y=0，x和y必须都为0；

^：要使x ^ y=1，x和y必须不相同（即x=0，y=1或 x=1，y=0）；要使x ^ y=0，x和y必须相同（即x=0，y=0或 x=1，y=1）；

然后我们就可以根据它们的运算法则来确定状态转移方程啦（还运用了乘法计数原理）：

    for(int len=;len<=n;len++)          //枚举区间长度
    {
        for(int i=;i+len-<=n;i++)      //枚举区间左端点的位置
        {
            int j=i+len-;               //计算出区间右端点的位置
            for(int k=i;k<j;k++)         //枚举区间内的中间点的运算符号
            {
                if(ops[k]=='&')          //&运算
                {
                    t[i][j]=(t[i][j]+(t[i][k]*t[k+][j])%mod)%mod;    //必须两个都为true
                    f[i][j]=(f[i][j]+(t[i][k]*f[k+][j])%mod+(f[i][k]*t[k+][j])%mod+(f[i][k]*f[k+][j])%mod)%mod;  //只需要其中一个为false
                }
                if(ops[k]=='|')          //|运算
                {
                    t[i][j]=(t[i][j]+(t[i][k]*f[k+][j])%mod+(f[i][k]*t[k+][j])%mod+(t[i][k]*t[k+][j])%mod)%mod;  //只需要其中一个为true
                    f[i][j]=(f[i][j]+(f[i][k]*f[k+][j])%mod)%mod;    //必须两个都为false
                }
                if(ops[k]=='^')          //异或运算
                {
                    t[i][j]=(t[i][j]+(t[i][k]*f[k+][j])%mod+(f[i][k]*t[k+][j])%mod)%mod;   //必须两个不同
                    f[i][j]=(f[i][j]+(f[i][k]*f[k+][j])%mod+(t[i][k]*t[k+][j])%mod)%mod;   //必须两个相同
                }
            }
        }
    }

注意到我们的答案是需要取模的，而最后的答案还涉及到了除法，所以最后我们还需要一步求乘法逆元的过程！

这里我用的是扩展欧几里得求逆元，这个大家应该都会吧QwQ~

上代码喽！

#include<bits/stdc++.h>
using namespace std;
inline int read()
{
    int X=,w=;
    char c=getchar();
    while(c<''||c>'')
    {
        if (c=='-')
        {
            w=-;
        }
        c=getchar();
    }
    while(c>=''&&c<='')
    {
        X=(X<<)+(X<<)+c-'';
        c=getchar();
    }
    return X*w;
}
inline char gc()
{
    char c;
    do
    {
        c=getchar();
    }
    while(c==' '||c=='\n'||c=='\r'||c=='\0'||c=='\t');
}
int n;
long long x,y;
char s[],ops[];
long long t[][],f[][];
const int mod=;
void exgcd(long long a,long long b,long long &x,long long &y)   //扩展欧几里得求逆元
{
    if(b==)
    {
        x=;y=;return ;
    }
    exgcd(b,a%b,x,y);
    long long r=x;
    x=y;
    y=r-(a/b)*x;
}
int main()
{
    n=read();
    for(int i=;i<=n-;i++)
    {
        s[i]=gc();         //存't' or 'f'
        ops[i]=gc();       //存运算符
    }
//这么读入的原因是注意到't','f'是和运算符一个一个隔开的
    s[n]=gc();
    for(int i=;i<=n;i++)
    {
        if(s[i]=='t')      //边界条件
        {
            t[i][i]=,f[i][i]=;
        }
        else
        {
            f[i][i]=,t[i][i]=;
        }
    }
    for(int len=;len<=n;len++)          //枚举区间长度
    {
        for(int i=;i+len-<=n;i++)      //枚举区间左端点的位置
        {
            int j=i+len-;               //计算出区间右端点的位置
            for(int k=i;k<j;k++)         //枚举区间内的中间点
            {
                if(ops[k]=='&')          //&运算
                {
                    t[i][j]=(t[i][j]+(t[i][k]*t[k+][j])%mod)%mod;    //必须两个都为true
                    f[i][j]=(f[i][j]+(t[i][k]*f[k+][j])%mod+(f[i][k]*t[k+][j])%mod+(f[i][k]*f[k+][j])%mod)%mod;  //只需要其中一个为false
                }
                if(ops[k]=='|')          //|运算
                {
                    t[i][j]=(t[i][j]+(t[i][k]*f[k+][j])%mod+(f[i][k]*t[k+][j])%mod+(t[i][k]*t[k+][j])%mod)%mod;  //只需要其中一个为true
                    f[i][j]=(f[i][j]+(f[i][k]*f[k+][j])%mod)%mod;    //必须两个都为false
                }
                if(ops[k]=='^')          //异或运算
                {
                    t[i][j]=(t[i][j]+(t[i][k]*f[k+][j])%mod+(f[i][k]*t[k+][j])%mod)%mod;   //必须两个不同
                    f[i][j]=(f[i][j]+(f[i][k]*f[k+][j])%mod+(t[i][k]*t[k+][j])%mod)%mod;   //必须两个相同
                }
            }
        }
    }
    exgcd(t[][n]+f[][n],mod,x,y);
    cout<<t[][n]*((x+mod)%mod)%mod;
    return ;
}