二叉堆的介绍和Java实现

一、堆和二叉堆

堆，英文名称Heap，所谓二叉堆(也有直接称二叉堆为堆的)，本质上是一个完全二叉树，前面也提到过，如果树接近于完全二叉树或者满二叉树，采用顺序存储代价会小一点，因此常见的二叉堆均是顺序实现的。

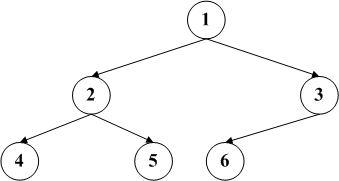
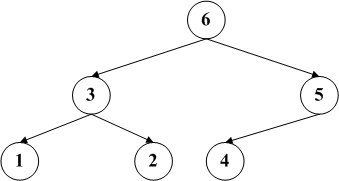
按照排列的顺序可以分为最大堆和最小堆，最大堆的特征是父节点一定大于(依据情况判断是大于等于还是严格大于，数据结构归根到底还是用来使用的)子节点的数据。同样，有最大堆就会有最小堆，最小堆的 父节点数据小于其子节点的数据，因此根节点的数据是最小的。下面左图是一个最小堆，右图是一个最大堆。

    

二、二叉堆的插入和删除

详细来看，二叉堆的主要操作就是插入和删除。以一个最小堆为例，我们详细介绍插入和删除的操作。

    

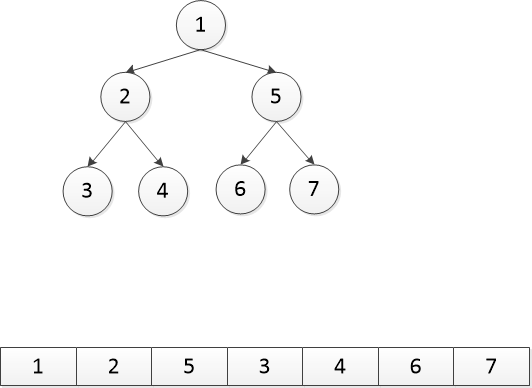
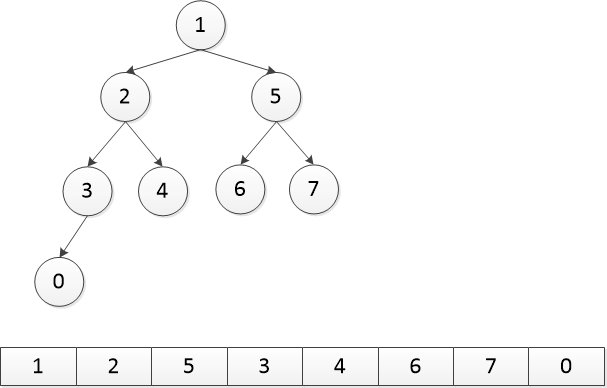
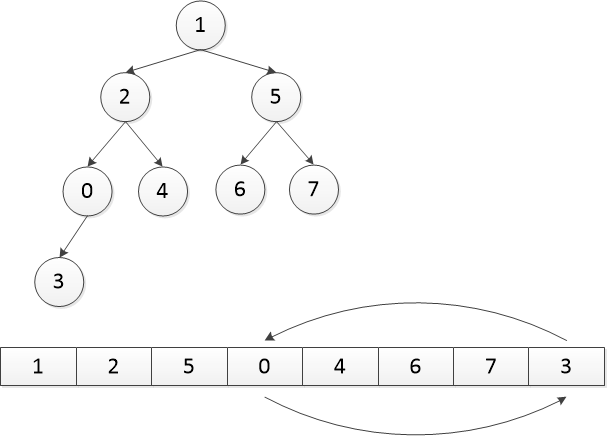
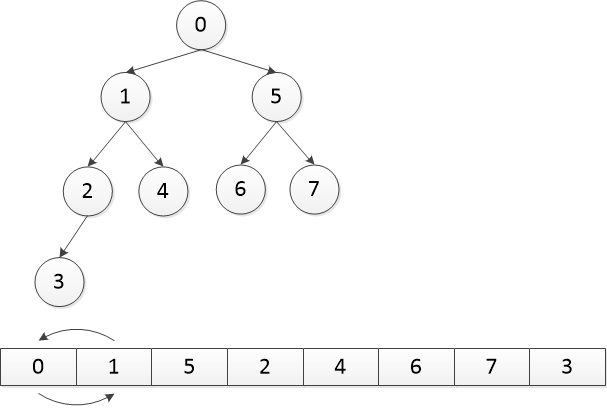
以上是一个最小二叉堆的插入过程，比如我们要插入一个节点0，但是他的数据小于它父节点的数据，因此它和它父节点交换数据，如上面的第三张图所示。然后继续判断，它仍连续两次小于父节点数据，因此再交换两次数据，形成最终的那张图，就是插入后的最小二叉堆。

     

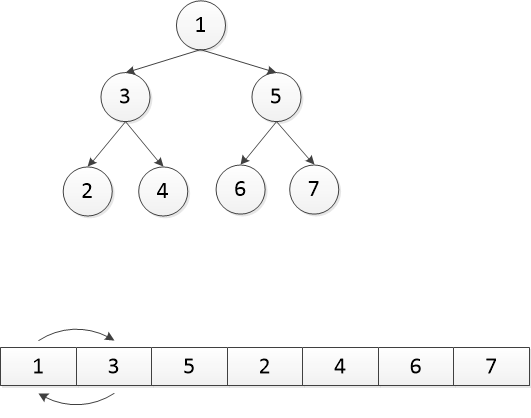
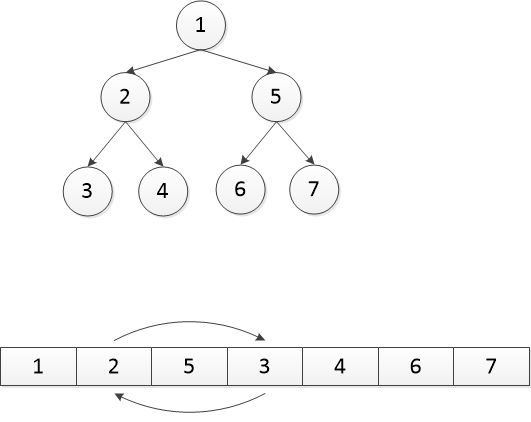
一般来说，二叉堆的删除主要是指删除堆顶的数据，即根节点的数据。我们使用之前插入后得到的二叉堆作为目标，我们对其进行删除操作，假设再次删除节点0，然后将数组中最后一位(节点3)填充进去；然后和子节点的数据进行比较，这时候我们必须要从左右子节点中选出更小的那一个作比较，显然是左节点1较小；如果该节点数据大于子节点(较小的那个)的数据，那就和子节点数据进行交换，直至符合条件；

而查找性的删除则比较复杂，从堆尾补充进删除位置的新数据首先要和父节点的数据进行比较，如果小于，就把该节点一直往上交换，直至停止。但本实例中该节点是根节点，不存在父节点，因此就没有这一步；然后按照上面那一段描述与子节点进行比较，交换。

三、二叉堆的Java实现

成员域由ArrayList<Y> data代表堆中的数据，因为数组无法适配泛型。

插入

    public void insert(Y y)
    {
        data.add(y);
        int index = data.size() - 1;
        while(((index + 1) / 2 - 1) >= 0 && data.get(index).compareTo(data.get((index + 1) / 2 - 1)) < 0)
        {
            Y temp = data.get((index + 1) / 2 - 1);
            data.set((index + 1) / 2 - 1, y);
            data.set(index,temp);
            index = (index + 1) / 2 - 1;
        }
    }

删除

    public boolean delete(Y y)
    {
        if(data.size() == 0)
            return false;
        else if (data.indexOf(y) == -1)
            return false;
        else
        {
            int index = data.indexOf(y);
            data.set(index, data.get(data.size() - 1));
            data.remove(data.size() - 1);

           /* parent */
            while(((index + 1) / 2 - 1) >= 0 && data.get(index).compareTo(data.get((index + 1) / 2 - 1)) < 0)
            {
                Y temp = data.get((index + 1) / 2 - 1);
                data.set((index + 1) / 2 - 1, data.get(index));
                data.set(index,temp);
                index = (index + 1) / 2 - 1;
            }

            /* child */

            while((2 * index + 1) <= data.size()-1)
            {
                if ((2 * index + 2) <= data.size()-1)      //如果该节点左右子树均存在
                {
                    int cmp = data.get(2 * index + 1).compareTo(data.get(2 * index + 2));   //比较子树的大小
                    if (cmp > 0)                  //左子树大于右子树，则交换右子树
                    {
                        if (data.get(index * 2 + 2) .compareTo(data.get(index)) < 0 ) {
                            Y temp = data.get(index * 2 + 2);
                            data.set(index * 2 + 2, data.get(index));
                            data.set(index, temp);
                            index = index * 2 + 2;
                        }
                          else
                          break;
                    }

                    else                       //右子树大于左子树，则交换左子树
                    {
                        if(data.get(index * 2 + 1) .compareTo(data.get(index)) < 0 ) {
                            Y temp = data.get(index * 2 + 1);
                            data.set(index * 2 + 1, data.get(index));
                            data.set(index, temp);
                            index = index * 2 + 1;
                        }
                        else
                        break;
                    }
                }

                else if ((2 * index + 2) > data.size()-1)   //只存在左子树
                {
                    if(data.get(index * 2 + 1) .compareTo(data.get(index)) < 0 ) {     //判断左子树和节点大小
                        Y temp = data.get(index * 2 + 1);
                        data.set(index * 2 + 1, data.get(index));
                        data.set(index, temp);
                        index = index * 2 + 1;
                    }
                    else 
                      break;
                }
            }
            return true;
        }
    }

测试代码1

以此堆为例，插入0后删除0

        Heap <Integer> h = new Heap<>();
        Integer [] i = {1,2,5,3,4,6,7};
        for (int j = 0; j < i.length; j++)
        {
            h.insert(i[j]);
        }

        h.traverse();
        System.out.println();

        h.insert(0);

        h.traverse();
        System.out.println();

        h.delete(0);

        h.traverse();

Test 1

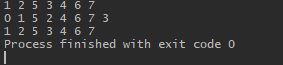
结果1：

————————————————————————————————————————————————————————

测试代码2

        Heap <Integer> h = new Heap<>();
        Integer [] i = {10,20,40,30,60,80,110,50,70,90,100};
        for (int j = 0; j < i.length; j++)
        {
            h.insert(i[j]);
        }

        h.traverse();
        System.out.println();

        h.insert(0);

        h.traverse();
        System.out.println();

        h.delete(0);

        h.traverse();

Test 2

结果2：