2018ccpc吉林 E:THE TOWER——数形结合

题目

链接

给你一个圆锥（位于坐标原点，告诉你高h 和底面半径 r），和一个点（x，y，z）并告诉你这个点的速度，

让你求点和圆锥相撞的最小时间（保证一定相撞）

分析

易知，将直线的参数方程与圆锥曲面的方程联立，但是可能产生增根，具体情形如下：

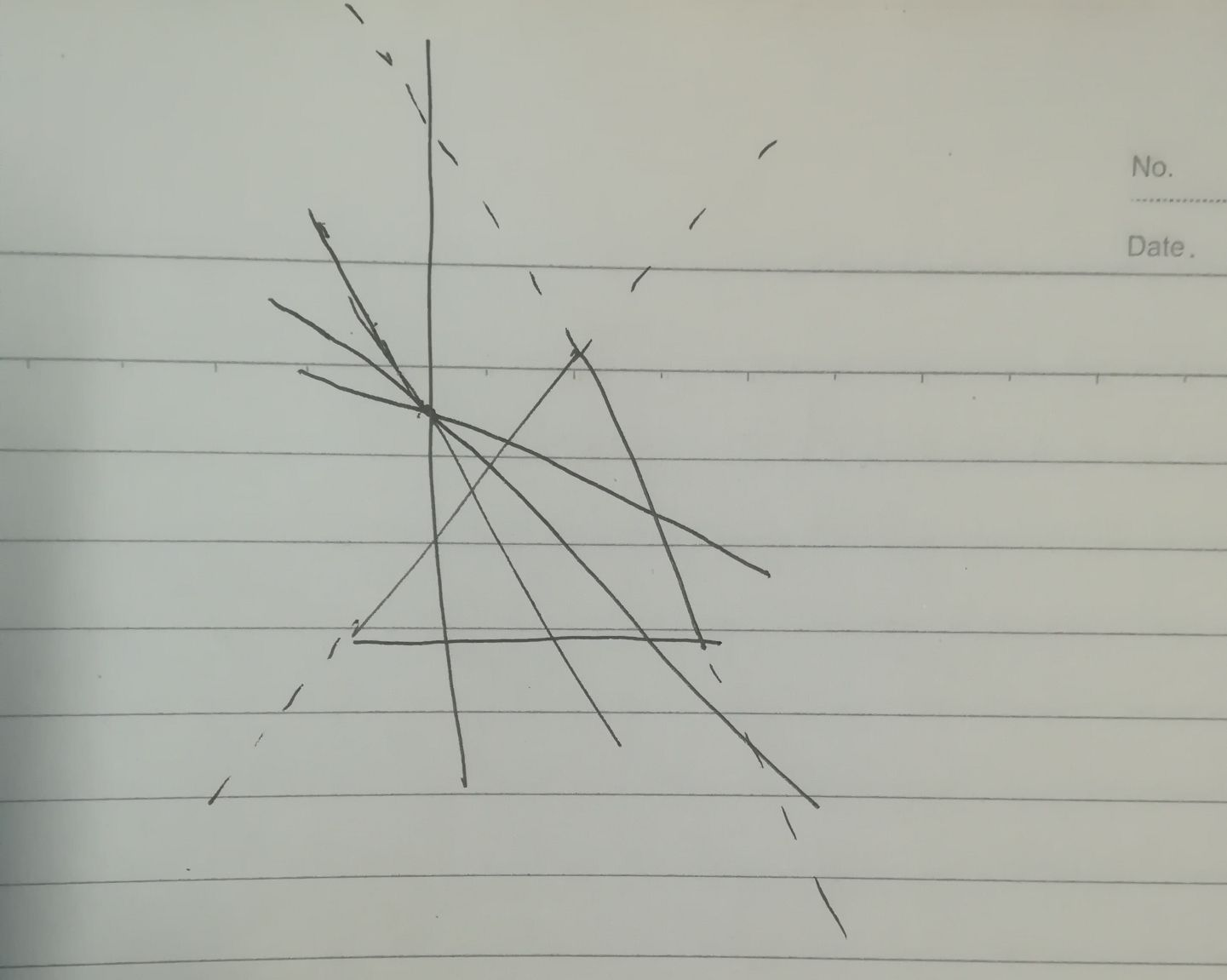
其实我们不必区分具体情况，只需交点在曲面上的时间的最小值。

注意两点，一是判断交点在曲面上不能使用x,y约束，而应该使用z，试考虑如下情况：

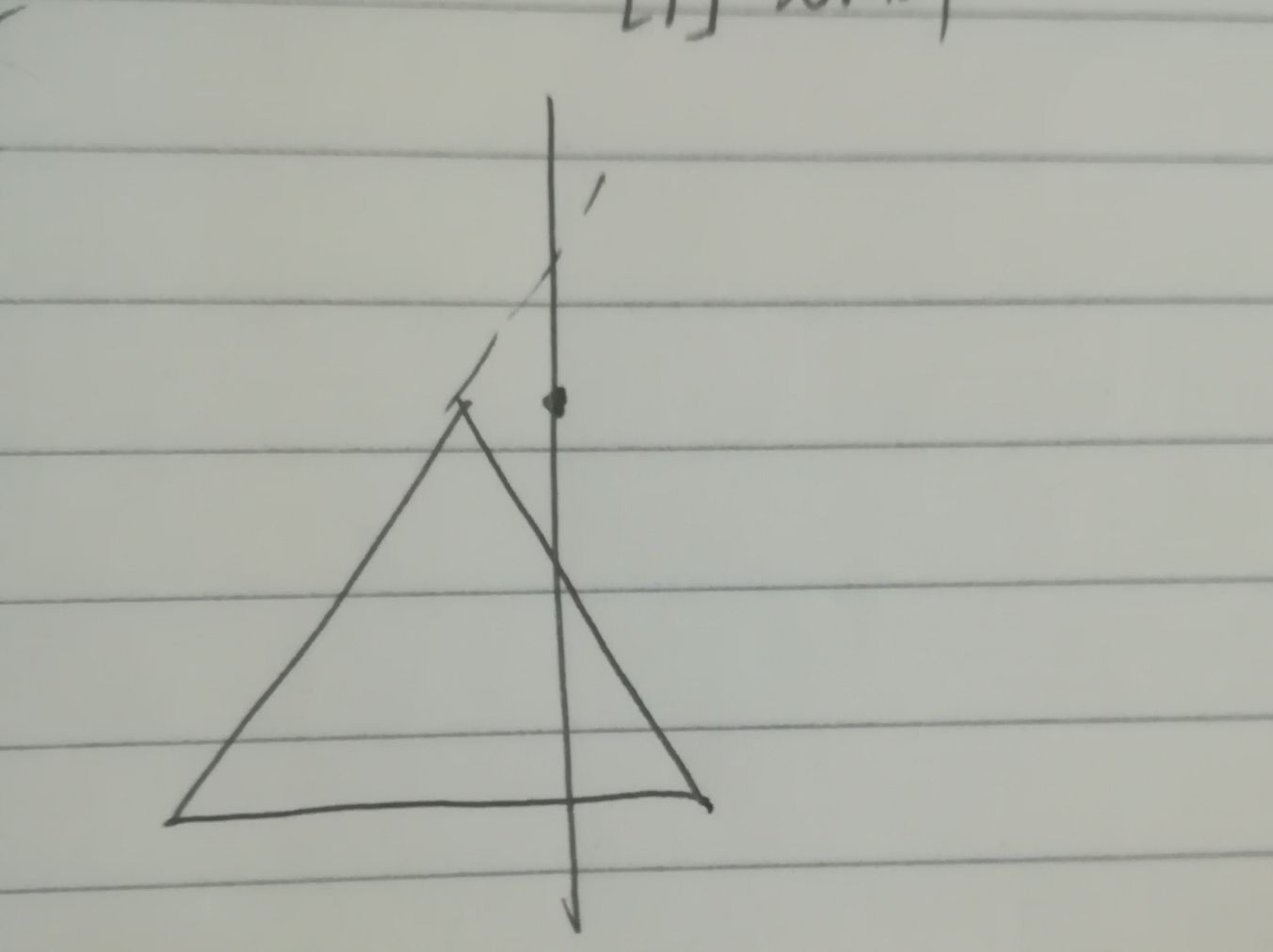
二是可能与底面相交，也不用特判，只需与前面的时间取较小值。

#include<bits/stdc++.h>
using namespace std;

double r, h, x, y, z, vx, vy, vz;

int main()
{
    int T, kase = ;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%lf%lf", &r, &h);
        scanf("%lf%lf%lf", &x, &y, &z);
        scanf("%lf%lf%lf", &vx, &vy, &vz);

        double a = h*h*vx*vx + h*h*vy*vy - r*r*vz*vz;
        double b = *h*h*x*vx + *h*h*y*vy - *r*r*z*vz + *r*r*h*vz;
        double c = h*h*x*x + h*h*y*y - h*h*r*r - r*r*z*z + *r*r*h*z;
        double detal = sqrt(b * b -  * a *c);
        double t1 = (-b + detal) / ( * a);
        //double x1 = x + vx * t1;
        double z1 = z + vz * t1;
        double t2 = (-b - detal) / ( * a);
        //double x2 = x + vx * t2;
        double z2 = z + vz * t2;

        //printf("a:%lf  b:%lf  c:%lf\n", a, b, c);
        //printf("detal:%lf  t1:%lf  t2:%lf\n", detal, t1, t2);

        //printf("Case %d: ", ++kase);
        double ans = 1e18;
        if(z1 >=  && z1 <= h && t1 > ) ans = min(ans, t1);  //²»ÄÜÓÃx,zÀ´ÅжÏ
        if(z2 >=  && z2 <= h && t2 > )  ans = min(ans, t2);
        double tmpt = -z / vz;
        double tmpx = x + vx * tmpt;
        double tmpy = y + vy *tmpt;
        if(fabs(vz)>1e-){
                if(tmpx >= -r && tmpx <= r && tmpy >= -r && tmpy <= r && tmpt > )  ans = min(ans, tmpt);
        }

        printf("Case %d: %.10lf\n", ++kase, ans);
    }
    return ;
}

参考链接：https://blog.csdn.net/du_mingm/article/details/89791220