OpenStack Cinder发展动态系列--Austin峰会

在Mitaka版本，Cinder团队在多个特性和领域取得了重大进展。

本文将做一个简要的介绍：关于在Mitaka版本已经完成的功能和特性，以及讨论在Newton版本将会开发的功能和特性。

1 Cinder Mitaka版本更新

1.1 复制：replication v2.0版本已废弃

实现了一套新的面向管理员的API replication v2.1，用来故障转移整个后端。

在cinder.conf配置文件的driver节点新增了卷类型。新增了复制的上报能力。

目前支持replication v2.1版本的厂商driver有：Dell，EMC，HPE，Huawei，IBM，Pure。SolidFire计划在N版本支持。

1.2 备份

当前版本备份特性已经支持全量和增量备份和不中断业务的备份。

在M版本新增了备份快照。

已经支持备份的driver有：Swift，Posix，NFS，GlusterFs，Ceph，IBM TSM。

在M版本新增了Google Cloud Storage的driver。

在M版本实现了backup服务与volume服务的解耦。

Backup服务部署不再强制需要跟volume服务部署在同一个节点。

1.3 双活HA

引入cinder volume服务的AA特性，带来了以下两个问题：本地文件锁，非原子状态事物。

解决方案是:增加分布式锁，移除API的竞争。

在N版本计划新增分布式job，新增资源清理处理，使用分布式锁替换manager的本地文件锁。

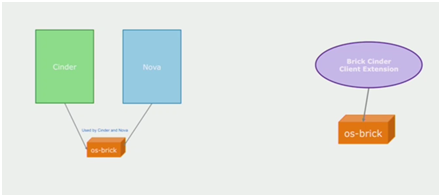
1.4 OS-Brick 和 Brick Cinder客户端扩展

os-brick包含cinder和nova用来挂载和解除挂载卷操作的初始化代码。

新增了brick cinder客户端扩展确保在没有Nova的情况下能够进行节点上的存储管理。

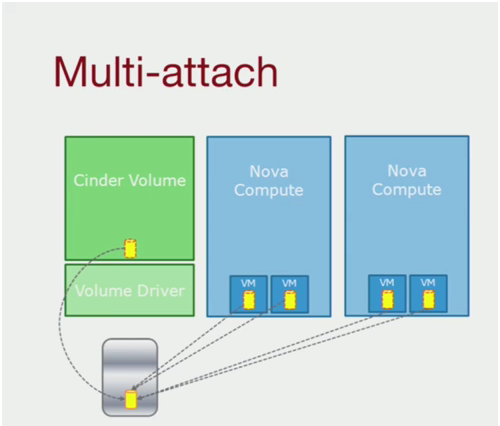
1.5 多重挂载

新增支持允许一个卷可以被挂载到多个主机或者vm上。

Cinder服务端和客户端都做了修改，Nova的修改也在M版本合入，但是目前还不可以使用所有的功能。

1.6 滚动升级

新增了RPC对象的兼容性，能够滚动升级依赖向后兼容性的RPC和version Object。

新增了在线schema的更新。

1.7 微版本

带来的新特性的开发变化。

已经实现了：新的/v3 endpoint；微版本服务代码；

新的微版本 3.1和3.2；Cinderclient支持 /v3 和微版本；

Devstack 支持/v3。有了微版本的支持，cinder Rest API在不影响旧有版本的API情况下就可以被改变。

通过在HTTP header中新增一个field versions并发送到client来实现。

1.8 驱动

新增的后端驱动有：Coho，DISCO，Fujitsu ETERNUS，Nexenta Edge and NexentaStor，Tegile。

2 Cinder Newton版本计划

2.1 复制

Replication特性下一步计划：新增一套面向租户的一套API（Tiramisu），实现分组的复制以及租户的测试灾难恢复的API。

2.2 备份

M版本已完成解除与volume服务的绑定，可以部署到多个物理节点上。

N版本计划开发：添加单元测试以及tempest测试用例，添加HA中的清理，修复单个backup服务性能问题等。

2.3 双活HA

为了支持cinder的双活特性新增了分布式锁，计划在N版本新增相关的压力测试。

2.4 微版本

N版本需要继续开发的有：

Tempest 测试用例修改。

功能性测试用例。

其他客户端适配cinder的 /v3 API。

编者注：本文来自OpenStack开源团队工程师陈莹