【2019.3.2】NOI 模拟赛

题目

题解（有些小错误）

H老爷的简短题解

请无视题目 $pdf$ 的第二行，信那句话的人都已经上清华了

听说大老爷切了 $250+$ 分，然后发现是两个人分着写三道题的，然后第一题还流假了…… $xswl$

---

T1

$10\%,\space n\le 16$

枚举

$20\%,\space K\le 10$

发现影响每个位置的决策只有前 $k$ 个，将每相邻 $k$ 个位置压缩成一个二进制状态，做 $DP$。

$20\%,\space Q=0$

分数规划？

强行钦定初始时全部选择正立表演，第 $i$ 个位置若有贡献则要付出 $A_i-B_i$ 的代价（说白了，一个位置如果要把正立表演换成倒立表演就有贡献，否则无贡献），那么每连续 $K$ 个节目中至少有 $P$ 个贡献。

列出 $N-K+1$ 个等式，第 $k$ 个等式为

$$(\sum_{k=i}^{k+K-1}C_k)-Y_i = P \space\space i∈[1,n-K+1],\space Y_i∈[0,K-P-Q]$$

其中 $C_i$ 表示第 $i$ 个位置是否贡献，$Y_i$ 表示 $[k,k+K-1]$ 这个节目段中那些无表演限制的节目中有多少个选择了贡献。

添加第 $0$ 个等式和第 $N-K+2$ 个等式，式子为 $0=0$。然后我们就可以差分了，把每相邻两个式子作差得到：

T2

$50\%,\space n\le 5000$

由于 $50$ 分做法比较显然，我就没考虑 $20$ 分的……给的题解说是枚举两种深度建虚树……

首先看到这种题会有一种直觉：$dis(a,b)=dis(a,c)=dis(b,c)$ 等价于 $dis(a,o)=dis(b,o)=dis(c,o)$，其中 $o$ 是树上一点。

也就是说，我们可以枚举树上一个中点，然后以这个点为根，找三个不同子树中的深度相同的点（即三个点到这个根的距离相等），这三个点就是组成一个合法的无序三元组。

这样会不会漏掉一些三元组？其实不会。

我们从好想的两个点入手证明：

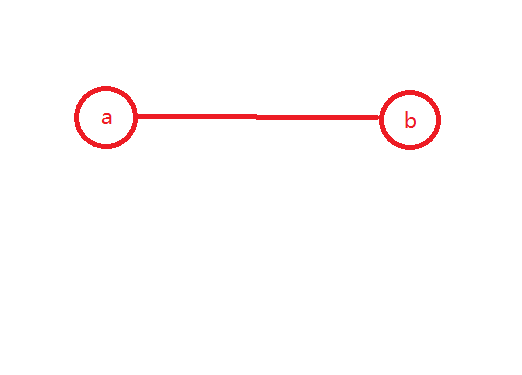
我们要添加一个点 $c$，使得 $dis(a,c)=dis(b,c)$。$dis(a,b)$ 不用考虑，如果 $dis(a,c)=dis(b,c)$ 这个条件能满足的话，让它们两个都等于 $dis(a,c)$ 就行了（$dis(a,c)$ 和 $dis(b,c)$ 达不到 $dis(a,b)$ 的情况可以被判掉，先不考虑）。

因为是在树上，所以 $a,b,c$ 三点只能有一条简单路径连接。

如果 $c$ 接在 $a$ 左边，$dis(b,c)$ 就必定大于 $dis(a,c)$，从而无法满足题目要求 $dis(a,b)=dis(a,c)=dis(b,c)$。

$c$ 接在 $b$ 右边同理。

所以 $c$ 只能从 $a,b$ 的简单路径上叉出去。

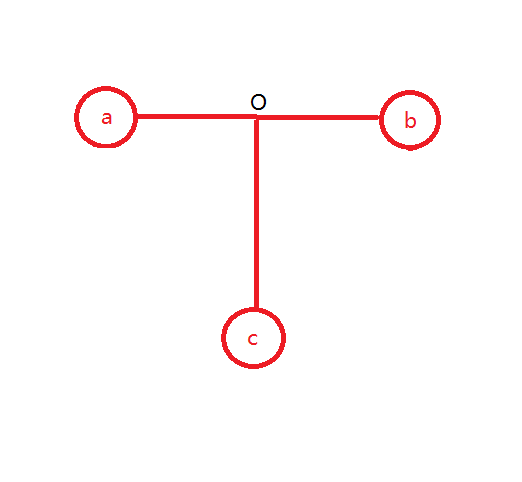
这时 $dis(a,b)=dis(a,c)=dis(b,c)$ 是有可能的。

设叉出的那个点为 $o$，因为 $dis(a,c)=dis(b,c)$，所以 $dis(a,c)-dis(o,c)=dis(b,c)-dis(o,c)$，$dis(a,o)=dis(b,o)$

同理推出 $dis(a,o)=dis(c,o)$

所以必定存在一个点 $o$ 满足 $dis(a,o)=dis(b,o)=dis(c,o)$， 我们只要枚举这个点 $o$ 即可。

对于枚举的一个点 $o$，设这个点为树根，满足 $dis(a,o)=dis(b,o)=dis(c,o)$ 的点 $a,b,c$ 一定分别在三棵不同子树中（否则在同一子树的两个点的简单路径不经过点 $o$，比如点 $a,c$ 在同一子树中，那这两点的最短路就不是 $dis(a,o)+dis(o,c)$，无法用以上证明来证明当前枚举点是这三点对应的中点 $o$）。

可以发现，同一深度的所有点的组合方案数可以直接列式计算（深度就是一个点到树根 $o$ 的距离）。

由于一开始我理解错题意了，写成了求所有有序三元组的贡献和……不过根据三个数有 $6$ 种排列的性质，可知答案除以 $6$ 就是所有无序三元组的贡献和……所以我直接说有序三元组的贡献和的求法了。

考虑枚举一个深度的一个点（其实就 $dfs$ 搜一下就可以了）。对于这个点，它可以跟其它所有子树的所有同深度的点组成三元组，我们把这个点固定在三元组的第一位，后两位就一定是其它子树中同深度的点了。以后找那些同深度的点时，就会把这个点放在三元组的第二位、第三位，再算一遍贡献相同、顺序不同的三元组。由于每个点都会因此被固定在三个位置各一次，所以可以证明这样一定能算全所有方案。

但是我们显然不可能再用一个或两个循环枚举其它子树中同深度的点，因为现在的复杂度已经是 $O(n^2)$ 了。

我们回头观察一下一个三元组的贡献：$V_a\times V_b + V_a\times V_c + V_b\times V_c$

其实到这里已经可以做了，因为三项是相加，可以拆开算，每项都可以结合预处理做到 $O(1)$ 计算，把三个总和加起来就是固定当前点在第一位时，所有三元组的贡献和了。

题外话：

但我为了少算点东西，取了个巧……

既然同一个三元组会以不同顺序计算 $6$ 次，我们可以换位思考，将一个三元组的贡献改为 $3\times (V_b\times V_c)$，这样这个三元组被以不同顺序计算 $6$ 次后，贡献的总和与原来相同？

这样就只需要算 $V_b\times V_c$，不用预处理其它子树中同深度的所有点的权值和了。

code（取模写得丑见谅哈）

 #include<bits/stdc++.h>
 #define rep(i,x,y) for(int i=(x);i<=(y);++i)
 #define dwn(i,x,y) for(int i=(x);i>=(y);--i)
 #define rep_e(i,u) for(int i=hd[u];i;i=e[i].nxt)
 #define ll long long
 #define int long long
 #define N 5005
 #define mod 998244353
 #define inv_6 166374059
 using namespace std;
 inline int read(){
     int x=; bool f=; char c=getchar();
     for(;!isdigit(c);c=getchar()) if(c=='-') f=;
     for(; isdigit(c);c=getchar()) x=(x<<)+(x<<)+(c^'');
     if(f) return x;
     return -x;
 }
 int n,V[N];
 struct edge{int v,nxt;}e[N<<];
 int hd[N],cnt;
 inline void add(int u,int v){e[++cnt]=(edge){v,hd[u]}, hd[u]=cnt;}
 int c[N][N],c_sum[N],self_pf[N],son_num,cnt_three[N];
 bool vis[N],three[N][N];
 void dfs(int u,int fa,int dis){
     (c[son_num][dis]+=V[u])%=mod, (c_sum[dis]+=V[u])%=mod;
     if(!three[son_num][dis]) three[son_num][dis]=, ++cnt_three[dis];
     //printf("dfs:%d %d %d\n",u,dis,V[u]);
     rep_e(i,u) if(e[i].v!=fa) dfs(e[i].v,u,dis+);
 }
 int mxDis;
 void getPf(int u,int fa,int dis){
     if(!vis[dis]) (self_pf[dis]+=c[son_num][dis]*c[son_num][dis]%mod)%=mod, vis[dis]=, mxDis=max(mxDis,dis);
     rep_e(i,u) if(e[i].v!=fa) getPf(e[i].v,u,dis+);
 }
 int ans;
 void getAns(int u,int fa,int dis){
     if(cnt_three[dis]>=){
         int k=(c_sum[dis]*c_sum[dis]%mod-self_pf[dis]-c[son_num][dis]*(c_sum[dis]-c[son_num][dis])*%mod+mod)%mod;
         //printf("%d : %d %d %d %d %d\n",u,dis,c_sum[dis]*c_sum[dis],self_pf[dis]*2,c[son_num][dis],c[son_num][dis]*(c_sum[dis]-c[son_num][dis])*2);
         //cout<<k<<endl;
         (ans+=k*%mod)%=mod;
     }
     rep_e(i,u) if(e[i].v!=fa) getAns(e[i].v,u,dis+);
 }
 void clear(int u,int fa,int dis){
     c[son_num][dis]=c_sum[dis]=cnt_three[dis]=self_pf[dis]=, three[son_num][dis]=;
     rep_e(i,u) if(e[i].v!=fa) clear(e[i].v,u,dis+);
 }
 signed main(){
     freopen("tree.in","r",stdin);
     freopen("tree.out","w",stdout);
     n=read();
     int u,v;
     rep(i,,n) u=read(), v=read(), add(u,v), add(v,u);
     rep(i,,n) V[i]=read();
     rep(i,,n){
         //printf("start:%d\n",i);
         son_num=;
         rep_e(j,i) ++son_num, dfs(e[j].v,i,);
         son_num=;
         rep_e(j,i) ++son_num, mxDis=, getPf(e[j].v,i,), fill(vis+,vis+mxDis+,);
         son_num=;
         rep_e(j,i) ++son_num, getAns(e[j].v,i,);
         son_num=;
         rep_e(j,i) ++son_num, clear(e[j].v,i,);
     }
     cout<<ans*inv_6%mod<<endl;
     return ;
 }

$50\%,\space n\le 5000$

群众：蛤，怎么还是 $50$ 分？

别着急，这里用的是推 $dp$ 方程的方法，可以引出正解（我写的 $50$ 分就是小学生做法没什么拓展性）

$100\%$

前置知识：长链剖分