【2018.12.17】NOI模拟赛4

题目

WZJ题解

T1

T2

T3

后缀自动机+（$parents$ 树）树链剖分

发现有大量子串需要考虑，考虑摁死子串的一端。

首先，这题显然是一道离线题，因为所有的询问都是 $1$ 到 某个数，也就是一个前缀和，完全可以递推处理。

所以先把所有的询问按 $m$ 从小到大排序。

然后我们画画 $KMP$ 树，发现一些神奇的性质。

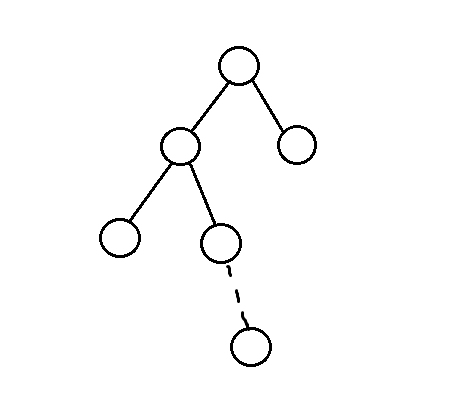
设虚边下面那个点为新加入的一个点（字符），如果这个点的编号（编号 即插入的这个字符是原串的第几位） 比这棵树上面原有的那些点的编号都大的话，那它一定会成为叶子节点。

也就是说，如果你按顺序依次插入原串的每一位字符，每个新加入的字符一定都会加到树的叶子处。

这样的话，上面那些以前插入的节点的深度都没有变，新加入一个点不会对之前的任何点的贡献造成影响。

所以所有右端点范围在 $[1,i]$ 内的子串的答案 就是所有右端点范围在 $[1,i-1]$ 内的子串的答案 $+$ 所有右端点在第 $i$ 位的子串的答案。

这个可以二维前缀和递推求，即开一个 $fakeans$ 动态累加 所有右端点范围在 $[1,i]$ 内的子串的答案，再开一个 $ans$ 动态累加累加 $fakeans$，这样就算上了每一位固定为右端点 且左端点任意时的所有子串，即所有左右端点情况的子串。

我们考虑加入第 $i$ 位字符时，这个字符对答案的贡献怎么算。

由于加入的这个字符一定在树的最底下（叶子），所以它的深度就是 树

如图，也就是以原串第 $i$ 位为结尾的 $i$ 个后缀串。