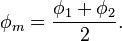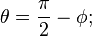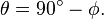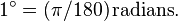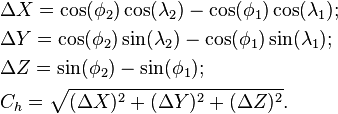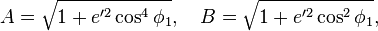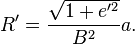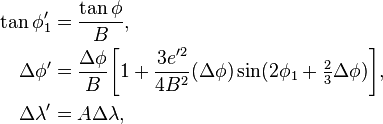Geographical distance

Introduction

Calculating the distance between geographical coordinates is based on some level of abstraction; it does not provide an exact distance, which is unattainable if one attempted to account for every irregularity in the surface of the earth.^[1] Common abstractions for the surface between two geographic points are:

Flat surface;
Spherical surface;
Ellipsoidal surface.

All abstractions above ignore changes in elevation. Calculation of distances which account for changes in elevation relative to the idealized surface are not discussed in this article.

Nomenclature

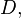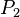Distance, is calculated between two points, and . The geographical coordinates of the two points, as (latitude, longitude) pairs, are 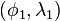and 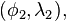respectively. Which of the two points is designated as is not important for the calculation of distance.

Latitude and longitude coordinates on maps are usually expressed in degrees. In the given forms of the formulae below, one or more values must be expressed in the specified units to obtain the correct result. Where geographic coordinates are used as the argument of a trigonometric function, the values may be expressed in any angular units compatible with the method used to determine the value of the trigonometric function. Many electronic calculators allow calculations of trigonometric functions in either degrees or radians. The calculator mode must be compatible with the units used for geometric coordinates.

Differences in latitude and longitude are labeled and calculated as follows:

It is not important whether the result is positive or negative when used in the formulae below.

"Mean latitude" is labeled and calculated as follows:

Colatitude is labeled and calculated as follows:

For latitudes expressed in radians:

For latitudes expressed in degrees:

Unless specified otherwise, the radius of the earth for the calculations below is:

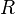= 6,371.009 kilometers = 3,958.761 statute miles = 3,440.069 nautical miles.

= Distance between the two points, as measured along the surface of the earth and in the same units as the value used for radius unless specified otherwise.

Singularities and discontinuity of latitude/longitude

Longitude has singularities at the Poles (longitude is undefined) and a discontinuity at the ±180° meridian. Also, planar projections of the circles of constant latitude are highly curved near the Poles. Hence, the above equations for delta latitude/longitude (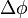, 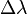) and mean latitude () may not give the expected answer for positions near the Poles or the ±180° meridian. Consider e.g. the value of 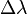(“east displacement”) when 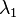and 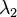are on either side of the ±180° meridian, or the value of (“mean latitude”) for the two positions (=89°, 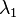=45°) and (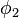=89°, 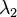=−135°).

If a calculation based on latitude/longitude should be valid for all Earth positions, it should be verified that the discontinuity and the Poles are handled correctly. Another solution is to use n-vector instead of latitude/longitude, since this representation does not have discontinuities or singularities.

Flat-surface formulae

A planar approximation for the surface of the earth may be useful over small distances. The accuracy of distance calculations using this approximation become increasingly inaccurate as:

The separation between the points becomes greater;
A point becomes closer to a geographic pole.

The shortest distance between two points in plane is a straight line. The Pythagorean theorem is used to calculate the distance between points in a plane.

Even over short distances, the accuracy of geographic distance calculations which assume a flat Earth depend on the method by which the latitude and longitude coordinates have been projected onto the plane. The projection of latitude and longitude coordinates onto a plane is the realm of cartography.

The formulae presented in this section provide varying degrees of accuracy.

Spherical Earth projected to a plane

This formula takes into account the variation in distance between meridians with latitude:

where:

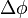and

are in radians;

must be in units compatible with the method used for determining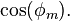

To convert latitude or longitude to radians use

Note: This approximation is very fast and produces fairly accurate result for small distances^{[citation needed]}. Also, when ordering locations by distance, such as in a database query, it is much faster to order by squared distance, eliminating the need for computing the square root.

Ellipsoidal Earth projected to a plane

The FCC prescribes essentially the following formulae in 47 CFR 73.208 for distances not exceeding 475 km /295 miles:^[2]

where

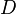= Distance in kilometers;

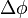and

are in degrees;

must be in units compatible with the method used for determining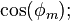

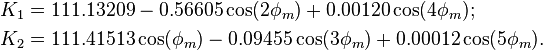
It may be interesting to note that:

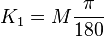= kilometers per degree of latitude difference;

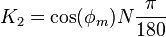= kilometers per degree of longitude difference;

where

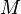and

are the meridional and its perpendicular, or "normal", radii of curvature (the expressions in the FCC formula are derived from the binomial series expansion form of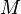

and

, set to the Clarke 1866 reference ellipsoid).

Polar coordinate flat-Earth formula

where the colatitude values are in radians. For a latitude measured in degrees, the colatitude in radians may be calculated as follows:

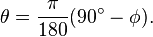
Spherical-surface formulae

Main article: Great-circle distance

If we are willing to accept a possible error of 0.5%, we can use formulas of spherical trigonometry on the sphere that best approximates the surface of the earth.

The shortest distance along the surface of a sphere between two points on the surface is along the great-circle which contains the two points.

The great-circle distance article gives the formula for calculating the distance along a great-circle on a sphere about the size of the Earth. That article includes an example of the calculation.

Tunnel distance

A tunnel between points on Earth is defined by a line through three-dimensional space between the points of interest. The great circle chord length may be calculated as follows for the corresponding unit sphere:

The tunnel distance between points on the surface of a spherical Earth is 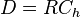. For short distances (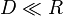), this underestimates the great circle distance by .

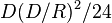Ellipsoidal-surface formulae

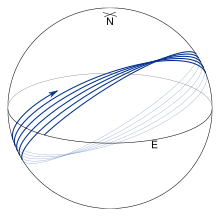
Main article: Geodesics on an ellipsoid

Geodesic on an oblate ellipsoid

An ellipsoid approximates the surface of the earth much better than a sphere or a flat surface does. The shortest distance along the surface of an ellipsoid between two points on the surface is along the geodesic. Geodesics follow more complicated paths than great circles and in particular, they usually don't return to their starting positions after one circuit of the earth. This is illustrated in the figure on the right where f is taken to be 1/50 to accentuate the effect. Finding the geodesic between two points on the earth, the so-called inverse geodetic problem, was the focus of many mathematicians and geodesists over the course of the 18th and 19th centuries with major contributions by Clairaut,^[3] Legendre,^[4] Bessel,^[5] and Helmert.^[6] Rapp^[7] provides a good summary of this work.

Methods for computing the geodesic distance are widely available in geographical information systems, software libraries, standalone utilities, and online tools. The most widely used algorithm is by Vincenty,^[8] who uses a series which is accurate to third order in the flattening of the ellipsoid, i.e., about 0.5 mm; however, the algorithm fails to converge for points that are nearly anti-podal. (For details, see Vincenty's formulae.) This defect is cured in the algorithm given by Karney,^[9] who employs series which are accurate to sixth order in the flattening. This results in an algorithm which is accurate to full double precision and which converges for arbitrary pairs of points on the earth. This algorithm is implemented in GeographicLib.^[10]

The exact methods above are feasible when carrying out calculations on a computer. They are intended to give millimeter accuracy on lines of any length; we can use simpler formulas if we don't need millimeter accuracy, or if we do need millimeter accuracy but the line is short. Rapp,^[11] Chap. 6, describes the Puissant method, the Gauss mid-latitude method, and the Bowring method.^[12]

Lambert's formula for long lines

Lambert's formulae^[13] give accuracy on the order of 10 meters over thousands of kilometers. First convert the latitudes , of the two points to reduced latitudes ,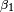

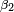
where is the flattening. Then calculate the central angle in radians between two points 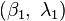and on a sphere in the usual way (law of cosines or haversine formula), with longitudes 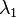and being the same on the sphere as on the spheroid.

where is the equatorial radius of the chosen spheroid.

On the GRS 80 spheroid Lambert's formula is off by

0 North 0 West to 40 North 120 West, 12.6 meters

0N 0W to 40N 60W, 6.6 meters

40N 0W to 40N 60W, 0.85 meter

Bowring's method for short lines

Bowring maps the points to a sphere of radius R′, with latitude and longitude represented as φ′ and λ′. Define

where the second eccentricity squared is

The spherical radius is

(The Gaussian curvature of the ellipsoid at φ₁ is 1/R′².) The spherical coordinates are given by

where , , , 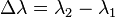. The resulting problem on the sphere may be solved using the techniques for great-circle navigation to give approximations for the spheroidal distance and bearing. Detailed formulas are given by Rapp,^[11] §6.5 and Bowring.^[12]

References

http://www.cartography.org.uk/default.asp?contentID=749
http://edocket.access.gpo.gov/cfr_2005/octqtr/pdf/47cfr73.208.pdf
Clairaut, A. C. (1735). "Détermination géometrique de la perpendiculaire à la méridienne tracée par M. Cassini" [Geometrical determination of the perpendicular to the meridian drawn by Jacques Cassini]. Mémoires de l'Académie Royale des Sciences de Paris 1733 (in French): 406–416.
Legendre, A. M. (1806). "Analyse des triangles tracées sur la surface d'un sphéroïde" [Analysis of spheroidal triangles]. Mémoires de l'Institut National de France (in French) (1st semester): 130–161.
Bessel, F. W. (2010) [1825]. . Translated by C. F. F. Karney & R. E. Deakin. "The calculation of longitude and latitude from geodesic measurements". Astronomische Nachrichten 331 (8): 852–861. arXiv:0908.1824. doi:10.1002/asna.201011352. English translation of Astron. Nachr. 4, 241–254 (1825). Errata.
Helmert, F. R. (1964) [1880]. Mathematical and Physical Theories of Higher Geodesy 1. St. Louis: Aeronautical Chart and Information Center. English translation of Die Mathematischen und Physikalischen Theorieen der Höheren Geodäsie, Vol. 1 (Teubner, Leipzig, 1880).
Rapp, R. H. (March 1993). Geometric Geodesy, Part II (Technical report). Ohio State University. Retrieved 2011-08-01.
Vincenty, T. (April 1975). "Direct and Inverse Solutions of Geodesics on the Ellipsoid with application of nested equations" (PDF). Survey Review 23 (176): 88–93. doi:10.1179/sre.1975.23.176.88. Retrieved 2009-07-11. Addendum: Survey Review 23 (180): 294 (1976).
Karney, C. F. F. (2013). "Algorithms for geodesics". Journal of Geodesy 87 (1): 43–42. arXiv:1109.4448. Bibcode:2013JGeod..87...43K. doi:10.1007/s00190-012-0578-z (open access). Addenda.
Karney, C. F. F. (2013). "GeographicLib". 1.32.
Rapp, R, H, (1991). Geometric Geodesy, Part I (Report). Ohio Start Univ.
Bowring, B. R. (1981). "The direct and inverse problems for short geodesics lines on the ellipsoid". Surveying and Mapping 41 (2): 135–141.

Lambert, W. D (1942). "The distance between two widely separated points on the surface of the earth". J. Washington Academy of Sciences 32 (5): 125–130.

External links

Ivis, Frank (2006). "Calculating Geographic Distance: Concepts and Methods" (PDF).
An online geodesic calculator (based on GeographicLib).
An online geodesic bibliography.
Tripstance tool - Online distance calculator.
Online Distance Calculator Tool - road distance calculator.

Categories: