HDU 1025 Constructing Roads In JGShining's Kingdom[动态规划/nlogn求最长非递减子序列]

Constructing Roads In JGShining's Kingdom

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 27358    Accepted Submission(s): 7782

Problem Description

JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.

Half
of these cities are rich in resource (we call them rich cities) while
the others are short of resource (we call them poor cities). Each poor
city is short of exactly one kind of resource and also each rich city is
rich in exactly one kind of resource. You may assume no two poor cities
are short of one same kind of resource and no two rich cities are rich
in one same kind of resource.

With the development of industry,
poor cities wanna import resource from rich ones. The roads existed are
so small that they're unable to ensure the heavy trucks, so new roads
should be built. The poor cities strongly BS each other, so are the rich
ones. Poor cities don't wanna build a road with other poor ones, and
rich ones also can't abide sharing an end of road with other rich ones.
Because of economic benefit, any rich city will be willing to export
resource to any poor one.

Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.

The
location of Rich City 1 is on the left of all other cities, Rich City 2
is on the left of all other cities excluding Rich City 1, Rich City 3
is on the right of Rich City 1 and Rich City 2 but on the left of all
other cities ... And so as the poor ones.

But as you know, two
crossed roads may cause a lot of traffic accident so JGShining has
established a law to forbid constructing crossed roads.

For example, the roads in Figure I are forbidden.

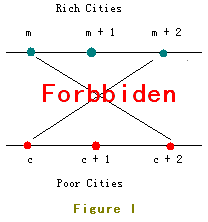
In
order to build as many roads as possible, the young and handsome king
of the kingdom - JGShining needs your help, please help him. ^_^

 

Input

Each
test case will begin with a line containing an integer n(1 ≤ n ≤
500,000). Then n lines follow. Each line contains two integers p and r
which represents that Poor City p needs to import resources from Rich
City r. Process to the end of file.

 

Output

For each test case, output the result in the form of sample.
You should tell JGShining what's the maximal number of road(s) can be built.

 

Sample Input

2
1 2
2 1
3
1 2
2 3
3 1

 

Sample Output

Case 1:
My king, at most 1 road can be built.

Case 2:
My king, at most 2 roads can be built.

Hint

Huge input, scanf is recommended.

 

Author

JGShining（极光炫影）

 

Recommend

We have carefully selected several similar problems for you:  1081 1074 1078 1080 1114

[题意]:有n个富饶的城市和n个贫穷的城市，然后每个富饶的城市有一种多余的资源，没有两个城市多余的资源一样， 每个贫穷的城市缺少一种资源，没有两个城市缺少的资源一样，要在他们之间建路，中间不能相交，问最多建几条路 ，当两个城市缺少的和多余的刚好匹配时，就表示能建路，但是建不建不一定

 

---

[分析]:

假设存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7，可以看出来它的LIS长度为5。
下面一步一步试着找出它。
我们定义一个序列B，然后令 i = 1 to 9 逐个考察这个序列。
此外，我们用一个变量Len来记录现在最长算到多少了
首先，把d[1]有序地放到B里，令B[1] = 2，就是说当只有1一个数字2的时候，长度为1的LIS的最小末尾是2。这时Len=1
然后，把d[2]有序地放到B里，令B[1] = 1，就是说长度为1的LIS的最小末尾是1，d[1]=2已经没用了,这时Len=1
接着，d[3] = 5，d[3]>B[1]，所以令B[1+1]=B[2]=d[3]=5，就是说长度为2的LIS的最小末尾是5，这时候B[1..2] = 1, 5，Len＝2
再来，d[4] = 3，它正好加在1,5之间,放在1的位置显然不合适,因为1小于3,长度为1的LIS最小末尾应该是1,长度为2的LIS最小末尾是3，

于是可以把5淘汰掉，这时候B[1..2] = 1, 3，Len = 2
继续，d[5] = 6，它在3后面，因为B[2] = 3, 而6在3后面，于是很容易可以推知B[3] = 6, 这时B[1..3] = 1, 3, 6，还是很容易理解吧？ Len = 3.
第6个, d[6] = 4，你看它在3和6之间，于是我们就可以把6替换掉，得到B[3] = 4。B[1..3] = 1, 3, 4,Len继续等于3
第7个, d[7] = 8，它很大，比4大，于是B[4] = 8。Len变成4了
第8个, d[8] = 9，得到B[5] = 9，Len继续增大，到5了。
最后一个, d[9] = 7，它在B[3] = 4和B[4] = 8之间，So最新的B[4] =7，B[1..5] = 1, 3, 4, 7, 9，Len = 5。
于是我们知道了LIS的长度为5。
注意。这个1,3,4,7,9不是LIS，它只是存储的对应长度LIS的最小末尾。有了这个末尾，我们就可以一个一个地插入数据。

虽然最后一个d[9] = 7更新进去对于这组数据没有什么意义，但是如果后面再出现两个数字8和9.那么就可以把8更新到d[5],
9更新到d[6]，得出LIS的长度为6。
然后应该发现一件事情了:在B中插入数据是有序的，而且是进行替换而不需要挪动—也就是说，我们可以使用二分查找，

将每一个数字的插入时间优化到O(logN)

---

 

 

[代码]:

/*
输入一个m，n分别表示成m组,一共有n个数
即将n个数分成m组，
m组的和加起来得到最大值并输出。
*/
#include <bits/stdc++.h>
using namespace std;
const int N=;
#define INF 0x7fffffff

int n;
int a[N],dp[N];

int main()
{
    int t=;
    while(cin>>n)
    {
        int x,y;
        for(int i=;i<=n;i++)
        {
            scanf("%d%d",&x,&y);
            a[x]=y;
        }
        for(int i=;i<=n;i++) dp[i]=INF;
        int ans=;
        for(int i=;i<=n;i++)
        {
            int tmp=lower_bound(dp+,dp+n+,a[i])-dp;
            dp[tmp]=a[i];
            ans=max(ans,tmp);
        }
        printf("Case %d:\nMy king, at most %d road%s can be built.\n\n",++t,ans,ans==?"":"s");
    }
}

/*
假设要寻找最长上升子序列的序列是a[n]，然后寻找到的递增子序列放入到数组dp中。

（1）当遍历到数组a的第一个元素的时候，就将这个元素放入到dp数组中，以后遍历到的元素都和已经放入到dp数组中的元素进行比较；

（2）如果比dp数组中的每个元素都大，则将该元素插入到dp数组的最后一个元素，并且dp数组的长度要加1；

（3）如果比dp数组中最后一个元素小，就要运用二分法进行查找，查找出第一个比该元素大的最小的元素，然后将其替换。

在这个过程中，只重复执行这两步就可以了，最后b数组的长度就是最长的上升子序列长度。例如：如该数列为：

5 9 4 1 3 7 6 7

那么：

5 //加入
5 9 //加入
4 9 //用4代替了5
1 9 //用1代替4
1 3 //用3代替9
1 3 7 //加入
1 3 6 //用6代替7
1 3 6 7 //加入

最后b中元素的个数就是最长递增子序列的大小，即4。

要注意的是最后数组里的元素并不就一定是所求的序列，

例如如果输入 2 5 1

那么最后得到的数组应该是 1 5

而实际上要求的序列是 2 5
*/

#include <bits/stdc++.h>
using namespace std;
const int N=;
#define INF 0x7fffffff

int n;
int a[N],dp[N];
int Find(int num,int l,int r)//用二分查找的方法找到一个位置，使得num>dp[i-1] 并且num<dp[i],并用num代替dp[i]
{
    int mid;
    while(l<=r)
    {
        mid=(l+r)>>;
        if(num>=dp[mid])
            l=mid+;
        else
            r=mid-;
    }
    return l;
}
int DP(int n)
{
    int len,pos;
    dp[]=a[];
    len=;
    for(int i=;i<=n;i++)
    {
        if(a[i]>dp[len])//如果a[i]比dp[]数组中最大还大直接插入到后面即可
        {
            len++;
            dp[len]=a[i];
        }
        else//用二分的方法在b[]数组中找出第一个比a[i]大的位置并且让a[i]替代这个位置
        {
            pos=Find(a[i],,len);
            dp[pos]=a[i];
        }
    }
    return len;
}
int main()
{
    int t=;
    while(cin>>n)
    {
        int x,y;
        for(int i=;i<=n;i++)
        {
            scanf("%d%d",&x,&y);
            a[x]=y;
        }
        int ans=DP(n);
        printf("Case %d:\nMy king, at most %d road%s can be built.\n\n",++t,ans,ans==?"":"s");
    }
}

注释详解