Odoo超售订单
当
交付给客户的货物多于订购的数量时,就形成'超售'状态; 对于超售的部分,需要进行开票处理,以及根据情况修改交货
发生超售的前提是,产品开票策略为 '按订购数量开票'
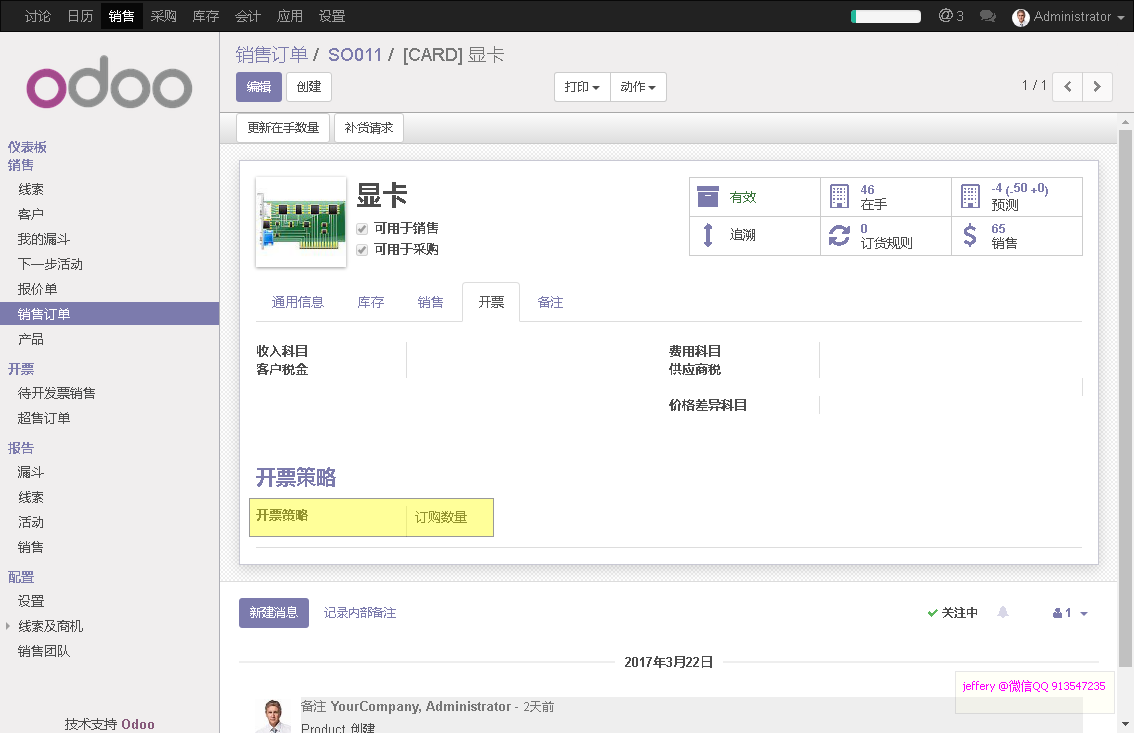
同时需要
允许修改
订单

超售可能是以下情形下发生的
- 订单确认、开立发票之后,修改订单数量,导致 订单金额和已开立的发票之间存在差异,以及交货数量发生变化
- 订单确认、开立发票之后,修改订单价格,导致 订单金额和已开立的发票之间存在差异
- 订单确认、开立发票之后,修改订单数量,导致
订单金额和已开立的发票之间存在差异,以及交货数量发生变化
此时,在
订单再次建立发票,
系统将会建立退款发票,
例如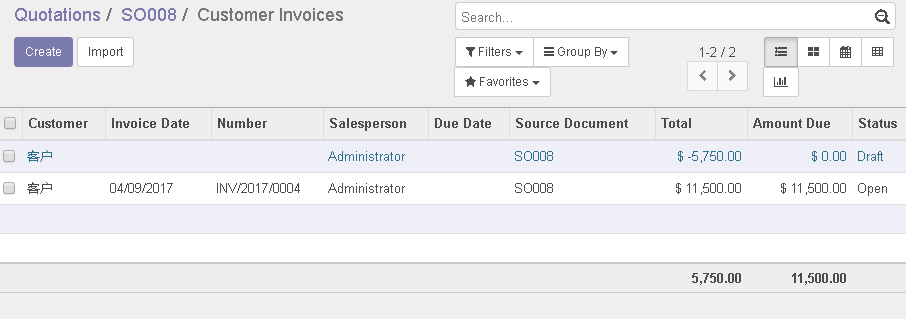
因为
交货是基于之前的
订单建立,因此,需要
取消它,
然后基于它
复制一份,
并修改
交货数量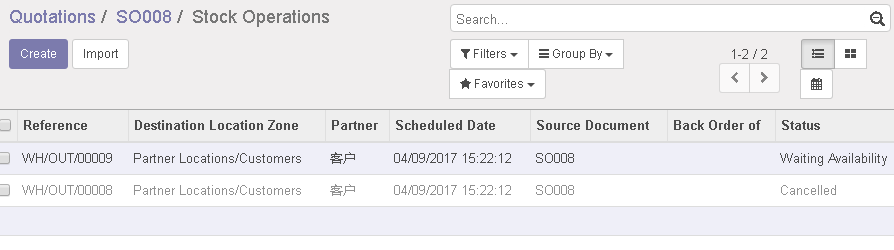
订单修改完成后,将订单设置为 'lock'
- 在订单确认、开立发票之后,修改订单价格,导致
订单金额和已开立的发票之间存在差异,以及交货数量发生变化
此时,
修改
原始订购数量为
零,
并增加
新的订单行,数量为
原始订购数量,但是
单价修改为
新单价,
如下

再次
建立
发票,
系统将计算出
退款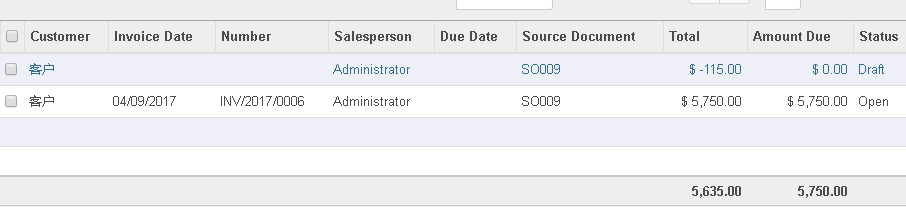
此时需要
验证
交货单是否正确,
发现
增加的订单行将会
增加发货数量
因此,需要 取消它, 然后基于它 复制一份, 并修改 交货数量

订单修改完成后,将订单设置为 'lock'
Odoo超售订单的更多相关文章
- Odoo销售模块
转载请注明原文地址:https://www.cnblogs.com/ygj0930/p/10825988.html 一:销售模块 销售模块的用途: 1)管理销售团队.销售人员:维护销售产品: 2)管理 ...
- 全网首发! Odoo 订单分解执行及供应链管理免费开源解决方案
引言 前一篇介绍了佛山王朝家具的案例背景.佛山王朝家具公司在全国有30多家门店,三个生产工厂.王朝家具有六大痛点问题: 订单迫切需要实现电子化管理及在线签名 总部分单工作量大,供应链效率低 配送和售后 ...
- Odoo中最小库存规则和按订单生成规则的区别
---恢复内容开始--- 最小库存规则(Minimum stock rule)用来保证你的库存产品数量总是不会低于设定的最小库存数量.用来保证产品生产和回到客户的需求.当库存产品低于这个最小库存数量时 ...
- odoo之带出历史订单产品
这是在sale_origin中下由两张单子{sale_origin_line和history_order} class history_order(osv.osv): _name="hist ...
- odoo订餐系统之订单相关知识点理解
1.对重载函数name_get的理解 第一,此函数位于Model基类中,返回值是一个list列表,列表中的每个值是如(key,value)形式的键值对,此处为(id,name). 第二,在自己的Mod ...
- odoo订餐系统之订单设计
订餐系统的主要功能便是用户下单部分,这里我们分为表头mylunch_order和表体mylunch_order_line两张主要的数据表,表头主要记录订单的一些通用信息,比如下单的操作人员 下单日期 ...
- odoo开发历史订单需求整体思路
第一步:找到客户对应页面,并找到他所下过的销售订单,用数据库语句查出所有数据,并去除重复数据,显示在前端, sql="select DISTINCT t2.product_id as pro ...
- odoo 订单打印 会出现字体. ........... 虚线问题
在表头加 红色部分 <?xml version="1.0" encoding="utf-8"?><openerp> <data&g ...
- Odoo 二次开发教程(四)-只读、唯一性验证和ORM方法介绍
一.只读和唯一性验证 只读的设置有两种方法,一种是实在字段定义时设置为只读,第二种是在页面视图中进行设置. 接前例,我们将学生(tech.student)的名字name字段设置成只读. 方法一:字段定 ...
随机推荐
- Python-函数参数的传递
作者:Vamei 出处:http://www.cnblogs.com/vamei,感谢博主的分享, python的函数参数传递有这样的几种形式: 1.位置传递 2.关键字传递 3.参数默认值传递 4. ...
- Leetcode 481.神奇字符串
神奇字符串 神奇的字符串 S 只包含 '1' 和 '2',并遵守以下规则: 字符串 S 是神奇的,因为串联字符 '1' 和 '2' 的连续出现次数会生成字符串 S 本身. 字符串 S 的前几个元素如下 ...
- [adb 学习篇] adb pull
adb pull E:\uitest\testcase\CaseDemo\testcase\3dmark\3DMarkAndroid /sdcard/3DMarkAndroid 假设: E: ...
- Difference between git remote add and git clone
http://stackoverflow.com/questions/4855561/difference-between-git-remote-add-and-git-clone git remot ...
- 学习 WebService 第五步:在Local创建测试用WebService(WSDL)
[准备] Eclipse+Tomcat7(Tomcat端口修改为不冲突的值) axis2 1.7.7 jar包(没有来这里下载:http://www.apache.org/dyn/closer.lua ...
- [USACO07NOV]牛继电器Cow Relays (最短路,DP)
题目链接 Solution 非正解 似乎比较蛇啊,先个一个部分分做法,最短路+\(DP\). 在求最短路的堆或者队列中存储元素 \(dis_{i,j}\) 代表 \(i\) 这个节点,走了 \(j\) ...
- 【python接口自动化】httpUtils
# coding=utf8 import requests from common.logger import Logger import logging class httpUtils: logge ...
- 我要好offer之 系统基础大总结
1. APUE Unix环境高级编程 (1) Unix基础知识: 内核->系统调用->shell和库函数->应用软件 (2) 文件I/O:read函数返回值.进程的文件描述符表.文件 ...
- 我要好offer之 排序算法大总结
1. 插入排序 (1) 直接插入排序 void StraightInsertionSort(std::vector<int>& num) { || num.size() == ) ...
- LeetCode OJ——Minimum Depth of Binary Tree
http://oj.leetcode.com/problems/minimum-depth-of-binary-tree/ 贡献了一次runtime error,因为如果输入为{}即空的时候,出现了c ...
