【构造题贪心】cf1041E. Tree Reconstruction

比赛时候还是太慢了……要是能做快点就能上分了

Monocarp has drawn a tree (an undirected connected acyclic graph) and then has given each vertex an index. All indices are distinct numbers from 11 to nn. For every edge ee of this tree, Monocarp has written two numbers: the maximum indices of the vertices of the two components formed if the edge ee (and only this edge) is erased from the tree.

Monocarp has given you a list of n−1n−1 pairs of numbers. He wants you to provide an example of a tree that will produce the said list if this tree exists. If such tree does not exist, say so.

Input

The first line contains one integer nn (2≤n≤10002≤n≤1000) — the number of vertices in the tree.

Each of the next n−1n−1 lines contains two integers aiai and bibi each (1≤ai<bi≤n1≤ai<bi≤n) — the maximal indices of vertices in the components formed if the ii-th edge is removed.

Output

If there is no such tree that can produce the given list of pairs, print "NO" (without quotes).

Otherwise print "YES" (without quotes) in the first line and the edges of the tree in the next n−1n−1 lines. Each of the last n−1n−1 lines should contain two integers xixi and yiyi (1≤xi,yi≤n1≤xi,yi≤n) — vertices connected by an edge.

Note: The numeration of edges doesn't matter for this task. Your solution will be considered correct if your tree produces the same pairs as given in the input file (possibly reordered). That means that you can print the edges of the tree you reconstructed in any order.

题目大意

现有一棵树。用$n-1$个二元组(x,y)描述树上每条边，表示：删去这条边后，两个连通块内分别最大的编号。

问是否存在一颗符合描述的树。

题目分析

菊花图构造

注意到树被分为两个连通块后，产生的二元组(x,y)中必定有一个元素为$n$.

那么，有多少个二元组$(x,y)(y=n)$就说明有多少条边满足：$[x+1,n]$这些点和$x$点分别在被割断的两块。

树有一个性质：两点间的路径唯一。那么为了割断$x$和$[x+1]...n$，这两个连通块只能有唯一路径，并且路径上的点都必须小于$x$。于是这里有了一种对于单个点$x$的构造方法。那么其他点应该如何考虑？是应该在做出来的路径上分叉还是新开一条？

构造题可以说分为两类：唯一解和多解。这种多解的题，当然选一种最简洁的构造方法。事实上这样对于单点做下去，构造菊花图的方式就是合法的。

我们对于构造菊花图的担忧主要在于，要是每次都新开一条路径，会不会浪费了一些点？换而言之，原先的路径上能不能够共用一些点？

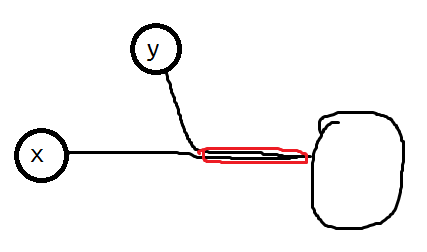
然而，共用路径上的边无论如何只会贡献一种二元组。如果共用，为了达到给定的二元组数量，也只能在原先路径上插上一条可独立的完整路径————也就是说相当于没有共用。

 #include<bits/stdc++.h>

 const int maxn = ;

 int n;

 bool used[maxn];

 int mp[maxn][maxn];

 int edgeTot,edges[maxn<<],nxt[maxn<<],head[maxn];

 int read()

 {

     char ch = getchar();

     int num = ;

     bool fl = ;

     for (; !isdigit(ch); ch=getchar())

         if (ch=='-') fl = ;

     for (; isdigit(ch); ch=getchar())

         num = (num<<)+(num<<)+ch-;

     if (fl) num = -num;

     return num;

 }

 void errorDown()

 {

     puts("NO");

     exit();

 }

 void addedge(int u, int v)

 {

     edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;

     edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot;

 }

 void dfs(int x, int fa)

 {

     for (int i=head[x]; i!=-; i=nxt[i])

     {

         int v = edges[i];

         if (v!=fa) printf("%d %d\n",x,v), dfs(v, x);

     }

 }

 int main()

 {

     n = read();

     memset(head, -, sizeof head);

     for (int i=; i<n; i++)

     {

         int u = read(), v = read();

         if (u > v) std::swap(u, v);

         if (v!=n) errorDown();

         mp[u][v]++;

     }

     for (int i=; i<n; i++)

         if (mp[i][n]){

             if (i < mp[i][n]) errorDown();

             used[i] = ;

             int lst = i, cnt = ;

             for (int j=; j<i&&cnt<mp[i][n]-; j++)

                 if (!used[j]){

                     used[j] = ;

                     addedge(lst, j);

                     lst = j;

                     cnt++;

                 }

             if (cnt!=mp[i][n]-) errorDown();

             addedge(lst, n);

         }

     puts("YES");

     dfs(, );

     return ;

 }

链构造

上一个做法的最后一段话并不是说不能构造出合法链。事实上可发现，刻意把小的节点接在大节点后也是可以的。

这里介绍一种非常巧妙的链构造：将$a_i$视作前缀最大值，由此构造一条链。

具体的证明和代码见题解 CF1041E 【Tree Reconstruction】

END