树链剖分【p2568】[SDOI2011]染色

Description

给定一颗有\(n\)个节点的无根树和\(m\)个操作,操作有\(2\)类：

• 1.将节点\(a\)到节点\(b\)路径上所有点染成颜色\(c\)
• 2.询问节点\(a\)到节点\(b\)路径上的颜色段数量(连续相同颜色被认为是同一段),如“112221”由三段组成："11","222"和“1”

请你写一个程序依次完成这\(m\)个操作.

Input

第一行包含两个整数\(n\)和\(m\),分别表示节点数和操作数.

第二行包含\(n\)个正整数表示\(n\)个节点的初始颜色.

下面\(n-1\)行每行包含两个整数\(x\)和\(y\)，表示\(x\)和\(y\)之间有一条无向边.

下面\(m\)行每行描述一个操作：

"C a b c",表示这是一个染色操作,把节点\(a\)到节点\(b\)路径上所有点(包括\(a\)和\(b\))都染成颜色\(c\)

“Q a b”表示这是一个询问操作,询问节点\(a\)到节点\(b\)(包括\(a\)和\(b\))路径上的颜色段数量.

Output

对于每个询问操作，输出一行答案。

很明显,这是一个树剖题.

但是维护起来会很麻烦.qwq

首先明确我们的线段树需要维护什么东西.

1. 我们需要维护颜色段的个数(题目要求啊,(#`O′))

由于线段树是每次将区间分成一半,所以我们需要考虑拼接。

因此我们需要维护的东西还有

1. 当前节点的左子区间中的颜色段
2. 当前节点的右子区间中的颜色段.

如果当前节点的左子区间的右子颜色段与当前节点的右子区间的左子颜色段相同,我们就需要拼接.(可能会有些难理解,请细细品读)

然后难点就在于剖分成链之后,我们跳转的时候,链顶与新的一部分的拼接.

这里以链的下端为\(L\),链的上端为\(R\),简单解释一下.

其中红色部分为已知部分的链,黑色部分为当前所求.

很容易发现,如果要拼接,我们需要将黑色部分左右端点调换,直接\(swap\)即可.

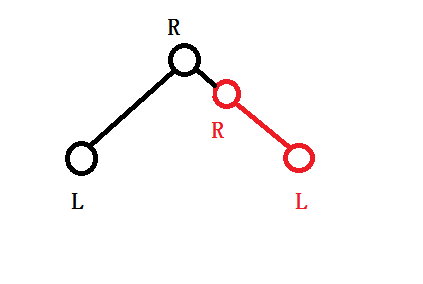
最后需要考虑的是当两端点在一条链上如何拼接,这里不再讨论,

请大家独立思考QwQ

本来应该一边切的,结果因为局部变量和重载出锅QAQ

代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cctype>
#define ls o<<1
#define rs o<<1|1
#define R register
#define N 300008
using namespace std;
inline void in(int &x)
{
    int f=1;x=0;char s=getchar();
    while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
    while(isdigit(s)){x=x*10+s-'0';s=getchar();}
    x*=f;
}
struct cod{int lc,rc,sum;}tr[N<<2];
cod operator +( cod a, cod b)
{
	cod res;
	res.lc=a.lc;res.rc=b.rc;
	res.sum=a.sum+b.sum;
	if(a.rc==b.lc)res.sum--;
	return res;
}
int n,m,head[N],tot,a[N],tg[N<<2];
struct code{int u,v;}edge[N<<2];
inline void add(int x,int y)
{
    edge[++tot].u=head[x];
    edge[tot].v=y;
    head[x]=tot;
}
int size[N],son[N],f[N],depth[N];
void dfs1(int u,int fa)
{
    depth[u]=depth[fa]+1;f[u]=fa;size[u]=1;
    for(R int i=head[u];i;i=edge[i].u)
    {
        if(edge[i].v==fa)continue;
        dfs1(edge[i].v,u);
        size[u]+=size[edge[i].v];
        if(son[u]==-1 or size[son[u]]<size[edge[i].v])
            son[u]=edge[i].v;
    }
}
int dfn[N],fdfn[N],idx,top[N];
void dfs2(int u,int t)
{
    dfn[u]=++idx;fdfn[idx]=u;top[u]=t;
    if(son[u]==-1)return;
    dfs2(son[u],t);
    for(R int i=head[u];i;i=edge[i].u)
    {
        if(dfn[edge[i].v])continue;
        dfs2(edge[i].v,edge[i].v);
    }
}
void build(int o,int l,int r)
{
    if(l==r)
    {
        tr[o].lc=tr[o].rc=a[fdfn[l]];
        tr[o].sum=1;
        return;
    }
    int mid=(l+r)>>1;
    build(ls,l,mid);
    build(rs,mid+1,r);
    tr[o]=tr[ls]+tr[rs];
}
inline void down(int o,int l,int r)
{
    if(tg[o])
    {
        tg[ls]=tr[ls].lc=tr[ls].rc=tg[o];
        tg[rs]=tr[rs].lc=tr[rs].rc=tg[o];
        tr[ls].sum=tr[rs].sum=1;
        tg[o]=0;
    }
}
void change(int o,int l,int r,int x,int y,int z)
{
    if(x<=l and y>=r)
    {
        tr[o].lc=tr[o].rc=tg[o]=z;
        tr[o].sum=1;
        return;
    }
    down(o,l,r);
    int mid=(l+r)>>1;
    if(x<=mid)change(ls,l,mid,x,y,z);
    if(y>mid)change(rs,mid+1,r,x,y,z);
    tr[o]=tr[ls]+tr[rs];
}
cod query(int o,int l,int r,int x,int y)
{
    if(x<=l and y>=r)return tr[o];
    down(o,l,r);
    int mid=(l+r)>>1;
    if(y<=mid)return query(ls,l,mid,x,y);
    if(x>mid)return query(rs,mid+1,r,x,y);
    return query(ls,l,mid,x,y)+query(rs,mid+1,r,x,y);
}
inline void tchange(int x,int y,int z)
{
    int fx=top[x],fy=top[y];
    while(fx!=fy)
    {
        if(depth[fx]>=depth[fy])
        {
            change(1,1,n,dfn[fx],dfn[x],z);
            x=f[fx];
        }
        else
        {
            change(1,1,n,dfn[fy],dfn[y],z);
            y=f[fy];
        }
        fx=top[x],fy=top[y];
    }
    if(dfn[x]>dfn[y])swap(x,y);
    change(1,1,n,dfn[x],dfn[y],z);
}
inline cod tquery(int x,int y)
{
    cod a,b,res;
    a.lc=a.rc=b.lc=b.rc=a.sum=b.sum=0;
    int fx=top[x],fy=top[y];
    while(fx!=fy)
    {
        if(depth[fx]>=depth[fy])
        {
            res=query(1,1,n,dfn[fx],dfn[x]);
            swap(res.lc,res.rc);
            a=a+res;
            x=f[fx];
        }
        else
        {
            res=query(1,1,n,dfn[fy],dfn[y]);
            swap(res.lc,res.rc);
            b=b+res;
            y=f[fy];
        }
        fx=top[x],fy=top[y];
    }
    if(dfn[x]>dfn[y])
    {
        swap(x,y);
        swap(a,b);
    }
    res=query(1,1,n,dfn[x],dfn[y]);
    a=a+res;
    swap(b.lc,b.rc);
    return a+b;
}
char s[8];
int main()
{
    in(n),in(m);memset(son,-1,sizeof son);
    for(R int i=1;i<=n;i++)in(a[i]);
    for(R int i=1,x,y;i<n;i++)
    {
        in(x),in(y);
        add(x,y),add(y,x);
    }
    dfs1(1,0);dfs2(1,1);build(1,1,n);
    for(R int a,b,c;m;m--)
    {
        scanf("%s",s+1);
        if(s[1]=='Q')
        {
            in(a),in(b);
            printf("%d\n",tquery(a,b).sum);
        }
        else
        {
            in(a),in(b),in(c);
            tchange(a,b,c);
        }
    }
}