线段tree~讲解+例题

最近学习了线段树这一重要的数据结构，有些许感触。所以写一篇博客来解释一下线段树，既是对自己学习成果的检验，也希望可以给刚入门线段树的同学们一点点建议。

首先声明一点，本人是个蒟蒻，如果在博客中有什么不当的地方，还请大佬们指出来，感激不尽！

一.为什么要用线段树？

既然线段树对于初学者来说，不是那么好学也不好写，那么为什么要用到线段树，是一个问题。

下面，我们先看一个问题：

100000个正整数，编号从1到100000，用A[1],A[2],A[100000]表示。
修改：1.将第L个数增加C （1 <= L <= 100000）

统计：1.编号从L到R的所有数之和为多少？ 其中1<= L <= R <= 100000.

我们很容易就想到暴力算法，但是在实现后，我们发现程序运行起来很慢。

那么有没有什么解决方法？答案当然是：线段树！

二.什么是线段树？

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。（摘自百度百科）

便于对一段元素的查询与修改。

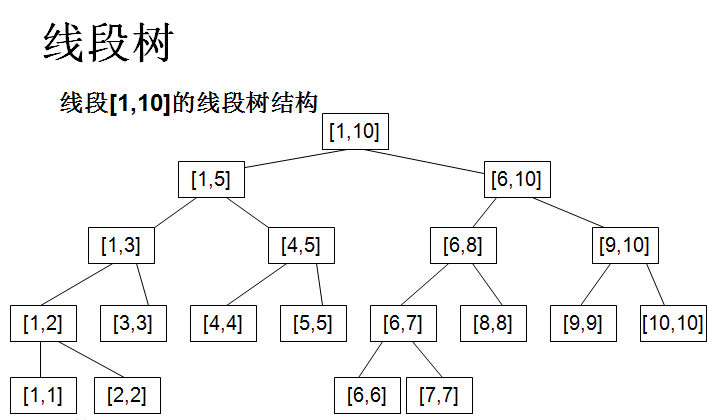
我们观察上图可以看出：

每一个叶子节点就是每个元素，每一个父节点都是对自己下面子节点的整合，而根节点就是对整个元素的整合。

学过分块的同学不难看出来，线段树就是在分块里面分块。

按理说分块能做的题，线段树绝大部分都能做，但是也有一部分题目所要求维护的元素信息是只有分块能维护的，在这里不细讲分块和线段树的区别，我们继续看线段树。

如果觉得我讲的不是很明白，在这里借用luogu 皎月半洒花（✿✿ヽ(°▽°)ノ✿）dalao的一段解释：

三.如何实现一颗线段树？

先说一下我的码风习惯：rt是当前节点，left是整棵树的左端点，right是右端点，mid是中点，l，r是代表要查询或者修改的区间范围，add是要更改的值，lson和rson我更喜欢在宏定义里搞定，build是递归建树，update是修改函数，query是查询函数，PushUP是上滤，PushDOWN是下滤

1.建造一颗线段树：

利用二叉树父子节点关系，父亲为i，孩子为2i+1,2i的特点，我们考虑递归建树（当然有其他更快的建树方法，在这里先不讲了）

在建树前，我们要先取出父节点的孩子，还需要一个PushUP函数来维护向上父子节点的关系。

在不同的要求下，PushUP的写法会不一样。这里以luogu P3372为例，PushUP函数的作用是求和。

 #define ll long long
 #define lson left, mid, rt<<1//左儿子
 #define rson mid+1, right, rt<<1|1//右儿子

 const int maxn = ;
 ll ans[maxn<<];//因为线段树所以要开四倍的空间
 void PushUP(ll rt)//在这里的作用是求和，维护父子节点关系的正常
 {
     ans[rt] = ans[rt<<] + ans[rt<<|];
 }
 void build(ll left, ll right, ll rt)
 {
     if(left == right)//如果到了叶子节点
     {
         cin>>ans[rt];//输入叶子节点元素，即所给的序列元素
         return;
     }
     ll mid = (left + right)>>;
     build(lson);//左右递归建树，并且维护上下父子关系
     build(rson);
     PushUP(rt);
 }

2.线段树的基本操作

这里列举几个基本的线段树操作：

（1）单点修改

这里的单点修改是把一个新的值付给某个序列中的元素。

 void update(ll s, ll add, ll left, ll right, ll rt)
 {
     if(left == right)
     {
         ans[rt] = add;
         return ;
     }
     ll mid = (left + right)>>;
     if(s <= mid) update(s, add, lson);
     else update(s, add, rson);
     PushUP(rt);
 }

（2）区间修改

因为是修改的是一个区间，所以我们会直接修改线段树中的父节点。于是我们需要一个下滤的操作，即PushDOWN，在这里我们为了让我们的线段tree跑的更快，我们引入了一个新的数组——lazy。（也可以叫染色col，但是我更喜欢懒标记这个叫法）懒标记实际上就是让子节点暂时处于不更新状态，用到的时候再更新。因为线段树的优点不在于全记录，而在于传递式记录。跑的才快。这里依旧是luogu P3372的区间修改，作用为给一段区间每个元素都加上一个数。

 void PushDOWN(ll rt, ll mid, ll left, ll right)
 {
     if(lazy[rt])
     {
         lazy[rt<<]+=lazy[rt];
         lazy[rt<<|]+=lazy[rt];
         ans[rt<<]+=(mid-left+)*lazy[rt];
         ans[rt<<|]+=(right-mid)*lazy[rt];//给线段树更新lazy标记的值，因为是修改区间，所以要乘元素个数
         lazy[rt]=;//lazy已经传递完，归零
     }
 }
 void update(ll l, ll r, ll add, ll left, ll right, ll rt)
 {
     if(l<=left&&r>=right)
     {
         lazy[rt]+=add;
         ans[rt]+=add*(right-left+);
         return;
     }
     ll mid = (left+right)>>;
     PushDOWN(rt,mid,left,right);//下滤更改元素值
     //这里注意判断左右子树跟[l,r]有无交集，有交集才递归
     if(l<=mid) update(l,r,add,lson);
     if(r>mid)  update(l,r,add,rson);
     PushUP(rt);//更新当前节点信息
 }

（3）区间查询

区间查询l到r的和，返回res

ll query(ll l, ll r, ll left, ll right, ll rt)//这里变量的意义是查询l到r，左区间为left到mid，右区间为mid+1到right
{
    ll res = ;
    if(l<=left&&r>=right)//在区间内直接返回
    {
        return ans[rt];
    }
    ll mid = (left + right)>>;
    PushDOWN(rt,mid,left,right);
    if(l<=mid) res += query(l,r,lson);//左子区间与[L,R]有重叠，递归
    if(r>mid) res += query(l,r,rson);//右子区间与[L,R]有重叠，递归
    return res;
}

至于单点查询，你知道区间还能不会单点嘛~

 四.线段树实战

1.luogu P3372 【模板】线段树1

区间修改，区间求和查询

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #define ll long long
 #define lson left, mid, rt<<1
 #define rson mid+1, right, rt<<1|1
 using namespace std;
 const int maxn = ;
 ll n, m, ans[maxn<<],lazy[maxn<<];
 void PushUP(ll rt)
 {
     ans[rt] = ans[rt<<] + ans[rt<<|];
 }
 void build(ll left, ll right, ll rt)
 {
     if(left == right)
     {
         cin>>ans[rt];
         return;
     }
     ll mid = (left + right)>>;
     build(lson);
     build(rson);
     PushUP(rt);
 }

 void PushDOWN(ll rt, ll mid, ll left, ll right)
 {
     if(lazy[rt])
     {
         lazy[rt<<]+=lazy[rt];
         lazy[rt<<|]+=lazy[rt];
         ans[rt<<]+=(mid-left+)*lazy[rt];
         ans[rt<<|]+=(right-mid)*lazy[rt];
         lazy[rt]=;
     }
 }
 ll query(ll l, ll r, ll left, ll right, ll rt)
 {
     ll res = ;
     if(l<=left&&r>=right)
     {
         return ans[rt];
     }
     ll mid = (left + right)>>;
     PushDOWN(rt,mid,left,right);
     if(l<=mid) res += query(l,r,lson);
     if(r>mid) res += query(l,r,rson);
     return res;
 }
 void update(ll l, ll r, ll add, ll left, ll right, ll rt)
 {
     if(l<=left&&r>=right)
     {
         lazy[rt]+=add;
         ans[rt]+=add*(right-left+);
         return;
     }
     ll mid = (left+right)>>;
     PushDOWN(rt,mid,left,right);
     if(l<=mid) update(l,r,add,lson);
     if(r>mid)  update(l,r,add,rson);
     PushUP(rt);
 }

 int main()
 {
     cin.sync_with_stdio(false);
     cin>>n>>m;
     ll p,x,y,k;
     build(,n,);
     while(m--)
     {
         cin>>p;
         if(p==)
         {
             cin>>x>>y>>k; update(x,y,k,,n,);
         }
         if(p==)
         {
             cin>>x>>y;    cout<<query(x,y,,n,)<<endl;
         }
     }
     return ;
 }

2.luogu P1531 I Hate It

单点修改，区间最值查询

此题注意一点，对于是否确定修改，我们可以用max来搞定

 #include <cstdio>
 #include <algorithm>
 #include <iostream>
 #define lson left, mid, rt<<1
 #define rson mid+1, right, rt<<1|1
 #define ll long long
 using namespace std;
 const int maxn =  + ;
 ll n, m, a[maxn], ans[maxn<<];
 inline void PushUP(ll rt)
 {
     ans[rt] = max(ans[rt<<],ans[rt<<|]);
 }

 void build(ll left, ll right, ll rt)
 {
     if(left == right) {scanf("%d",&ans[rt]); return ;}
     ll mid = (left + right)>>;
     build(lson);
     build(rson);
     PushUP(rt);
 }
 void update(ll s, ll add, ll left, ll right, ll rt)
 {
     if(left == right)
     {
         ans[rt] = max(add,ans[rt]);
         return ;
     }
     ll mid = (left + right)>>;
     if(s <= mid) update(s, add, lson);
     else update(s, add, rson);
     PushUP(rt);
 }
 ll query(ll l, ll r, ll left, ll right, ll rt)
 {

     if(l <= left&&right <= r){return ans[rt];}
     ll mid = (left + right)>>;
     ll res = ;
     if(l <= mid) res = max(res,query(l, r, lson));
     if(r > mid)  res = max(res,query(l, r, rson));
     return res;
 }
 int main()
 {
     int a,b;
     char c;
     scanf("%lld%lld", &n, &m);
     build(,n,);
     for(int i = ; i <= m; i++)
     {
         cin>>c;
         if(c == 'U')
         {
             cin>>a>>b;
             update(a,b,,n,);
         }
         if(c == 'Q')
         {
             cin>>a>>b;
             printf("%lld\n",query(a,b,,n,));
         }
     }
     return ;
 } 

3.luogu P2068 统计和

单点修改 区间求和查询

 #include <cstdio>
 #include <iostream>
 #define lson left , mid , rt << 1
 #define rson mid + 1 , right , rt << 1 | 1
 using namespace std;
 const int maxn = ;
 int sum[maxn<<];
 void PushUP(int rt) {
         sum[rt] = sum[rt<<] + sum[rt<<|];
 }
 void build(int left,int right,int rt) {
         if (left == right) {
                 sum[rt] = ;//我们干脆直接建一颗所有初始元素都是0的线段树
                 return ;
         }
         int mid = (left + right) >> ;
         build(lson);
         build(rson);
         PushUP(rt);
 }
 void update(int p,int add,int left,int right,int rt) //在p位置上增加add
 {
         if (left == right) {
                 sum[rt] += add;
                 return ;
         }
         int mid = (left + right) >> ;
         if (p <= mid) update(p , add , lson);
         else update(p , add , rson);
         PushUP(rt);
 }
 int query(int l,int r,int left,int right,int rt) {
         if (l <= left && right <= r) {
                 return sum[rt];
         }
         int mid = (left + right) >> ;
         int res = ;
         if (l <= mid) res += query(l , r , lson);
         if (r > mid) res += query(l , r , rson);
         return res;
 }
 int main() {
         int m , n;
                 scanf("%d%d",&n,&m);
                 build( , n , );
                 char x;
                 while (m--) {
                         cin>>x;
                         int a , b , c;

                         if (x == 'y') {
                             scanf("%d%d",&a,&b);
                             printf("%d\n",query(a , b ,  , n , ));
                         }
                         else {
                             scanf("%d%d",&a,&c);
                             update(a , c ,  , n , );
                         }
                 }
         return ;
 }

当然还有很多的线段树例题。但是我不建议用线段树去做luogu P1816 忠诚，那个题我觉得更适合ST表，因为是裸的RMQ，而且你线段树如果没有优化跑不快会被卡。

这里我讲的只是关于线段树很基本的一些东西，关于线段树，还有很多很多，比如二维线段树，重口味zkw线段树，各种各样的优化，不用递归建树等等等等......

希望对线段树初学者能有所帮助，如果我写的有不对的地方，希望大佬能指出。

最后推荐几个博客，也是对线段树的讲解：

http://blog.csdn.net/zearot/article/details/52280189

http://blog.csdn.net/zearot/article/details/48299459

http://blog.csdn.net/kzzhr/article/details/10813301

最后特别推荐_pks luogu 皎月半洒花的一篇对线段树的讲解

https://pks-loving.blog.luogu.org/senior-data-structure-qian-tan-xian-duan-shu-segment-tree