uva10943(隔板法)
很裸的隔板法。
引用一下维基上对隔板法的解释:
现在有10个球,要放进3个盒子里
- ●●●●●●●●●●
隔2个板子,把10个球被隔开成3个部份
- ●|●|●●●●●●●●、●|●●|●●●●●●●、●|●●●|●●●●●●、●|●●●●|●●●●●、●|●●●●●|●●●●、●|●●●●●●|●●●、......
如此类推,10个球放进3个盒子的方法总数为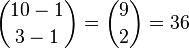
n个球放进k个盒子的方法总数为
问题等价于求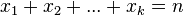 的可行解数,其中
的可行解数,其中 为正整数。
为正整数。
**如果允许有空盒子**:
现在有10个球,要放进3个盒子里,并允许空盒子。考虑10+3个球的情况:
- ●|●|●●●●●●●●●●●
从3个盒子里各拿走一个,得到一种情况,如此类推:
- ||●●●●●●●●●●、|●|●●●●●●●●●、|●●|●●●●●●●●、|●●●|●●●●●●●、|●●●●|●●●●●●、......
n个球放进k个盒子的方法总数(允许空盒子)为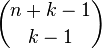 [2]
[2]
问题等价于求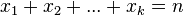 的可行解数,其中
的可行解数,其中 为非负整数。
为非负整数。
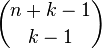 也是
也是 展开式的项数,这是因为展开后每一项肯定是a1^x1*a2^x2*......*ak^xk,而且x1+x2+...+xk=n.那就转化为上面那个问题了。
展开式的项数,这是因为展开后每一项肯定是a1^x1*a2^x2*......*ak^xk,而且x1+x2+...+xk=n.那就转化为上面那个问题了。
另一种变形:
减少球数用隔板法
将20个相同的小球放入编号分别为1,2,3,4的四个盒子中,要求每个盒子中的球数不少于它的编号数,求放法总数。
分析:先在编号1,2,3,4的四个盒子内分别放0,1,2,3个球,剩下14个无区别的球,问题等价于将14个球放入4个编号为1,2,3,4的四个盒子里,每个盒子至少有一个球的问题。
剩下14个无区别的球排成一列,共形成13个空,可以理解为有3块隔板,将排成一列的球隔成4段,每段至少1个,有C3/13=286(种)。
如果不用隔板法,亦可以递推来做:
按最后一个加上的数是几来分类,ans[n][k]=ans[n-1][k]+ans[n][k-1].其中ans[n][k-1]是最后一个加0,ans[n-1][k]是最后一位加的不是0.
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>
using namespace std;
#define INF 1000000000
#define eps 1e-8
#define pii pair<int,int>
#define LL long long int
const int mod=1000000;
int n,k,ans,c[250][250];
int main()
{
//freopen("in6.txt","r",stdin);
//freopen("out.txt","w",stdout);
c[0][0]=1;
for(int i=1;i<=200;i++)
{
c[i][0]=c[i][i]=1;
for(int j=1;j<i;j++)
{
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
while(scanf("%d%d",&n,&k)==2)
{
if(n==0&&k==0) break;
else
{
printf("%d\n",c[n+k-1][k-1]);
}
}
//fclose(stdin);
//fclose(stdout);
return 0;
}
uva10943(隔板法)的更多相关文章
- CF451E Devu and Flowers (隔板法 容斥原理 Lucas定理 求逆元)
Codeforces Round #258 (Div. 2) Devu and Flowers E. Devu and Flowers time limit per test 4 seconds me ...
- vijos1060 隔板法
排列组合问题 之前没有学过隔板法,随便学习了一下 其实挺好理解的 附上题解: 先只考虑一种球:因为有n个盒子每个盒子可以放任意多球,还可以空出来任意多球.所以可以考虑为n+1个盒子,最后一个盒子里面是 ...
- BZOJ 3028: 食物 [生成函数 隔板法 | 广义二项式定理]
3028: 食物 Time Limit: 3 Sec Memory Limit: 128 MBSubmit: 497 Solved: 331[Submit][Status][Discuss] De ...
- How do you add? UVA - 10943(组合数的隔板法!!)
题意: 把K个不超过N的非负整数加起来,使它们的和为N,有多少种方法? 隔板法...不会的可以买一本高中数学知识清单...给高中班主任打个广告.... 隔板法分两种...一种是不存在空集 = C(n- ...
- 51Nod 1509 加长棒(隔板法)
http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1509 思路: 直接去解可行的方法有点麻烦,所以应该用总的方法去减去不可行 ...
- hdu6397 Character Encoding 隔板法+容斥原理+线性逆元方程
题目传送门 题意:给出n,m,k,用m个0到n-1的数字凑出k,问方案数,mod一个值. 题目思路: 首先如果去掉数字范围的限制,那么就是隔板法,先复习一下隔板法. ①k个相同的小球放入m个不同的盒子 ...
- HDU4045 Machine scheduling —— 隔板法 + 第二类斯特林数
题目链接:https://vjudge.net/problem/HDU-4045 Machine scheduling Time Limit: 5000/2000 MS (Java/Others) ...
- 逆元 组合A(n,m) C(n,m)递推 隔板法
求逆元 https://blog.csdn.net/baidu_35643793/article/details/75268911 int inv[N]; void init(){ inv[] = ; ...
- light oj 1102 - Problem Makes Problem组合数学(隔板法)
1102 - Problem Makes Problem As I am fond of making easier problems, I discovered a problem. Actuall ...
随机推荐
- python基础实例
1.在Python 语言中,对象是通过引用传递的.在赋值时,不管这个对象是新创建的,还是一个已经存在的,都是将该对象的引用(并不是值)赋值给变量. 如:x=1 1这个整形对象被创建,然后将这个对象的引 ...
- Hub,bridge,switch and router的区别
首先说HUB,也就是集线器.它的作用可以简单的理解为将一些机器连接起来组成一个局域网.而交换机(又名交换式集线器)作用与集线器大体相同.但是两者在性能上有区别:集线器采用的式共享带宽的工作方式,而交换 ...
- django的模板系统过滤器笔记
-------------------django内建的过滤器-------------------1.add 使用形式为:{{ value | add: "2"}}意义:将val ...
- ACM解题之快速输出杨辉三角形(前68行)
题意: 本题要求计算并输出杨辉三角形的前 68 行. Time Limit:1000MS Memory Limit:65536K 解题: 为了能在规定时间准确输出杨辉三角形的前68行,这里我用了精准的 ...
- 剑指offer 面试17题
面试17题: 题目:打印从1到最大的n位数 题:输入数字n,按顺序打印出从1到最大的n位十进制数,比如输入3,则打印出1.2.3一直到最大的3位数999. 解题思路:需要考虑大数问题,这是题目设置的陷 ...
- LSTM梳理,理解,和keras实现 (一)
注:本文主要是在http://colah.github.io/posts/2015-08-Understanding-LSTMs/ 这篇文章的基础上理解写成,姑且也可以称作 The understan ...
- BGP Basic Knowledge
声明: 这篇文章是对网上的这几篇博客的摘录,仅供我自己以后看的时候方便,且不需要再看太多的内容, 如果大家对BGP不是很了解,建议看原博客或者直接看RFC BGP只支持基于目的地址的路由,即路 ...
- PAT 天梯赛 L1-026. I Love GPLT 【水】
题目链接 https://www.patest.cn/contests/gplt/L1-026 AC代码 #include <iostream> #include <cstdio&g ...
- hadoop06---多线程
.1.1. 实现线程的两种方式 1.继承Thread的方式 见代码MyThreadWithExtends 2.声明实现 Runnable 接口的方式 见代码MyThreadWithImpliment ...
- PHP 数字转大写
<?php header("content-type:text/html;charset=utf-8"); function numToRmb($num){ $rmbNum ...
