UICollectionViews有了简单的重排功能

代码地址如下：
http://www.demodashi.com/demo/13213.html

一、前言

我是UICollectionView的忠实粉丝。这个类比起它的老哥UITableView类具有更高的可定制性。现在我用collection view的次数要比用table view还多。随着iOS9的到来，它支持简单的重排。在此之前，重排不可能有现成的方法，同时这样做也是件痛苦的工作。现在让我们来看看API，你可以在下载本项目源码，看具体的实现过程。

二、实现过程

添加简单重排的最简单的方式是用UICollectionViewController。它现在有了一个新的属性叫installsStandardGestureForInteractiveMovement（为交互式移动工作设置标准手势），这个属性的添加使得我们可以用标准手势来对cell单元进行重新排序。该属性默认值为true，这意味着我们只需要重载一个方法就可以让它正常工作。

override func collectionView(collectionView: UICollectionView,
    moveItemAtIndexPath sourceIndexPath: NSIndexPath,
    toIndexPath destinationIndexPath: NSIndexPath) {
    // move your data order
}

Collection view推断每个item(元素)可以被移动，因为moveItemAtIndexPath函数被重载了。

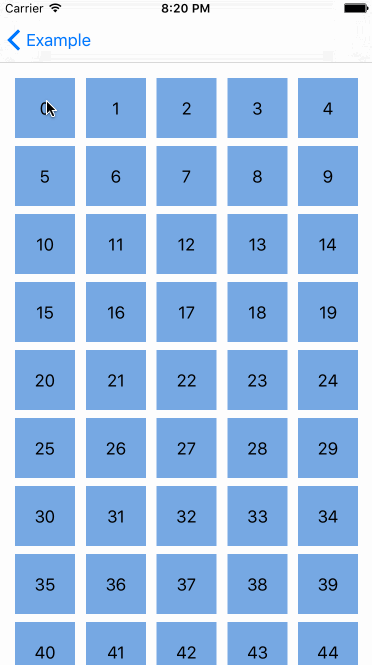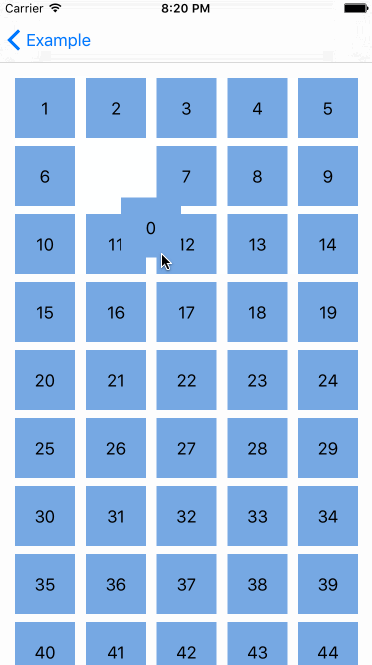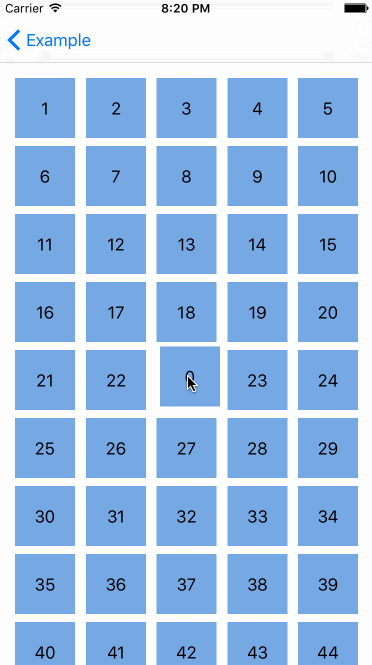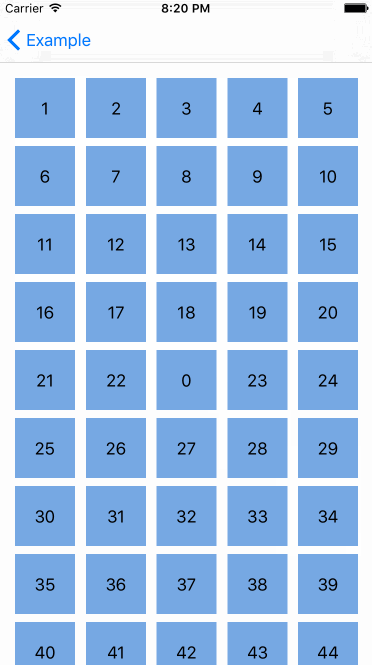
当我们想使用一个带有collection view的简单的UIViewController时，事情变得更加复杂。我们还需要实现之前提到的UICollectionViewDataSource的方法，但我们需要重写installsStandardGestureForInteractiveMovement。别担心，这些也很容易被支持。UILongPressGestureRecognizer是一个持续的、完全支持平移的手势识别器。

override func viewDidLoad() {
    super.viewDidLoad()

            longPressGesture = UILongPressGestureRecognizer(target: self, action: "handleLongGesture:")
        self.collectionView.addGestureRecognizer(longPressGesture)
}

    func handleLongGesture(gesture: UILongPressGestureRecognizer) {
        switch(gesture.state) {
        case UIGestureRecognizerState.Began:
            guard let selectedIndexPath = self.collectionView.indexPathForItemAtPoint(gesture.locationInView(self.collectionView)) else {
                break
            }
            collectionView.beginInteractiveMovementForItemAtIndexPath(selectedIndexPath)
        case UIGestureRecognizerState.Changed:
            collectionView.updateInteractiveMovementTargetPosition(gesture.locationInView(gesture.view!))
        case UIGestureRecognizerState.Ended:
            collectionView.endInteractiveMovement()
        default:
            collectionView.cancelInteractiveMovement()
        }
    }

我们储存了被选择的索引路径，这个路径从 longPressGesture handler（长按手势处理器）中获得，这个路径还取决于它是否有任何我们允许的，跟平移手势相关的值。接下来我们根据手势状态调用一些新的 collection view 方法：

• beginInteractiveMovementForItemAtIndexPath(indexPath: NSIndexPath)? 开始在特定的索引路径上对cell（单元）进行 Interactive Movement（交互式移动工作）。

• updateInteractiveMovementTargetPosition(targetPosition: CGPoint)? 在手势作用期间更新交互移动的目标位置。】

• endInteractiveMovement()? 在完成手势动作后，结束交互式移动

• cancelInteractiveMovement()? 取消 Interactive Movement。

这让处理平移手势更容易理解了。

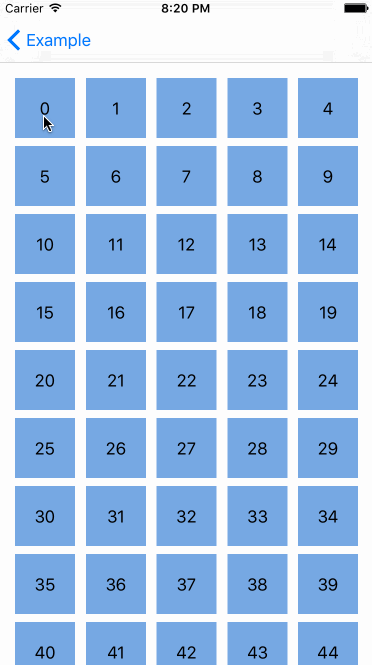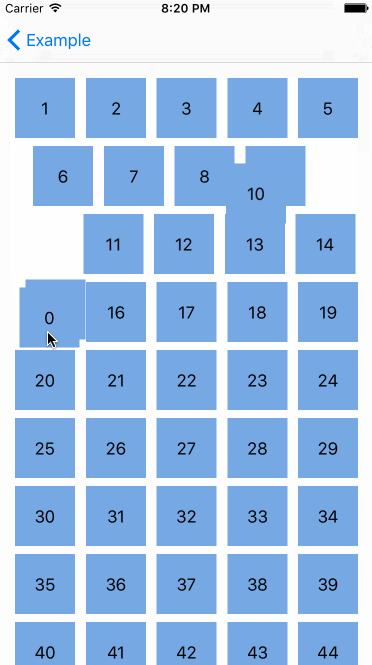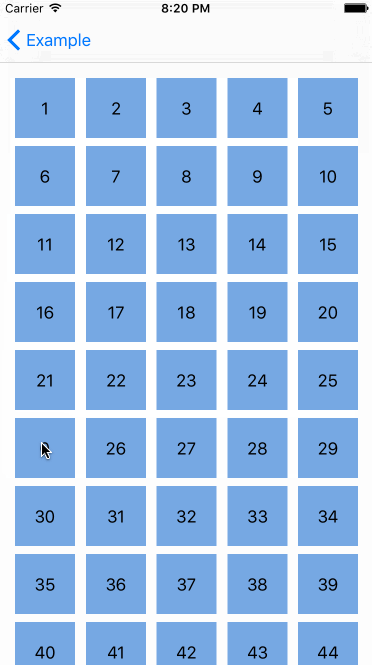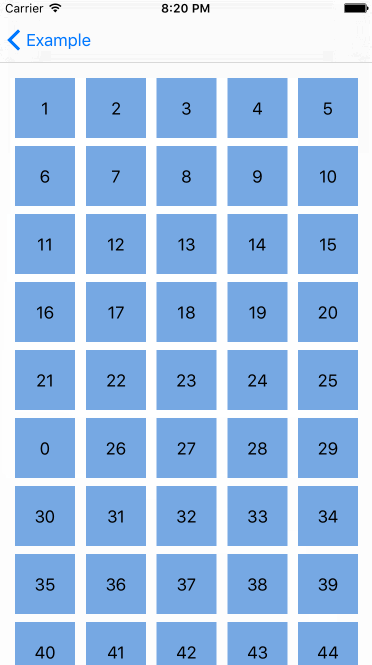
机器反应跟标准的 UICollectionViewController 一样，真的很酷，但是还有更酷的--我们能对自定义的 collection view layout（collection集合视图布局）申请重排，下面是在 waterfall layout（瀑布布局）里对 Interactive Movement 的测试。

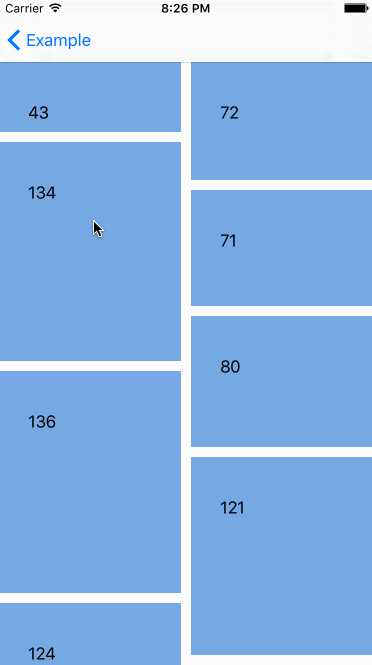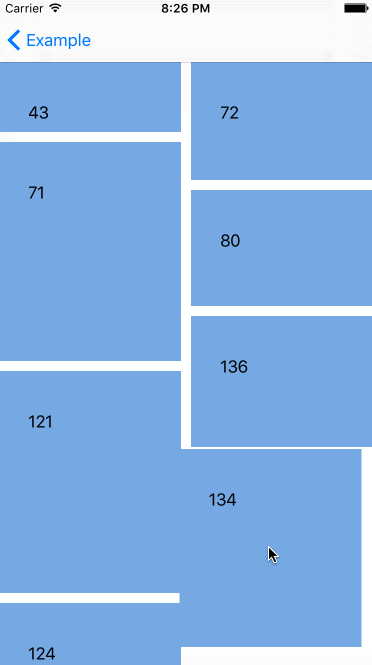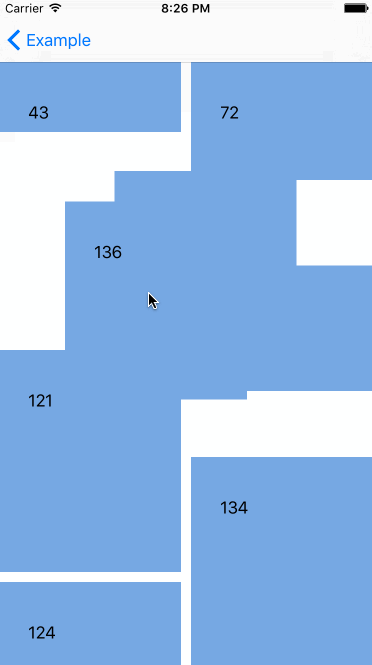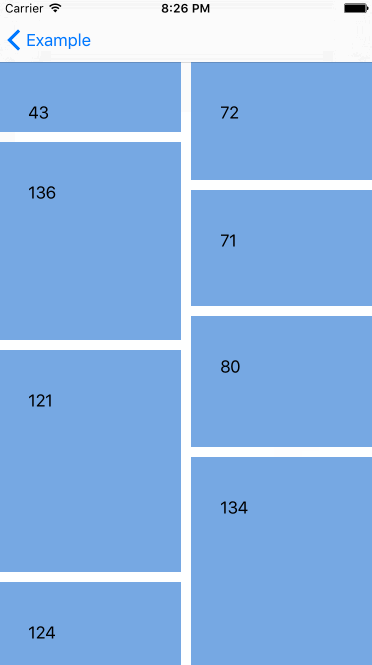
嗯哼，看起来很酷，但如果我们不想在移动 cell（单元）的时候改变它们的大小，那该怎么做？被选择的 cell（单元）的大小在 Interactive Movement 期间应该保持原样。这是可行的。UICollectionViewLayout 有附加的方法来处理重排。

func invalidationContextForInteractivelyMovingItems(targetIndexPaths: [NSIndexPath],
    withTargetPosition targetPosition: CGPoint,
    previousIndexPaths: [NSIndexPath],
    previousPosition: CGPoint) -> UICollectionViewLayoutInvalidationContext

func invalidationContextForEndingInteractiveMovementOfItemsToFinalIndexPaths(indexPaths: [NSIndexPath],
    previousIndexPaths: [NSIndexPath],
    movementCancelled: Bool) -> UICollectionViewLayoutInvalidationContext

第一个函数在元素的 Interactive Movement 期间被调用，它带有 target（目标元素）和先前的 cell 的indexPaths（索引地址）。第二个与第一个函数类似，但它只在 Interactive Movement 结束后才调用。通过这些知识我们能通过一点小窍门，实现我们的需求。

internal override func invalidationContextForInteractivelyMovingItems(targetIndexPaths: [NSIndexPath],
    withTargetPosition targetPosition: CGPoint,
    previousIndexPaths: [NSIndexPath],
    previousPosition: CGPoint) -> UICollectionViewLayoutInvalidationContext {

    var context = super.invalidationContextForInteractivelyMovingItems(targetIndexPaths,
        withTargetPosition: targetPosition, previousIndexPaths: previousIndexPaths,
        previousPosition: previousPosition)

    self.delegate?.collectionView!(self.collectionView!, moveItemAtIndexPath: previousIndexPaths[0],
        toIndexPath: targetIndexPaths[0])

    return context
}

取得当前正在移动的cell的之前的和目标索引路径，然后调用 UICollectionViewDataSource 方法来移动这些 item（元素）。

毫无疑问，collection view的重排是一个出色的附加功能，UIKit前端框架工程师干得漂亮！