The Shortest Statement(Educational Codeforces Round 51 (Rated for Div.2)+最短路+LCA+最小生成树)

题目链接

传送门

题面

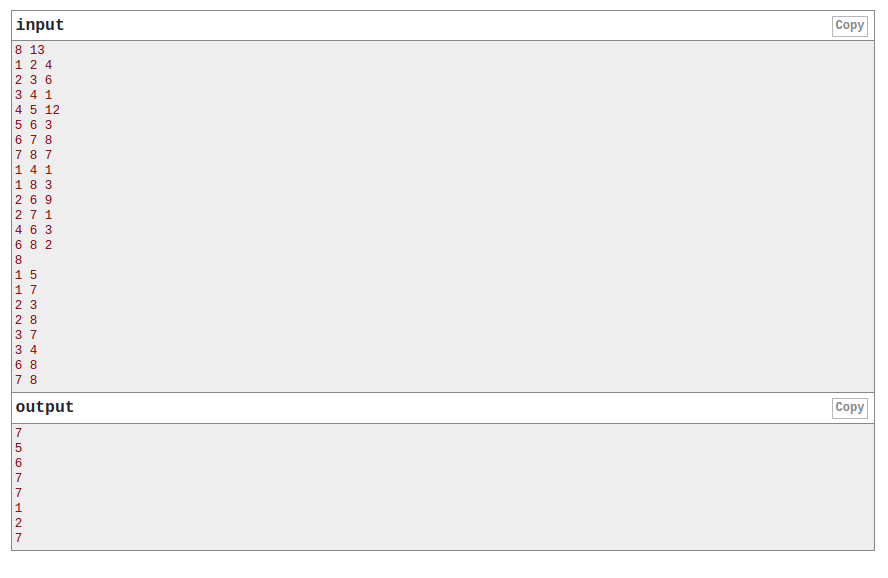
题意

给你一张有\(n\)个点\(m\)条边的联通图(其中\(m\leq n+20)\)，\(q\)次查询，每次询问\(u\)与\(v\)之间的最短路。

思路

由于边数最多只比点数大21，因此我们可以先跑出一棵最小生成树，然后将非树上边的两个端点跑一边最短路，然后每次查询就比较\(max((dis[u]+dis[v]-2dis[lca(u,v)]),dist[i][u]+dis[i][v])\)，其中\(dis[u]\)表示\(u\)到最小生成树根节点的距离，\(dist[i][u]\)表示第\(i\)个点到\(u\)的最短路，其中\(i\)为非树边的某个端点。

代码实现如下

#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> piL;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;

#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("in","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)

const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;

int n, m, tot, u, v, q;
set<int> s;
set<int>::iterator it;
int fa[maxn], vis[maxn], head[maxn];
LL dis[45][maxn];

struct node {
    int u, v, w;
    bool operator < (const node& x) const {
        return w < x.w;
    }
}pp[maxn];

struct edge {
    int v, w, next;
}ed[maxn<<1];

void init() {
    tot = 0;
    for(int i = 0; i <= n; i++) {
        head[i] = -1;
        fa[i] = i;
    }
}

void add(int u, int v, int w) {
    ed[tot].v = v;
    ed[tot].w = w;
    ed[tot].next = head[u];
    head[u] = tot++;
}

struct LCA {
    int tot;
    int deep[maxn], fa[maxn][30], head[maxn];
    LL cost[maxn];
    struct edge {
        int v, w, next;
    }ed[maxn<<1];

    void init() {
        tot = 0;
        for(int i = 0; i <= n; i++) {
            head[i] = -1;
            cost[i] = deep[i] = 0;
        }
    }

    void add(int u, int v, int w) {
        ed[tot].v = v;
        ed[tot].w = w;
        ed[tot].next = head[u];
        head[u] = tot++;
    }

    void dfs(int u, int d, int p) {
        deep[u] = d, fa[u][0] = p;
        for(int i = head[u]; ~i; i = ed[i].next) {
            int v = ed[i].v;
            if(v == p) continue;
            cost[v] = cost[u] + ed[i].w;
            dfs(v, d + 1, u);
        }
    }

    void lca() {
        for(int i = 1; i <= n; i++) {
            for(int j = 1; (1<<j) <= n; j++) {
                fa[i][j] = -1;
            }
        }
        for(int j = 1; (1<<j) <= n; j++) {
            for(int i = 1; i <= n; i++) {
                if(fa[i][j-1] != -1) {
                    fa[i][j] = fa[fa[i][j-1]][j-1];
                }
            }
        }
    }

    int query(int u, int v) {
        if(deep[u] <= deep[v]) swap(u, v);
        int k;
        for(k = 0; (1 << (1 + k)) <= deep[u]; k++);
        for(int i = k; i >= 0; i--) {
            if(deep[u] - (1<<i) >= deep[v]) {
                u = fa[u][i];
            }
        }
        if(u == v) return u;
        for(int i = k; i >= 0; i--) {
            if(fa[u][i] != -1 && fa[u][i] != fa[v][i]) {
                u = fa[u][i], v = fa[v][i];
            }
        }
        return fa[u][0];
    }

    LL dis(int u, int v) {
        return cost[u] + cost[v] - 2 * cost[query(u, v)];
    }
}L;

void dij(int s, int num) {
    for(int i = 1; i <= n; ++i) {
        dis[num][i] = INF, vis[i] = 0;
    }
    priority_queue<pLi, vector<pLi>, greater<pLi> > q;
    dis[num][s] = 0;
    q.push({0, s});
    int u, v;
    while(!q.empty()) {
        u = q.top().second; q.pop();
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i = head[u]; ~i; i = ed[i].next) {
            v = ed[i].v;
            if(dis[num][v] > dis[num][u] + ed[i].w) {
                dis[num][v] = dis[num][u] + ed[i].w;
                q.push({dis[num][v], v});
            }
        }
    }
}

int fi(int x) {
    return fa[x] == x ? x : fa[x] = fi(fa[x]);
}

void kruskal() {
    sort(pp + 1, pp + m + 1);
    for(int i = 1; i <= m; ++i) {
        int p1 = fi(pp[i].u), p2 = fi(pp[i].v);
        if(p1 == p2) continue;
        fa[p1] = p2;
        vis[i] = 1;
    }
}

int main() {
#ifndef ONLINE_JUDGE
    FIN;
#endif
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; ++i) {
        scanf("%d%d%d", &pp[i].u, &pp[i].v, &pp[i].w);
    }
    init();
    kruskal();
    L.init();
    for(int i = 1; i <= m; ++i) {
        if(vis[i]) L.add(pp[i].u, pp[i].v, pp[i].w), L.add(pp[i].v, pp[i].u, pp[i].w);
        else s.insert(pp[i].u), s.insert(pp[i].v);
        add(pp[i].u, pp[i].v, pp[i].w), add(pp[i].v, pp[i].u, pp[i].w);
    }
    L.dfs(1, 0, 0);
    L.lca();
    int num = 0;
    for(it = s.begin(); it != s.end(); ++it) dij(*it, num++);
    scanf("%d", &q);
    while(q--) {
        scanf("%d%d", &u, &v);
        LL ans = L.dis(u, v);
        for(int i = 0; i < num; ++i) {
            ans = min(ans, dis[i][u] + dis[i][v]);
        }
        printf("%lld\n", ans);
    }
    return 0;
}