Codeforces Round 563 (Div. 2) 题解

自己开了场镜像玩。

前三题大水题。D有点意思。E完全不会。F被题意杀了……然而还是不会。

不过看过（且看懂）了官方题解，所以这里是六题题解齐全的。

---

A

水题。给原序列排序，如果此时合法则直接输出，否则说明所有数相同，一定无解。

时间复杂度 $O(n\log n)$。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int maxn=;
#define MP make_pair
#define PB push_back
#define lson o<<1,l,mid
#define rson o<<1|1,mid+1,r
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline ll read(){
    char ch=getchar();ll x=,f=;
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
int n,a[maxn],s1,s2;
int main(){
    n=read();
    FOR(i,,*n) a[i]=read();
    sort(a+,a+*n+);
    FOR(i,,n) s1+=a[i];
    FOR(i,n+,*n) s2+=a[i];
    if(s1==s2) printf("-1\n");
    else FOR(i,,*n) printf("%d ",a[i]);
}

---

B

水题。

首先，如果所有数的奇偶性都相同，那我们什么都不能做。

否则，如果两个数奇偶性不同，可以直接交换；如果两个数奇偶性相同，可以用一个奇偶性不同的作为中介交换。那么实际上就是任意两个数都能交换，排个序即可。

时间复杂度 $O(n\log n)$。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int maxn=;
#define MP make_pair
#define PB push_back
#define lson o<<1,l,mid
#define rson o<<1|1,mid+1,r
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline ll read(){
    char ch=getchar();ll x=,f=;
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
int n,a[maxn];
bool hhh[];
int main(){
    n=read();
    FOR(i,,n) a[i]=read(),hhh[a[i]&]=true;
    if(hhh[] && hhh[]) sort(a+,a+n+);
    FOR(i,,n) printf("%d ",a[i]);
}

---

C

水题。

首先质数位置的值互不相同。一一编号即可。

对于合数（设为 $x$），可以任取它的一个质因子（设为 $p$），令 $a_x=a_p$。此时序列最大值不变，而两个互质的数的位置的值不可能相同。

我取的是最小质因子。

时间复杂度 $O(n)$。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int maxn=;
#define MP make_pair
#define PB push_back
#define lson o<<1,l,mid
#define rson o<<1|1,mid+1,r
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline ll read(){
    char ch=getchar();ll x=,f=;
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
int n,ans[maxn],pr[maxn],mn[maxn],pl,cnt;
bool vis[maxn];
int main(){
    n=read();
    FOR(i,,n){
        if(!vis[i]) pr[++pl]=i,ans[i]=++cnt;
        FOR(j,,pl){
            if(i*pr[j]>n) break;
            vis[i*pr[j]]=true;
            mn[i*pr[j]]=pr[j];
            if(i%pr[j]==) break;
        }
    }
    FOR(i,,n) if(mn[i]) ans[i]=ans[mn[i]];
    FOR(i,,n) printf("%d ",ans[i]);
}

---

D

有一点点小难度，但还是很水。

首先考虑这个序列的前缀异或和 $S$。那么对于任意的 $i$，有 $S_i\ne x$；对于任意的 $i,j$（$i\ne j$），有 $S_i\oplus x\ne S_j$。

看第二条限制，发现如果选了 $a$，那么不能选 $a\oplus x$；如果选了 $a\oplus x$，那么不能选 $a$。对其它数没有影响。

所以可以在 $a,a\oplus x$ 中任选一个作为前缀异或和。

最后用选出来的前缀异或和算出原序列。此时答案一定是最优。

时间复杂度 $O(2^n)$。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int maxn=;
#define MP make_pair
#define PB push_back
#define lson o<<1,l,mid
#define rson o<<1|1,mid+1,r
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline ll read(){
    char ch=getchar();ll x=,f=;
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
int n,x,lim,ans[maxn],al;
bool vis[maxn];
int main(){
    n=read();x=read();
    lim=<<n;
    FOR(i,,lim-){
        if(vis[i^x] || i==x) continue;
        vis[i]=true;
        ans[++al]=i;
    }
    printf("%d\n",al);
    FOR(i,,al) printf("%d ",ans[i]^ans[i-]);
}

---

E

太难了……难度 2500……

为此专门另开了篇博客：传送门

---

F

一开始以为不会给树的形态，一直在想……

这里给出轻重链剖分（俗称树剖）的做法。

首先一开始肯定要查询 $1$ 到 $x$ 的距离。这个就是 $x$ 的深度 $dep_x$。（定义 $1$ 的深度为 $0$）

现在假设我们已经确定 $x$ 在 $u$ 的子树中。一开始 $u=1$。

我们沿着 $u$ 的重儿子一直跳，跳到叶子结点 $v$。（实际上不用真跳，可以实现成 $O(1)$）

接下来，再考虑 $y=lca(x,v)$。（从官方题解盗张图）

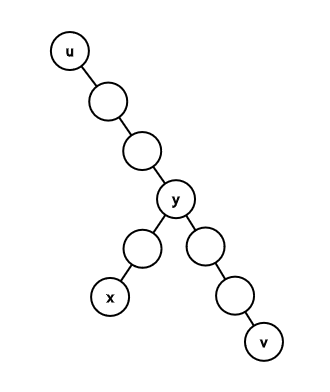
首先，询问一次 $dis(x,v)$。由于 $dis(x,v)=dep_x+dep_v-2dep_y$，而 $dis(x,v)$ 已知，$dep_x$ 已知，$dep_v$ 已知，可以算出 $dep_y$。那么 $y$ 也已知。

如果 $dep_x=dep_y$ 那么 $x=y$。 否则我们再询问 $y$ 到 $x$ 路径上的第二个点 $www$（没名字了），然后接下来就可以在 $u=www$ 的子树中寻找答案了。

对于最后一次查找，只用 $1$ 次询问，其它要 $2$ 次询问。预处理 $dep_x$ 要 $1$ 次询问。由于 $sz[www]\le sz[y]/2\le sz[u]$，所以每次 $u$ 的大小都会缩小一半。

那么总共要 $2\log n$ 次询问。时间复杂度 $O(n)$。

代码咕着，会来补的。