【神奇性质】【P5523】D [yLOI2019] 珍珠

D [yLOI2019] 珍珠

Description

给定一个 deque，要求支持 push_back 和 push_front 操作，并且查询前缀与非和以及后缀与非和。

deque中只会有 \(0\) 或 \(1\)，一共有 \(n\) 次操作，其中有 \(m\) 次操作给定，剩下的操作随机。

Limitations

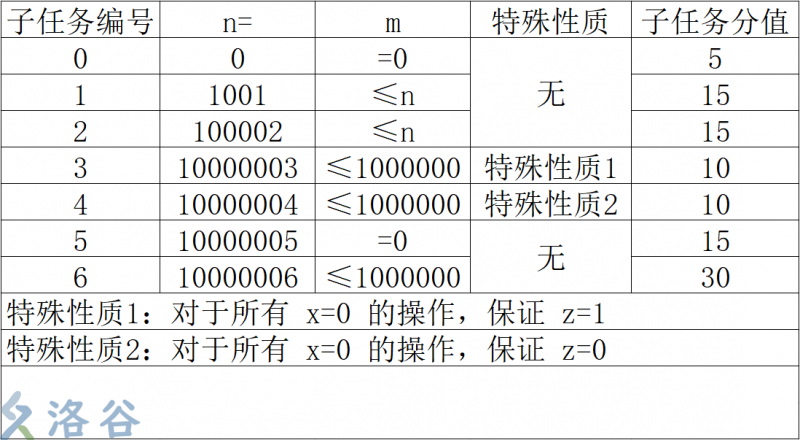
Solution

这是一道通过输入格式来防AK的题目

下面的做法只考虑前缀与非和，因为后缀的做法与前缀完全相同。

子任务 \(0\)：

没有操作，输出四个 \(0\) 即可。期望得分 \(5~pts\)

子任务 \(1\)：

暴力模拟，每次从前面插入的时候后面的元素暴力移位，暴力查询与非和即可。时间复杂度 \(O(n^2)\)，期望得分 \(15~pts\)

子任务 \(2\)：

考虑用线段树来维护每个区间的与非和，但是这样产生了一个问题，两个区间的与非和是无法合并的，因为与非运算没有交换律和结合律。

但是我们注意到事实上对于某个区间，序列的首部到区间左端点之前所有元素的与非和只可能是 \(0\) 或 \(1\)，因此线段树每个节点维护两个信息：当该区间之前所有元素的与非和是 \(0\) 时与非上该区间的值，以及当该区间之前元素与非和是 \(1\) 时与非上该区间的值，然后即可 \(O(1)\) 转移。

时间复杂度 \(O(n \log n)\)，期望得分 \(15 ~pts\)

子任务 \(3\)：

插入的元素全部是 \(1\)。

考虑一堆连续 \(1\) 的前缀与非和序列，一定形如 \(101010101\dots\)

证明上，考虑第一个位置一定是 \(1\)，然后 \(1~\text{nand}~1~=~0\) ，\(0~\text{nand}~1~=~1\)，因此序列中 \(0\) 和 \(1\) 一定是循环出现的。

因此一个询问的答案一定是 \(y~\&~1\)。时间复杂度 \(O(n)\)，期望得分 \(10~pts\)

子任务 \(4\)：

插入的元素全部是 \(0\)。

考虑一堆 \(0\) 的前缀与非和序列，一定形如 \(011111111111 \dots\)

用与子任务 \(3\) 类似的办法即可解决。时间复杂度 \(O(n)\)，期望得分 \(10~pts\)

子任务 \(5\)：

考虑一个显而易见的事实，\(0\) 与非任何数都得 \(1\)。

因此考虑一次查询如果与非和的最后一项是 \(0\)，则直接返回 \(1\) 即可。

同时对于最后一项是 \(1\) 的操作，只需要看这一项向前一共有连续的几个 \(1\)，由于前面那一项是 \(0\)，所以一段 \(011111\) 的序列的与非和一定是 \(1010101010\dots\)，而与 \(0\) 前面的项完全无关。

当然需要特判查询的 \(0\) 是序列第一个元素，以及查询的 \(1\) 前面没有 \(0\) 的情况。

那么问题就变成了对于每个位置维护它前面第一个 \(0\) 的位置。

由于 \(m = 0\) ，序列中的元素是完全随机的，因此连续 \(0/1\) 段的长度期望都是常数级的，因此暴力找即可，期望时间复杂度 \(O(n)\)，期望得分 \(15~pts\)

子任务 \(6\)：

考虑在序列不随机时怎么对每个数维护它前面第一个 \(0\) 的位置。

事实上，在每插入一个 \(0\) 时，都暴力修改这个 \(0\) 的有元素的一侧的连续 \(1\) 的信息即可。

例如，在序列左侧插入一个 \(0\)，则暴力修改 \(0\) 右侧连续 \(1\) 的左侧最近的 \(0\) 的位置为该位置即可。在序列右侧插入同理。

考虑时间复杂度：每个为 \(1\) 的元素都只会在左侧最近和右侧最近的 \(0\) 插入的时候被修改信息，因此每个元素都只会被修改 \(O(1)\) 次信息，即每次均摊修改 \(O(1)\) 个信息，总的修改次数为 \(O(n)\)，因此总时间复杂度 \(O(n)\)，期望得分 \(30~pts\)。

appreciation

感谢@Burnside 神仙帮助进行题解的校对工作