https://www.cnblogs.com/31415926535x/p/11611801.html

偶然看到的这个东西，可以说是第一次见到图论+数据结构的题了，，这题代码很简单，细节处理一下就没啥了，，，主要是一步一步的思路的推导很不错，，

cf-786 Legacy

以前做过的图论题就只是图论题，从来没想过和数据结构-线段树扯上关系，，

这题也算是一个经典的例题了吧，，应该就是那种知道的做过的就会做出来的类型，，

思路分析

题意很简单，就是一个简单的图，，给出一些建图的方式，，但是，和以往不同的是，以前的边的关系给的都是点与点间的关系，，这种题给的方式是区间，，比如说 u->[l, r] 表示的就是u和这个区间的所有点间都有一条边，，因为一个点也可以看成一个只有自己的区间，，所以我们可以将这类关系统一看成 \([l_1, r_1]->[l_2, r_2]\) ，，

容易想到的方法就是直接两个 for 上去，，建出每一条边，，数据很小的时候没问题，，，但是当n 很大时，，显然建图的复杂度可能就是 \(O(n^2m)\) 这样不管求最短路就炸了，，，

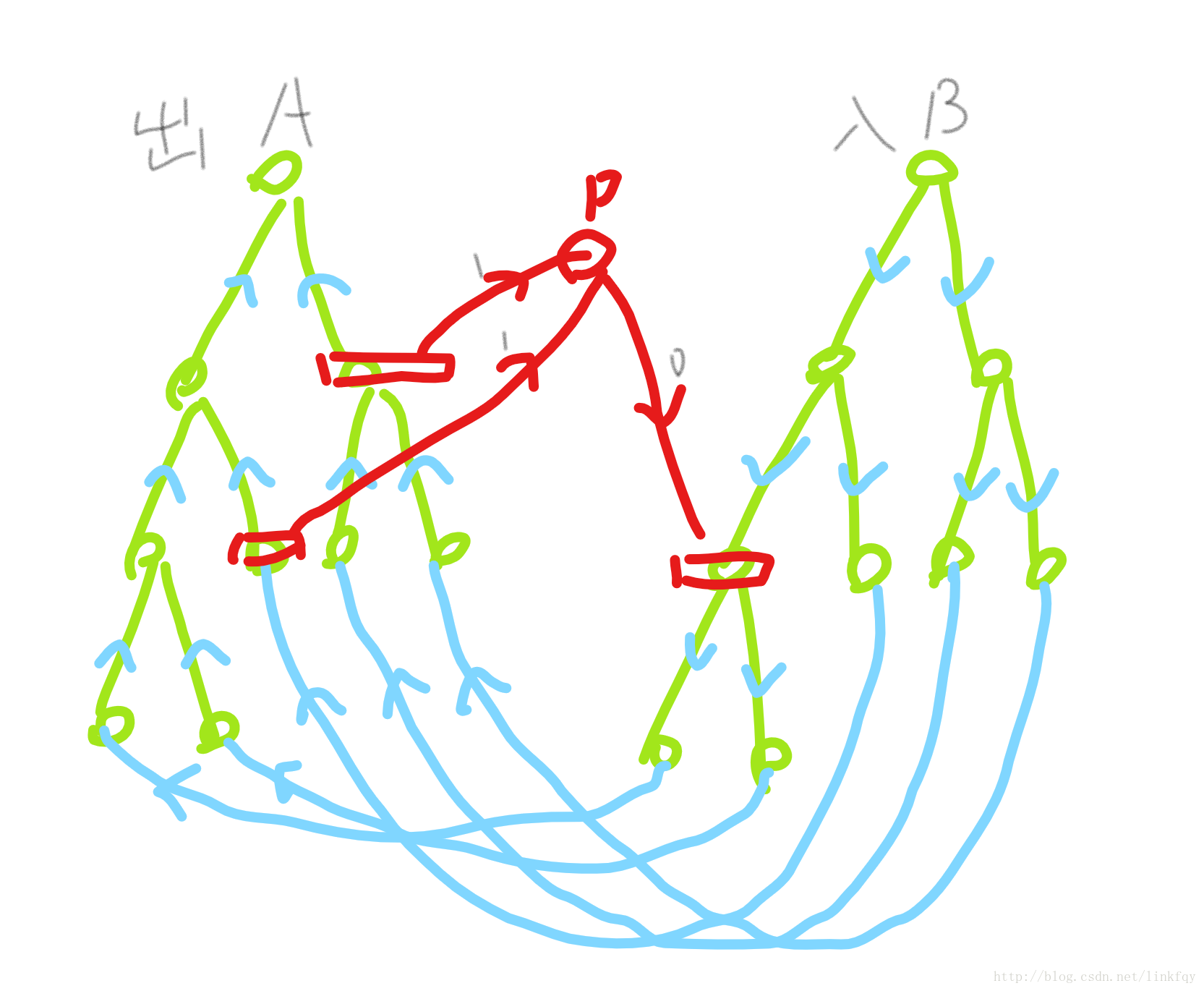
一种优化的方法是我们在这两个区间之间加一个点，，这样前面的区间（成为出区间）和后面的一个区间（称为入区间）都和这个点 \(p\) 连，，也就是 \(\forall u \in [l_1, r_1]: addedge(u, p, w)\) 而 \(\forall v \in [l_2, r_2]: addedge(p, v, 0)\) （ \([l_1, r_1]-_u>p-_0>[l_2, r_2]\) ）这样子就可以降一维的建图，，复杂度就是 \(O(2nm)\) ，，但是这样还是很高，，

这时的建图是线性的建图方式，，线性+区间==线段树？？！！，，这是我做这道题学习到的最有价值的一个处理方式，，在降了一维之后，虽然是线性的建图，，但是点还是很多，，而线段树恰好可以用很少的子区间来表示原来的区间，，，如果将线段树中的每一个表示的区间看成一个点，，那么我们就可以用很少的点来建图，，，这样就可以将上面的n次的建图降下去，，，

那么这时的问题就变成了该如何利用线段树来处理，，

我们需要两棵线段树，，一棵看成入树另一棵看成出树，，

首先我们的目的是用少量的区间来表示原来的很大的区间，以达到用很少的点来表示原来的所有点，，优化的问题用线段树解决了，，但是，如何正确的表示原来的所有点呢，，，

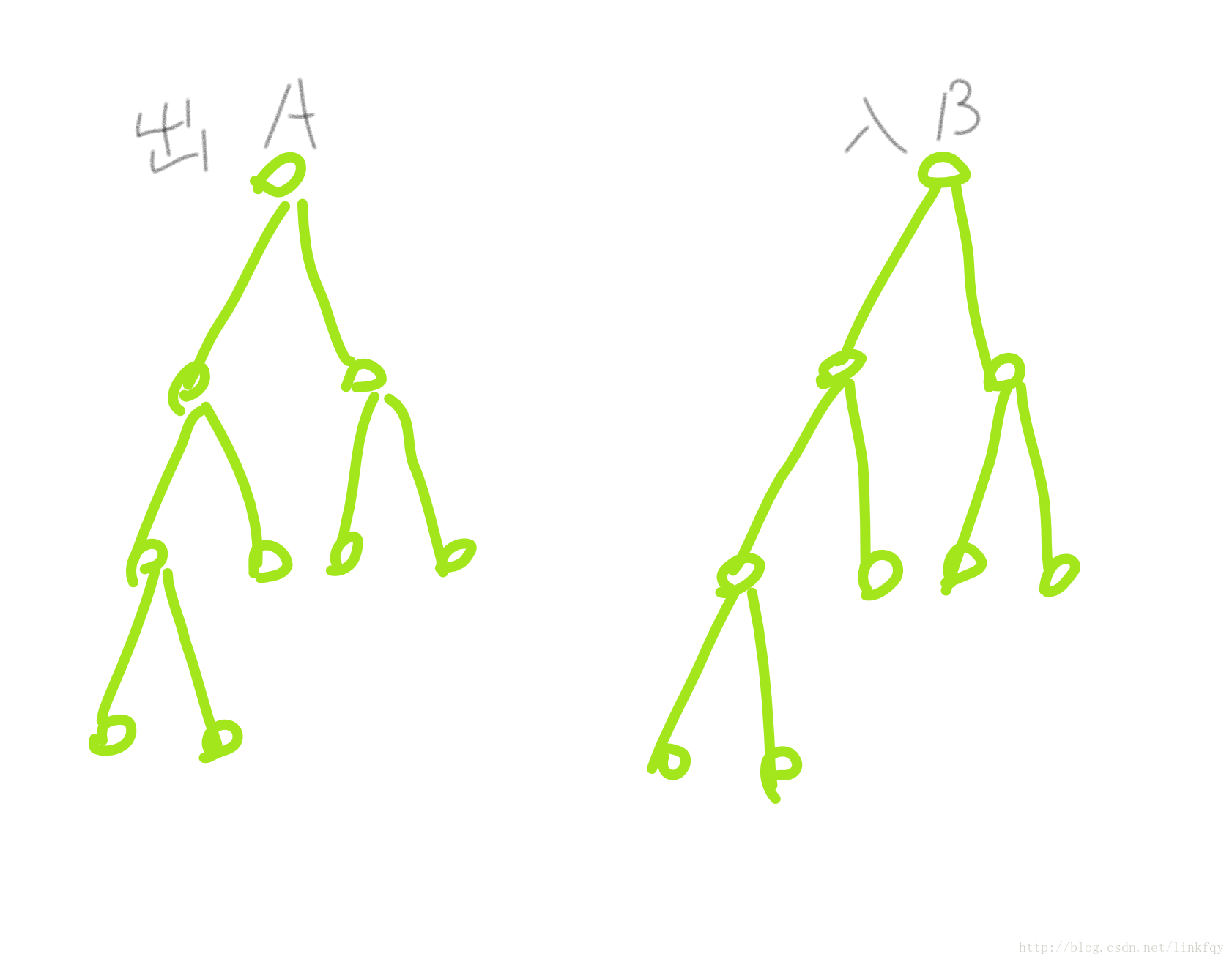
线段树的每一个节点表示一个区间，，这个节点可以表示他下面的所有点，，也就是说，，我们可以从上向下的看，，定义选择了一个节点，，就选择了下面的所有点，，，按照这个思想，入树中的一个节点要向其儿子连一条指向儿子的有向边，，也就是说，，入树中所有的边指向下，，用 down 表示

同理，，对于出树，，我们要保证在一个节点要能表示所有的点，，于是就是一个节点下的所有节点都要指向它，，，这样看这棵树就是一个向上的树，，用 up 表示，，

这个样子的：

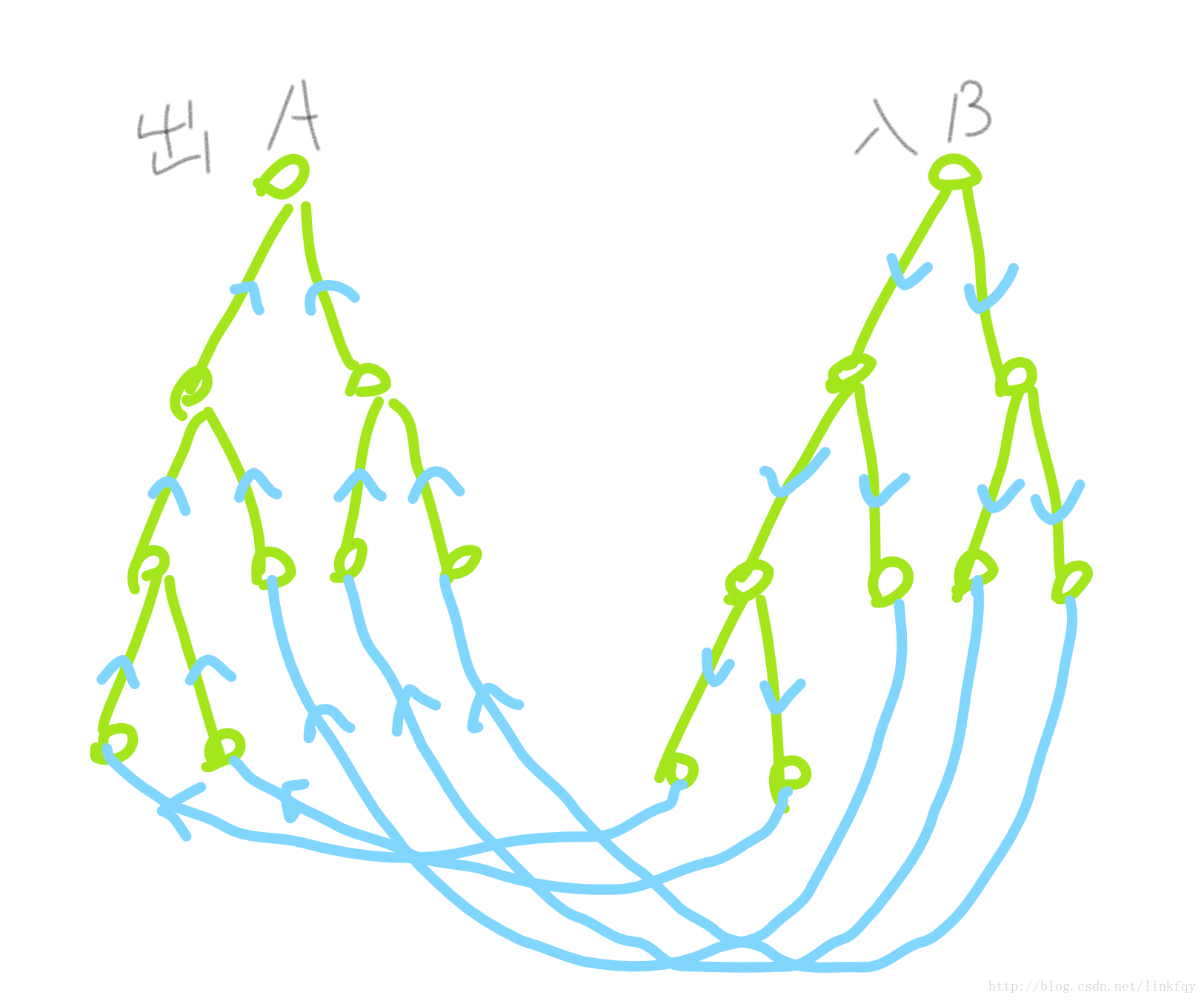
这样最后在这样初始图加上题目给的一些条件的边跑一边最短路就可以了，，

加上题目的边后的图大致是这样的：

实际上，，这里的线段树的作用只是一个建树和查询其子区间的作用，，这个思想有点像是分块，，，只要能找到一个合理的区间分块，，用一些合理的、数量少的区间表示原来的区间，，就能达到减少点数的作用，，，，而线段树恰好是一个熟悉的、好操作的区间划分模型，，所以很多人都对于区间图的最短路问题都是套一个线段树的板子，，

回到这道题，，题目的加边方式只有点对区间和区间对点两种，，所以我们可以先预留出那n个点，，可以想象成放在这两棵树之间的一排点（不用再将两棵树的叶子节点相连，，），，，

然后再处理出出树、入树的边后，，对于 u->[l, r] 和 u->v 的边，，从点 u 向入树的符合条件的节点连边即可，，因为之前说的入树保证了每一个节点是可以到其下面的叶子节点的，，所以我们这样连边就相当于是点 u 向区间的每一个点连边，，，

同理对于 [l, r]->u 这样的边，，我们将入树的对应的节点和点 u 相连，，这样就保证入树中这个区间下的叶子节点可以通过这些区间到点 u ，，这样也满足了题意的同时减少的连边的复杂度，，，

最后跑最短路，，前n个点的 dis[i] 即为源图的那些点的最短路，，，

于是我们通过加点减边的方式减小了建图的时间复杂度，，

关于处理出树、入树的操作，，也就是线段树的建树过程，，其实线段树并不维护任何信息，，我们只是用它自己每个节点表示一个区间这个自身的性质，，所以为了建图，，，我们需要对每一个节点连一些边，，，也就是用一个 id[rt] 标记一下每一个节点的标号即可，，，

最后的代码：

#include <bits/stdc++.h>

#define aaa cout<<233<<endl;

#define endl '\n'

using namespace std;

typedef long long ll;

typedef unsigned long long ull;

typedef long double ld;

// mt19937 rnd(time(0));

const int inf = 0x3f3f3f3f;//1061109567 > 1e9

const ll linf = 0x3f3f3f3f3f3f3f3f;

const double eps = 1e-6;

const double pi = 3.14159265358979;

const int maxn = 1e6 + 5;

const int maxm = 1e7 + 233;

const int mod = 1e9 + 7;

struct Dijkstra

{

    struct edge

    {

        int to, nxt; ll w;

    }edge[maxm];

    int tot, head[maxm];

    void init()

    {

        tot = 0;

        memset(head, -1, sizeof head);

    }

    void addedge(int u, int v, ll w)

    {

        edge[tot].to = v;

        edge[tot].w = w;

        edge[tot].nxt = head[u];

        head[u] = tot++;

    }

    struct node

    {

        int v; ll w;

        node(){}

        node(int _v, ll _w):v(_v), w(_w){}

        const bool operator<(const node &r)const

        {

            return w > r.w;

        }

    };

    bool vis[maxn];

    ll dis[maxn];

    priority_queue<node> pq;

    void dijkstra(int s, int n)

    {

        memset(vis, false, sizeof vis);

        memset(dis, inf, sizeof dis);

        while(!pq.empty())pq.pop();

        pq.push(node(s, 0));

        dis[s] = 0;

        node t;

        int u;

        while(!pq.empty())

        {

            t = pq.top(); pq.pop();

            u = t.v;

            if(vis[u])continue;

            vis[u] = true;

            for(int i = head[u]; ~i; i = edge[i].nxt)

            {

                int v = edge[i].to;

                ll w = edge[i].w;

                if(dis[v] > t.w + w)

                {

                    dis[v] = t.w + w;

                    pq.push(node(v, dis[v]));

                }

            }

        }

    }

    void print(int n)

    {

        for(int i = 1; i <= n; ++i)cout << (dis[i] == linf ? -1 : dis[i]) << " ";cout << endl;

    }

}dijkstra;

int cnt;

struct segmentTree

{

    int id[maxn];           // 节点标记数组，，记录线段树中每一个节点的标号，，从 n+1 开始，，前面的n个是原来的点

    void build(int rt, int l, int r, bool flag)     // 建树（建图，，flag == false 表示是一棵入树，边向下，节点指向儿子

    {

        id[rt] = ++cnt;

        if(l == r)

        {

            int u = id[rt];

            int v = l;

            if(flag)swap(u, v);

            dijkstra.addedge(u, v, 0);

            return;

        }

        int mid = l + r >> 1;

        build(rt << 1, l, mid, flag);

        build(rt << 1 | 1, mid + 1, r, flag);

        // pushup

        int u = id[rt];

        int v = id[rt << 1];

        if(flag)swap(u, v);

        dijkstra.addedge(u, v, 0);

        u = id[rt];

        v = id[rt << 1 | 1];

        if(flag)swap(u, v);

        dijkstra.addedge(u, v, 0);

        return;

    }

    void addedge(int rt, int l, int r, int U, int L, int R, ll w, bool flag)    // flag == false 表示 u->[l, r] ，，

    {

        if(l > R || L > r)return;

        if(L <= l && r <= R)

        {

            int u = U;

            int v = id[rt];

            if(flag)swap(u, v);

            dijkstra.addedge(u, v, w);

            return;

        }

        int mid = l + r >> 1;

        if(L <= mid)addedge(rt << 1, l, mid, U, L, R, w, flag);

        if(R >  mid)addedge(rt << 1 | 1, mid + 1, r, U, L, R, w, flag);

        return;

    }

}down, up;

int main()

{

    // double pp = clock();

    // freopen("233.in", "r", stdin);

    // freopen("233.out", "w", stdout);

    ios_base::sync_with_stdio(0);

    cin.tie(0);cout.tie(0);

    int n, q, s;

    cin >> n >> q >> s;

    cnt = n;                // 出树、入树等的辅助点的标记从n+1开始

    dijkstra.init();

    down.build(1, 1, n, false);

    up.build(1, 1, n, true);

    int t, u, v, w, l, r;

    while(q--)

    {

        cin >> t;

        if(t == 1)

        {

            cin >> u >> v >> w;

            l = r = v;

            t = 2;

        }

        else

            cin >> u >> l >> r >> w;

        if(t == 2)

            down.addedge(1, 1, n, u, l, r, w, false);   // u -> [l, r]

        else

            up.addedge(1, 1, n, u, l, r, w, true);      // [l, r] -> u

    }

    dijkstra.dijkstra(s, cnt);

    dijkstra.print(n);

    // cout << endl << (clock() - pp) / CLOCKS_PER_SEC << endl;

    return 0;

}

以上的一些内容和图片参考这个dalao的博客

最后的AC代码的大致思路是参考葫芦爷大佬的板子

hdu-5361In Touch

差不多的题，，貌似解法有很多，，如果用这种方法来解的话，，只用一棵入树就行了，，，还有可能得改一改写的姿势，，，（重载w爆int一晚上没看出来的怕不是只有我一个了吧，，，emmmm

AC_1

#include <bits/stdc++.h>

// #include <iostream>

// #include <queue>

// #include <cstring>

#define aaa cout<<233<<endl;

#define endl '\n'

using namespace std;

typedef long long ll;

typedef unsigned long long ull;

typedef long double ld;

// mt19937 rnd(time(0));

const int inf = 0x3f3f3f3f;//1061109567 > 1e9

const ll linf = 0x3f3f3f3f3f3f3f3f;

const double eps = 1e-6;

const double pi = 3.14159265358979;

const int maxn = 2e5 + 5;

const int maxm = 1e7 + 233;

const int mod = 1e9 + 7;

inline int read()   //快读

{

    int ans=0;

    char ch=getchar();

    while(!isdigit(ch))

        ch=getchar();

    while(isdigit(ch))

        ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();

    return ans;

}

int n;

struct edge

{

    int to, nxt;

    ll w;

}edge[maxm];

int tot, head[maxn << 3];

void init(int n)

{

    tot = 0;

    for(int i = 0; i <= n; ++i)head[i] = -1;

}

void ADDEDGE(int u, int v, ll w)

{

    edge[tot].to = v;

    edge[tot].w = w;

    edge[tot].nxt = head[u];

    head[u] = tot++;

}

struct node

{

    int v;

    ll w;

    node(){};

    node(int _v, ll _w): v(_v), w(_w){};

    const bool operator<(const node &r)const{

        return w > r.w;

    }

}tmp;

bool vis[maxn << 3];

ll dis[maxn << 3];

priority_queue<node> pq;

void dijkstra(int s, int n)

{

    for(int i = 0; i <= n; ++i)dis[i] = linf;

    for(int i = 0; i <= n; ++i)vis[i] = false;

    while(!pq.empty())pq.pop();

    pq.push(node(s, 0));

    dis[s] = 0;

    while(!pq.empty())

    {

        tmp = pq.top(); pq.pop();

        if(vis[tmp.v])continue;

        vis[tmp.v] = true;

        for(int i = head[tmp.v]; ~i; i = edge[i].nxt)

        {

            int v = edge[i].to;

            if(dis[v] > dis[tmp.v] + edge[i].w)

            {

                dis[v] = dis[tmp.v] + edge[i].w;

                pq.push(node(v, dis[v]));

            }

        }

    }

}

int cnt;

void build(int rt, int l, int r)

{

    if(l == r)

    {

        cnt = max(cnt, rt + n);

        ADDEDGE(rt + n, l, 0);

        return;

    }

    int mid = l + r >> 1;

    build(rt << 1, l, mid);

    build(rt << 1 | 1, mid + 1, r);

    ADDEDGE(rt + n, (rt << 1) + n, 0);

    ADDEDGE(rt + n, (rt << 1 | 1) + n, 0);

}

int L, R, W, U;

void addedge(int rt, int l, int r)

{

    if(L > r || l > R)return;

    if(L <= l && r <= R)

    {

        ADDEDGE(U, rt + n, W);

        return;

    }

    int mid = l + r >> 1;

    if(L <= mid)addedge(rt << 1, l, mid);

    if(R >  mid)addedge(rt << 1 | 1, mid + 1, r);

}

int l[maxn], r[maxn], c[maxn];

int main()

{

    // double pp = clock();

    // freopen("233.in", "r", stdin);

    // freopen("233.out", "w", stdout);

    // ios_base::sync_with_stdio(0);

    // cin.tie(0);cout.tie(0);

    // int t; cin >> t;

    // int t; scanf("%d", &t);

    int t; t = read();

    while(t--)

    {

        // cin >> n;

        scanf("%d", &n);

        for(int i = 1; i <= n; ++i)l[i] = read();

        for(int i = 1; i <= n; ++i)r[i] = read();

        for(int i = 1; i <= n; ++i)c[i] = read();

        init(n << 3);

        cnt = 0;

        build(1, 1, n);

        for(int i = 1; i <= n; ++i)

        {

            U = i;

            L = i + l[i]; R = i + r[i]; W = c[i];

            addedge(1, 1, n);

            L = i - r[i]; R = i - l[i];

            addedge(1, 1, n);

        }

        dijkstra(1, cnt);

        printf("0");

        for(int i = 2; i <= n; ++i)

            printf(" %lld", (dis[i] == linf ? -1 : dis[i]));

        puts("");

    }

    // cout << endl << (clock() - pp) / CLOCKS_PER_SEC << endl;

    return 0;

}

AC_2

（不加快读也没事，，，就是不能memset，，，卡memset好恶心，，，，

#include <bits/stdc++.h>

#define aaa cout<<233<<endl;

#define endl '\n'

using namespace std;

typedef long long ll;

typedef unsigned long long ull;

typedef long double ld;

// mt19937 rnd(time(0));

const int inf = 0x3f3f3f3f;//1061109567 > 1e9

const ll linf = 0x3f3f3f3f3f3f3f3f;

const double eps = 1e-6;

const double pi = 3.14159265358979;

const int maxn = 2e5 + 5;

const int maxm = 1e7 + 233;

const int mod = 1e9 + 7;

inline int read()   //快读

{

    int ans=0;

    char ch=getchar();

    while(!isdigit(ch))

        ch=getchar();

    while(isdigit(ch))

        ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();

    return ans;

}

struct Dijkstra

{

    struct edge

    {

        int to, nxt;

        ll w;

    }edge[maxm];

    int tot, head[maxn << 3];

    void init(int n)

    {

        tot = 0;

        // memset(head, -1, sizeof head);

        for(int i = 0; i <= n; ++i)head[i] = -1;

    }

    void addedge(int u, int v, ll w)

    {

        edge[tot].to = v;

        edge[tot].w = w;

        edge[tot].nxt = head[u];

        head[u] = tot++;

    }

    struct node

    {

        int v; ll w;

        node(){}

        node(int _v, ll _w):v(_v), w(_w){}

        const bool operator<(const node &r)const

        {

            return w > r.w;

        }

    };

    bool vis[maxn << 3];

    ll dis[maxn << 3];

    priority_queue<node> pq;

    void dijkstra(int s, int n)

    {

        // memset(vis, false, sizeof vis);

        // memset(dis, inf, sizeof dis);

        for(int i = 0; i <= n; ++i)vis[i] = false;

        for(int i = 0; i <= n; ++i)dis[i] = linf;

        while(!pq.empty())pq.pop();

        pq.push(node(s, 0));

        dis[s] = 0;

        node t; int u;

        while(!pq.empty())

        {

            t = pq.top(); pq.pop();

            u = t.v;

            if(vis[u])continue;

            vis[u] = true;

            for(int i = head[u]; ~i; i = edge[i].nxt)

            {

                int v = edge[i].to;

                ll w = edge[i].w;

                if(dis[v] > t.w + w)

                {

                    dis[v] = t.w + w;

                    pq.push(node(v, dis[v]));

                }

            }

        }

    }

    void print(int n)

    {

        printf("0");

        for(int i = 2; i <= n; ++i)printf(" %lld", (dis[i] == linf ? -1 : dis[i]));

        puts("");

    }

}dijkstra;

int cnt;

struct segmentTree

{

    int id[maxn << 3];

    void build(int rt, int l, int r, bool flag)

    {

        id[rt] = ++cnt;

        if(l == r)

        {

            int u = id[rt];

            int v = l;

            if(flag)swap(u, v);

            dijkstra.addedge(u, v, 0);

            return;

        }

        int mid = l + r >> 1;

        build(rt << 1, l, mid, flag);

        build(rt << 1 | 1, mid + 1, r, flag);

        int u = id[rt];

        int v = id[rt << 1];

        if(flag)swap(u, v);

        dijkstra.addedge(u, v, 0);

        u = id[rt];

        v = id[rt << 1 | 1];

        if(flag)swap(u, v);

        dijkstra.addedge(u, v, 0);

        return;

    }

    void addedge(int rt, int l, int r, int U, int L, int R, ll w, bool flag)

    {

        if(L > r || R < l)return;

        if(L <= l && r <= R)

        {

            int u = U;

            int v = id[rt];

            if(flag)swap(u, v);

            dijkstra.addedge(u, v, w);

            return;

        }

        int mid = l + r >> 1;

        if(L <= mid)addedge(rt << 1, l, mid, U, L, R, w, flag);

        if(R >  mid)addedge(rt << 1 | 1, mid + 1, r, U, L, R, w, flag);

        return;

    }

}down; //, up;

int l[maxn], r[maxn], c[maxn];

int main()

{

    // double pp = clock();

    // freopen("233.in", "r", stdin);

    // freopen("233.out", "w", stdout);

    // ios_base::sync_with_stdio(0);

    // cin.tie(0);cout.tie(0);

    int t; t = read();

    while(t--)

    {

        int n; n = read();

        for(int i = 1; i <= n; ++i)l[i] = read();

        for(int i = 1; i <= n; ++i)r[i] = read();

        for(int i = 1; i <= n; ++i)c[i] = read();

        cnt = n;

        dijkstra.init(n << 3);

        down.build(1, 1, n, false);

        // up.build(1, 1, n, true);

        for(int i = 1; i <= n; ++i)

        {

            down.addedge(1, 1, n, i, l[i] + i, r[i] + i, c[i], false);

            down.addedge(1, 1, n, i, max(1, i - r[i]), max(1, i - l[i]), c[i], false);

        }

        dijkstra.dijkstra(1, cnt);

        dijkstra.print(n);

    }

    // cout << endl << (clock() - pp) / CLOCKS_PER_SEC << endl;

    return 0;

}

(end)

cf-786B区间图最短路的更多相关文章

CF Destroying Roads (最短路)
Destroying Roads time limit per test 2 seconds memory limit per test 256 megabytes input standard in ...
CF 241E flights 最短路,重复迭代直到稳定难度:3
http://codeforces.com/problemset/problem/241/E 首先检测哪些点会出现在从起点到终点的路上,可以用dfs或者迭代, 然后,对于所有的边,设f为边起点,t为边 ...
hdoj 1385Minimum Transport Cost
卧槽....最近刷的cf上有最短路,本来想拿这题复习一下.... 题意就是在输出最短路的情况下,经过每个节点会增加税收,另外要字典序输出,注意a到b和b到a的权值不同然后就是处理字典序的问题,当松弛 ...
CF786B/CF787D Legacy
题目描述: luogu cf cf 题解: 最短路+线段树优化建图. 考虑本题的边是点->点.段->点和点->段,我们可以建线段树然后拆成入点和出点. 入点:儿子->父亲,边权 ...
CF 787D Legacy（线段树思想构图+最短路）
D. Legacy time limit per test 2 seconds memory limit per test 256 megabytes input standard input out ...
Codeforces.786B.Legacy(线段树优化建图最短路Dijkstra)
题目链接 \(Description\) 有\(n\)个点.你有\(Q\)种项目可以选择(边都是有向边,每次给定\(t,u,v/lr,w\)): t==1,建一条\(u\to v\)的边,花费\(w\ ...
CodeForces 786B Legacy（线段树优化建图+最短路）
[题目链接] http://codeforces.com/problemset/problem/786/B [题目大意] 给出一些星球,现在有一些传送枪,可以从一个星球到另一个星球, 从一个星球到另一 ...
cf 843 D Dynamic Shortest Path [最短路+bfs]
题面: 传送门思路: 真·动态最短路但是因为每次只加1 所以可以每一次修改操作的时候使用距离分层的bfs,在O(n)的时间内解决修改这里要用到一个小技巧: 把每条边(u,v)的边权表示为dis[ ...
CF 672C 两个人捡瓶子最短路与次短路思想
C. Recycling Bottles time limit per test 2 seconds memory limit per test 256 megabytes input standar ...

随机推荐

Docker 更改容器映射端口
1.编辑容器的配置文件进行更改端口: docker run 运行启动时 -p 可以指定容器启动映射端口 ( ) 可以编辑配置文件进行修改:(需要重启docker 服务不止是是容器才能生效.只能重 ...
kafka消费端提交offset的方式
Kafka 提供了 3 种提交 offset 的方式自动提交复制 1234 consumer.commitSync(); 手动异步提交 offset 复制 1 consumer.commitAsy ...
STL next_permutation 全排列
调用方法: ]={,,,}; )){ ;i<;i++) printf("%d ",arr[i]); puts(""); } 测试效果: 注:可以看到1 2 ...
LOJ3097 SNOI2019 通信题解
题目链接费用流,当建边需要依靠位置和权值两个偏序关系时,可以用cdq分治优化建边. 代码: #include<bits/stdc++.h> using namespace std; #d ...
[linux][c/c++]代码片段02
gcc `pkg-config --cflags gtk+-3.0` -o example-1 example-1.c `pkg-config --libs gtk+-3.0` #include &l ...
mybatis 根据多个id查询数据 foreach标签
//根据设备多个id获取设备信息 public List<Devices> getDevicesAll(@Param("devicesIds") String[] de ...
MYSQL避免重复插入记录的三种方法
方案一:使用ignore关键字如果是用主键primary或者唯一索引unique区分了记录的唯一性,避免重复插入记录可以使用: insert ignore into table_name(ema ...
浅谈 HTTP协议
1.什么是http协议Hyper Text Transport Portocal(超文本传输协议)HTTP协议是应用层协议浏览器和web服务器通讯时遵守的约定互联网使用最多的协议提供超文本的传输服务通 ...
Net core学习系列（九）——Net Core配置
一.简介 NET Core为我们提供了一套用于配置的API,它为程序提供了运行时从文件.命令行参数.环境变量等读取配置的方法.配置都是键值对的形式,并且支持嵌套,.NET Core还内建了从配置反序列 ...
聊聊Dubbo（六）：核心源码-Filter链原理
转载:https://www.jianshu.com/p/6dd76ce7338f 0 前言对于Java WEB应用来说,Spring的Filter可以拦截WEB接口调用,但对于Dubbo接口,Sp ...

cf-786B区间图最短路