#2590. 「NOIP2009」最优贸易

C 国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 1 条。

C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 C 国 nnn 个城市的标号从 1∼n，阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 n 个城市。

阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 C 国有 5 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

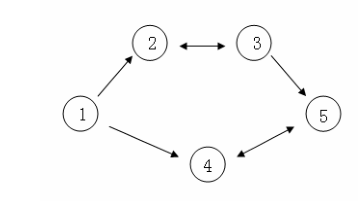
现在给出 n个城市的水晶球价格， m 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

分析：

说说我本来的思路，我想用spfa法遍历，一边遍历一边找出到第i个顶点时的最大值和最小值，并保存下来，至于双向边还是单向边，我用一个计数器来记录当前是第几次到达i点，如果是0，就可以扩展它，如果大于0，就不能（显然这一个方法不对......）

最后就用maxs[i]-mins[i]找到ans；提交，10分。

后来学到了另一种思路：跑两遍spfa。

正向跑一遍记录min[i]，反向再跑一遍记录max[i]，这样不仅能保证连通性（即当前点一定能到终点），也能比较得ans；

#include<bits/stdc++.h>
#define inf 1e9;
using namespace std;
int n,m,a[],ans=,minn[],maxx[]={};
struct node{
    int to,next,wei;
}e[];
void read(int &x)
{
    x=;int f=;char s=getchar();
    while(s>''||s<''){if(s=='-')f=-;s=getchar();}
    while(s<=''&&s>=''){x=x*+s-'';s=getchar();}
    x*=f;
}
void print(int x)
{
    if(x<){putchar('-');x=-x;}
    if(x>){print(x/);}
    putchar(x%+'');
}
int head[][],tot=,vis[];
void add(int x,int y){
    tot++;
    e[tot].to=y;
    e[tot].next=head[x][];
    head[x][]=tot;
    tot++;
    e[tot].to=x;
    e[tot].next=head[y][];
    head[y][]=tot;
}
queue<int> q;
void spfa(int start)
{
    memset(vis,,sizeof vis);
    memset(minn,0x3f3f3f3f,sizeof minn);
    vis[start]=;
    q.push(start);
    minn[start]=a[start];
    while(!q.empty())
    {
        int u=q.front();q.pop();
        vis[u]=;
        for(int p=head[u][];p!=-;p=e[p].next)
        {
            int v=e[p].to;
            if(minn[v]>min(a[v],minn[u]))
            {
                minn[v]=min(a[v],minn[u]);
                if(!vis[v])
                {
                    q.push(v),vis[v]=;
                }
            }

        }
    }
}
void spfa2(int start)
{
    memset(vis,,sizeof vis);
    vis[start]=;
    q.push(start);
    maxx[start]=a[start];
    ans=max(ans,maxx[n]-minn[n]);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        vis[u]=;
        for(int p=head[u][];p!=-;p=e[p].next)
        {
            int v=e[p].to;
            if(maxx[v]<max(maxx[u],a[v]))
            {
                maxx[v]=max(a[v],maxx[u]);
                ans=max(maxx[v]-minn[v],ans);
                if(!vis[v]){
                    q.push(v),vis[v]=;
                }
            }

        }
    }
}
int main()
{
    read(n),read(m);
    memset(head,-,sizeof head);
    for(int i=;i<=n;i++)
    {
        read(a[i]);
    }
    for(int i=;i<=m;i++){
        int x,y,z;
        read(x),read(y),read(z);
        add(x,y);
        if(z==) add(y,x);
    }
    spfa();
    spfa2(n);
    print(ans);
    return ;
}