Andrew Ng机器学习 三：Multi-class Classification and Neural Networks

背景：识别手写数字，给一组数据集ex3data1.mat，，每个样例都为灰度化为20*20像素，也就是每个样例的维度为400，加载这组数据后，我们会有5000*400的矩阵X(5000个样例)，会有5000*1的矩阵y(表示每个样例所代表的数据)。现在让你拟合出一个模型，使得这个模型能很好的预测其它手写的数字。

（注意：我们用10代表0(矩阵y也是这样)，因为Octave的矩阵没有0行）

我们随机可视化100个样例，可以看到如下图所示：

一：多类别分类(Multi-class Classification)

　　在这我们使用逻辑回归多类别分类去拟合数据。在这组数据，总共有10类别，我们可以将它们分成10个2元分类问题，最后我们选择一个让$h_\theta^i(x)$最大的$i$。

　　逻辑回归脚本ex3.m：

%% Machine Learning Online Class - Exercise  | Part : One-vs-all

%  Instructions
%  ------------
%
%  This file contains code that helps you get started on the
%  linear exercise. You will need to complete the following functions
%  in this exericse:
%
%     lrCostFunction.m (logistic regression cost function)
%     oneVsAll.m
%     predictOneVsAll.m
%     predict.m
%
%  For this exercise, you will not need to change any code in this file,
%  or any other files other than those mentioned above.
%

%% Initialization
clear ; close all; clc

%% Setup the parameters you will use for this part of the exercise
input_layer_size  = ;  % 20x20 Input Images of Digits
num_labels = ;          %  labels, from  to
                          % (note that we have mapped "" to label )

%% =========== Part : Loading and Visualizing Data =============
%  We start the exercise by first loading and visualizing the dataset.
%  You will be working with a dataset that contains handwritten digits.
%

% Load Training Data
fprintf('Loading and Visualizing Data ...\n')

load('ex3data1.mat'); % training data stored in arrays X, y
m = size(X, );

% Randomly select  data points to display
rand_indices = randperm(m);
sel = X(rand_indices(:), :);

displayData(sel);

fprintf('Program paused. Press enter to continue.\n');
pause;

%% ============ Part 2a: Vectorize Logistic Regression ============
%  In this part of the exercise, you will reuse your logistic regression
%  code from the last exercise. You task here is to make sure that your
%  regularized logistic regression implementation is vectorized. After
%  that, you will implement one-vs-all classification for the handwritten
%  digit dataset.
%

% Test case for lrCostFunction
fprintf('\nTesting lrCostFunction() with regularization');

theta_t = [-; -; ; ];
X_t = [ones(,) reshape(:,,)/];
y_t = ([;;;;] >= 0.5);
lambda_t = ;
[J grad] = lrCostFunction(theta_t, X_t, y_t, lambda_t);

fprintf('\nCost: %f\n', J);
fprintf('Expected cost: 2.534819\n');
fprintf('Gradients:\n');
fprintf(' %f \n', grad);
fprintf('Expected gradients:\n');
fprintf(' 0.146561\n -0.548558\n 0.724722\n 1.398003\n');

fprintf('Program paused. Press enter to continue.\n');
pause;
%% ============ Part 2b: One-vs-All Training ============
fprintf('\nTraining One-vs-All Logistic Regression...\n')

lambda = 0.1;
[all_theta] = oneVsAll(X, y, num_labels, lambda); %*，每行表示标签i的拟合参数

fprintf('Program paused. Press enter to continue.\n');
pause;

%% ================ Part : Predict for One-Vs-All ================

pred = predictOneVsAll(all_theta, X);

fprintf('\nTraining Set Accuracy: %f\n', mean(double(pred == y)) * );

ex3.m

　　1，正则化逻辑回归代价函数(忽略偏差项$\theta_0$的正则化)：

　　$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]+\frac{\lambda }{2m}\sum_{j=1}^{n}\theta_j^{2}$

　　

　　2，梯度下降：

　　不带学习速率(给之后fmincg作为梯度下降使用)：

　　　　$\frac{\partial J(\theta)}{\partial \theta_0}=\frac{1}{m}\sum_{i=1}^{m}[(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_0]$  for $j=0$

　　　　$\frac{\partial J(\theta)}{\partial \theta_j}=(\frac{1}{m}\sum_{i=1}^{m}[(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j])+\frac{\lambda }{m}\theta_j $ for $j\geq 1$

　　

　　代价函数代码：

function [J, grad] = lrCostFunction(theta, X, y, lambda)
%LRCOSTFUNCTION Compute cost and gradient for logistic regression with
%regularization
%   J = LRCOSTFUNCTION(theta, X, y, lambda) computes the cost of using
%   theta as the parameter for regularized logistic regression and the
%   gradient of the cost w.r.t. to the parameters. 

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly
J = ;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta
%
% Hint: The computation of the cost function and gradients can be
%       efficiently vectorized. For example, consider the computation
%
%           sigmoid(X * theta)
%
%       Each row of the resulting matrix will contain the value of the
%       prediction for that example. You can make use of this to vectorize
%       the cost function and gradient computations.
%
% Hint: When computing the gradient of the regularized cost function,
%       there're many possible vectorized solutions, but one solution
%       looks like:
%           grad = (unregularized gradient for logistic regression)
%           temp = theta;
%           temp() = ;   % because we don't add anything for j = 0
%           grad = grad + YOUR_CODE_HERE (using the temp variable)
%
    h=sigmoid(X*theta);
    theta(,)=;
    J=(-(y')*log(h)-(1-y)'*log(-h))/m+lambda//m*sum(power(theta,));%代价函数
    grad=(X'*(h-y))./m+(lambda/m).*theta; %不带学习速率的梯度下降

% =============================================================

grad = grad(:);

end

lrCostFunction.m

　　拟合参数：

function [all_theta] = oneVsAll(X, y, num_labels, lambda)
%ONEVSALL trains multiple logistic regression classifiers and returns all
%the classifiers in a matrix all_theta, where the i-th row of all_theta
%corresponds to the classifier for label i
%   [all_theta] = ONEVSALL(X, y, num_labels, lambda) trains num_labels
%   logistic regression classifiers and returns each of these classifiers
%   in a matrix all_theta, where the i-th row of all_theta corresponds
%   to the classifier for label i

% Some useful variables
m = size(X, ); %
n = size(X, ); %

% You need to return the following variables correctly
all_theta = zeros(num_labels, n + ); %*

% Add ones to the X data matrix
X = [ones(m, ) X]; %*

% ====================== YOUR CODE HERE ======================
% Instructions: You should complete the following code to train num_labels
%               logistic regression classifiers with regularization
%               parameter lambda.
%
% Hint: theta(:) will return a column vector.
%
% Hint: You can use y == c to obtain a vector of 's and 0's that tell you
%       whether the ground truth is true/false for this class.
%
% Note: For this assignment, we recommend using fmincg to optimize the cost
%       function. It is okay to use a for-loop (for c = :num_labels) to
%       loop over the different classes.
%
%       fmincg works similarly to fminunc, but is more efficient when we
%       are dealing with large number of parameters.
%
% Example Code for fmincg:
%
%     % Set Initial theta
%     initial_theta = zeros(n + , );
%
%     % Set options for fminunc
%     options = optimset('GradObj', 'on', 'MaxIter', );
%
%     % Run fmincg to obtain the optimal theta
%     % This function will return theta and the cost
%     [theta] = ...
%         fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), ...
%                 initial_theta, options);
%

for c=:num_labels,
    initial_theta = zeros(n + , ); %*
    options = optimset('GradObj', 'on', 'MaxIter', );
    [theta] = ...
             fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), ...
                 initial_theta, options);
    all_theta(c,:)=theta; %给标签c拟合参数
end;

% =========================================================================

end

oneVsAll.m

　　3， 预测：我们根据我们拟合好的参数$\theta$去预测样例。我们可以看到我们使用逻辑回归去拟合对类别分类问题的准确率为95%。我们可以增加更多的特征，让我们的准确率更高，但因为过高的维度，最后我们可能要花费昂贵的训练代价。

function p = predictOneVsAll(all_theta, X)
%PREDICT Predict the label for a trained one-vs-all classifier. The labels
%are in the range ..K, where K = size(all_theta, ).
%  p = PREDICTONEVSALL(all_theta, X) will return a vector of predictions
%  for each example in the matrix X. Note that X contains the examples in
%  rows. all_theta is a matrix where the i-th row is a trained logistic
%  regression theta vector for the i-th class. You should set p to a vector
%  of values from ..K (e.g., p = [; ; ; ] predicts classes , , ,
%  for  examples) 

m = size(X, );
num_labels = size(all_theta, );

% You need to return the following variables correctly
p = zeros(size(X, ), );

% Add ones to the X data matrix
X = [ones(m, ) X];

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned logistic regression parameters (one-vs-all).
%               You should set p to a vector of predictions (from  to
%               num_labels).
%
% Hint: This code can be done all vectorized using the max function.
%       In particular, the max function can also return the index of the
%       max element, for more information see 'help max'. If your examples
%       are in rows, then, you can use max(A, [], ) to obtain the max
%       for each row.
%       

temp = X*all_theta'; %(5000,401)*(401*10)
[maxx, p] = max(temp,[],); %返回每行的最大值

% =========================================================================

end

predictOneVsAll.m

二：神经网络(Neural Networks)

　  这里已经拟合好三层网络的参数$\Theta1$和$\Theta2$，只需加载ex3weights.mat就可以了。

　　中间层(hidden layer)$\Theta1$的size为25x401，输出层( output layer)$\Theta2$的size为10x26。

　　根据前向传播算法(Feedforward Propagation)来去预测数据，

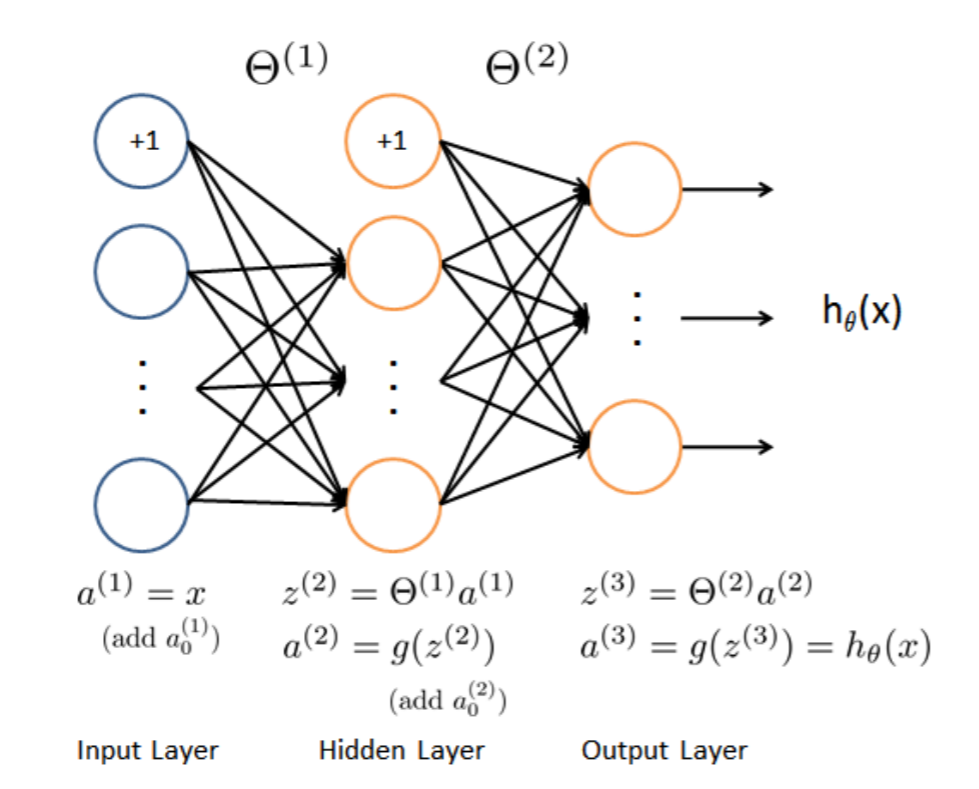
　　$z^{(2)}=\Theta^{(1)}x$

　　$a^{(2)}=g(z^{(2)})$

　　$z^{(3)}=\Theta^{(2)}a^{(2)}$

　　$a^{(3)}=g(z^{(3)})=h_\theta(x)$

　　

function p = predict(Theta1, Theta2, X)
%PREDICT Predict the label of an input given a trained neural network
%   p = PREDICT(Theta1, Theta2, X) outputs the predicted label of X given the
%   trained weights of a neural network (Theta1, Theta2)

% Useful values
m = size(X, );
num_labels = size(Theta2, );

% You need to return the following variables correctly
p = zeros(size(X, ), );

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned neural network. You should set p to a
%               vector containing labels between  to num_labels.
%
% Hint: The max function might come in useful. In particular, the max
%       function can also return the index of the max element, for more
%       information see 'help max'. If your examples are in rows, then, you
%       can use max(A, [], ) to obtain the max for each row.
%

 X=[ones(m,) X]; %而外增加一列偏差单位
 item=sigmoid(X*Theta1'); %计算a^{(2)}
 item=[ones(m,) item];
 item=sigmoid(item*Theta2');
 [a,p]=max(item,[],); %每行最大值

% =========================================================================

end

predict.m

　　最后我们可以看到，预测的准确率为97.5%。

我的便签：做个有情怀的程序员。