数据结构与算法（周测7-拓扑排序和AOV网络）

判断题

1.AOE图的关键路径就是最长的路径

    
T
    
F

2.AOE图的权值最大的边（活动）一定是关键活动。

    
T
    
F

两条边相加可能比最大的边还要大。

3.在AOE-网工程中，减少任一关键活动上的权值后，整个工期也就会相应的减小。

    
T
    
F

关键路径有多条时不一定。

4.AOE-网工程工期为关键活动上的权之和。

    
T
    
F

工期为起点到终点的最大路径长度。

5.在关键路径上的活动都是关键活动，而关键活动也必在关键路径上。

    
T
    
F

6.若图G有环，则G不存在拓扑排序序列。

    
T
    
F

存在拓扑排序和图是否有环是充分必要条件。

7.若图G为连通图且不存在拓扑排序序列，则图G必有环。

    
T
    
F

8.拓扑序一定是唯一的。

    
T
    
F

选择题

1.在AOE网中，什么是关键路径？

    A.最短回路

    B.最长回路

    C.从第一个事件到最后一个事件的最短路径

    D.从第一个事件到最后一个事件的最长路径

见定义。

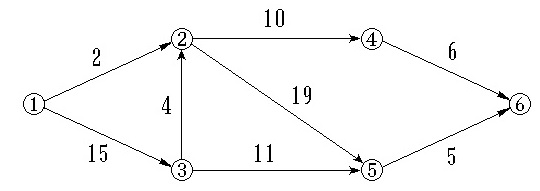
2.如图所示的AOE-网，求这个工程最早可能在什么时间结束。

    A.33

    B.18

    C.43

    D.26

关键路径为1-3-2-5-6，把权值相加为43。

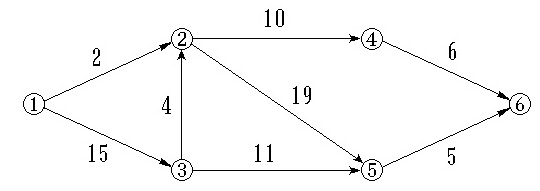
3.求如图所示的AOE-网的关键路径。

    A.

    B.

    C.

    D.

关键路径为1-3-2-5-6。

4.如图所示的AOE-网 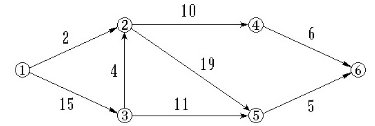，事件④的最迟发生时间是。

    A.29

    B.37

    C.38

    D.43

4的最迟发生时间为整个工程的时间减去6。

5.下图所示的 AOE 网表示一项包含 8 个活动的工程。活动 d 的最早开始时间和最迟开始时间分别是：

    A.3 和 7

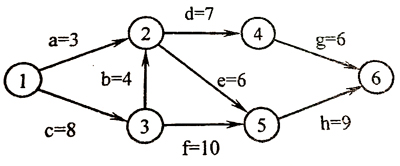
    B.12 和 12

    C.12 和 14

    D.15 和 15

d的最早开始时间为2结束后，也就是8+4=12，最迟发生时间为工程总时间27减g和d的长度。

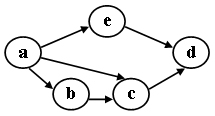
6.对下图进行拓扑排序，可以得到不同的拓扑序列的个数是：

    A.4

    B.3

    C.2

    D.1

abced,aebcd,abecd。

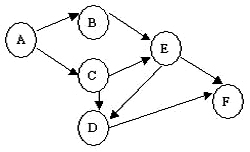
7.下图为一个AOV网，其可能的拓扑有序序列为：

    A.ACBDEF

    B.ABCEFD

    C.ABCDFE

    D.ABCEDF

8.在拓扑排序算法中用堆栈和用队列产生的结果会不同吗？

    A.是的肯定不同

    B.肯定是相同的

    C.有可能会不同

    D.以上全不对

9.设有向图有n个顶点和e条边，采用邻接表存储，进行拓扑排序时，时间复杂度为（）。

    A.O (nlog_​2e)

    B.O ( elog_​2n)

    C.O (e*n )

    D.O (n+e)

算法每次找玩度为0的点，需要O(n)，有e条边，所以顶点的入度减1一共花了O(e)，总共就是O(n+e)。

10.有拓扑排序的图一定是（）。

    A.无向图

    B.有向无环图

    C.有环图

    D.强连通图

11.判定一个有向图是否存在回路除了可以利用拓扑排序方法外，还可以利用（）。

    A.求最短路径的Dijkstra

    B.求生成树的方法

    C.深度优先遍历算法

    D.宽度优先遍历算法

深度优先搜索如果一个顶点被两次遍历就存在回路。

12.下列选项中，不是如下有向图的拓扑序列的是：

    A.1, 5, 2, 3, 6, 4

    B.5, 1, 2, 6, 3, 4

    C.5, 1, 2, 3, 6, 4

    D.5, 2, 1, 6, 3, 4