Gaussian Processes

原文地址：https://borgwang.github.io/ml/2019/07/28/gaussian-processes.html

一元高斯分布

概率密度函数：$$p(x) = \frac{1}{\sigma\sqrt{2\pi}}\mathrm{exp}(-\frac{(x-\mu)^2}{2\sigma2}) \tag{1}$$

其中\(\mu\)和\(\sigma\)分别表示均值和方差，这个概率密度函数曲线画出来就是我们熟悉的钟形曲线，均值和方差唯一地决定了曲线的形状。

多元高斯分布

从一元高斯分布推广到多元高斯分布，假设各维度之间相互独立$$p(x_1, x_2, ..., x_n) = \prod_{i=1}^{n}p(x_i) \ =\frac{1}{(2\pi)^{\frac{n}{2}}\sigma_1\sigma_2...\sigma_n}\mathrm{exp}\left(-\frac{1}{2}\left [\frac{(x_1-\mu_1)^2}{\sigma_12} + \frac{(x_2-\mu_2)^2}{\sigma_22} + ... + \frac{(x_n-\mu_n)^2}{\sigma_n2}\right]\right) \tag{2}$$其中\(\mu_1,\mu_2,\cdots\)和\(\sigma_1,\sigma_2,\cdots\)分别是第 1 维、第二维……的均值和方差。对上式向量和矩阵表示上式，令$$\boldsymbol{x - \mu}=[x_1-\mu_1, \ x_2-\mu_2,\ … \ x_n-\mu_n]^T \ K = \begin{bmatrix}

\sigma_1^2 & 0 & \cdots & 0\

0 & \sigma_2^2 & \cdots & 0\

\vdots & \vdots & \ddots & 0\

0 & 0 & 0 & \sigma_n^2

\end{bmatrix}$$

则：$$\sigma_1\sigma_2...\sigma_n = |K|^{\frac{1}{2}} \ \frac{(x_1-\mu_1)^2}{\sigma_12} + \frac{(x_2-\mu_2)^2}{\sigma_22} + ... + \frac{(x_n-\mu_n)^2}{\sigma_n2}=(\boldsymbol{x-\mu})^TK{-1}(\boldsymbol{x-\mu})$$

代入上式得到 $$p(\boldsymbol{x}) = (2\pi)^{{-\frac{n}{2}}|K|}{-\frac{1}{2}}\mathrm{exp}\left( -\frac{1}{2}(\boldsymbol{x-\mu})^TK{-1}(\boldsymbol{x-\mu}) \right) \tag{3}$$

其中\(\boldsymbol{\mu} \in \mathbb{R}^n\)是均值向量，\(K \in \mathbb{R}^{n \times n}\)为协方差矩阵，由于我们假设了各维度直接相互独立，因此\(K\)是一个对角矩阵。在各维度变量相关时，上式的形式仍然一致，但此时协方差矩阵\(K\)不再是对角矩阵，只具备半正定和对称的性质。上式通常也简写为$$x \sim \mathcal{N}(\boldsymbol{\mu}, K)$$

无限元高斯分布

用一个例子来展示这个扩展的过程:MLSS 2012: J. Cunningham - Gaussian Processes for Machine Learning

假设我们在周一到周四每天的 7:00 测试了 4 次心率，如图中 4 个点，可能的高斯分布如图所示（高瘦的曲线）。这是一个一元高斯分布，只有每天 7: 00 心率这个维度。



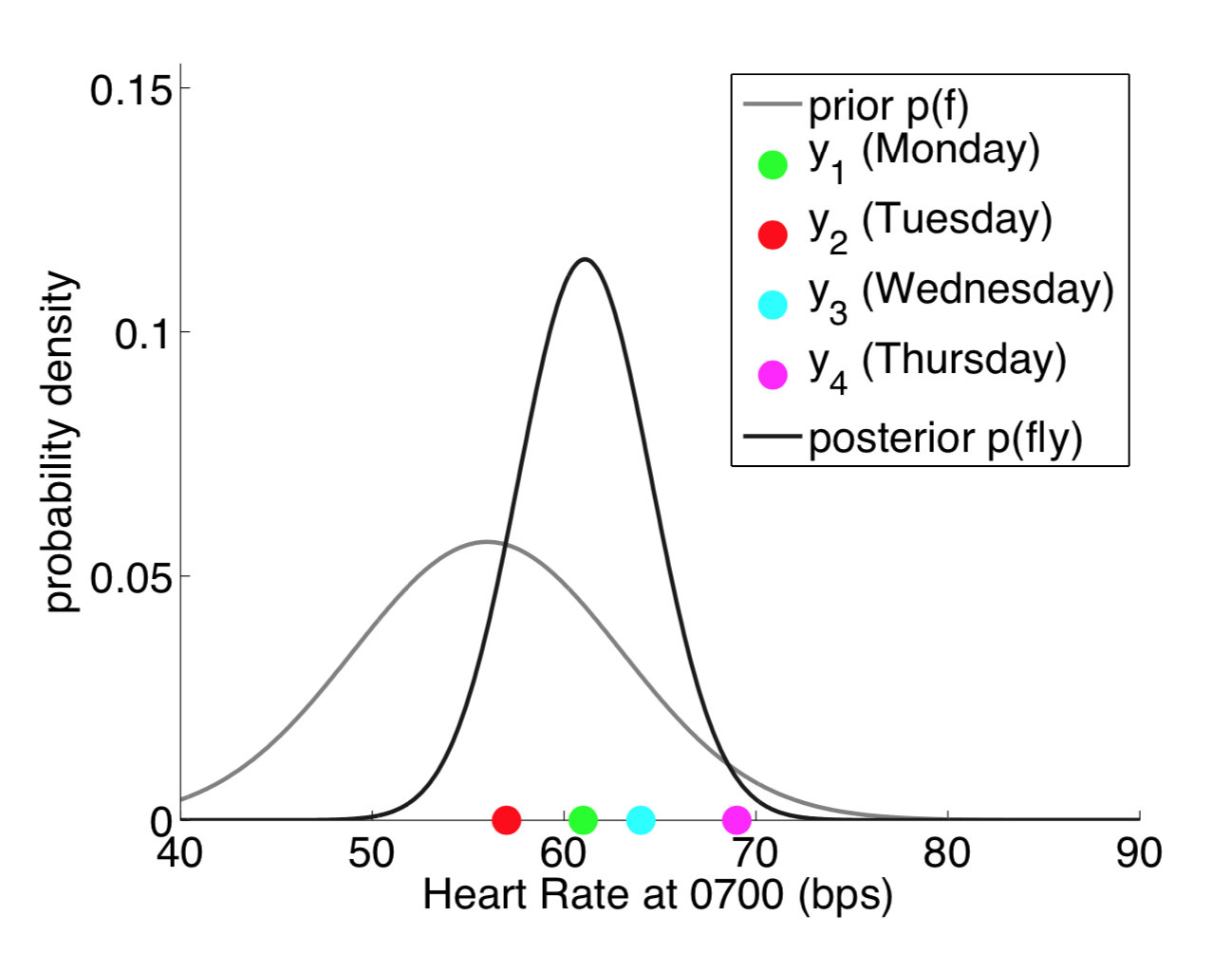
现在考虑不仅在每天的 7: 00 测心率，在 8:00 时也进行测量，这个时候变成两个维度（二元高斯分布），如图所示：



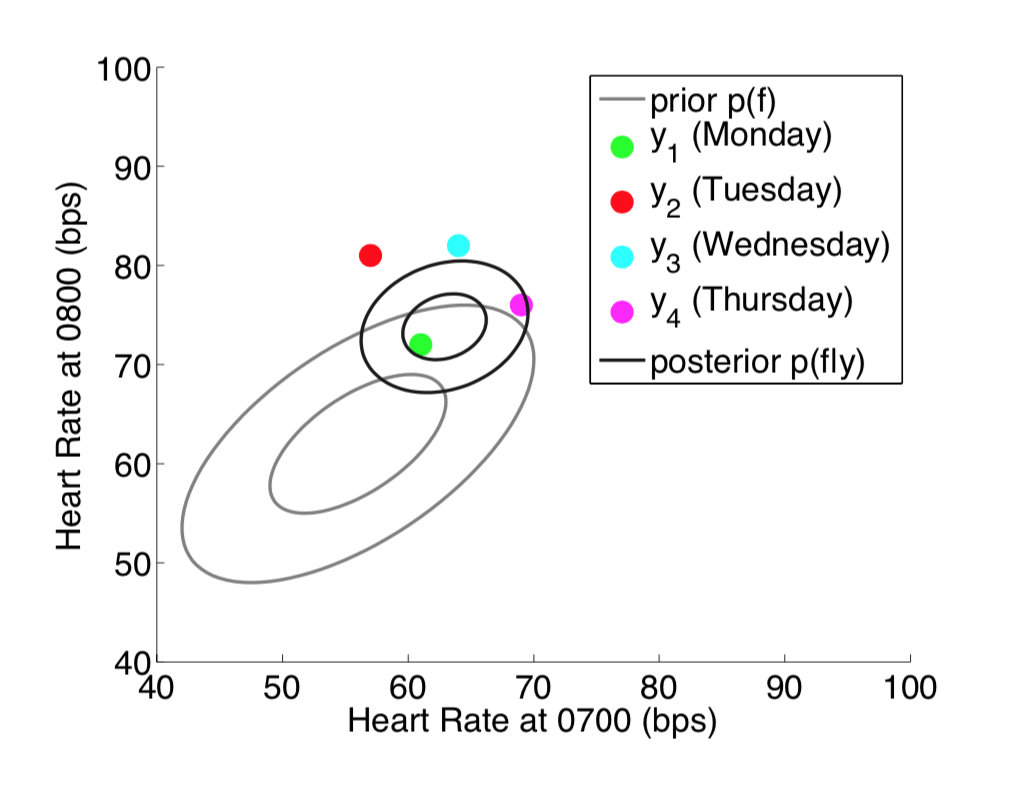
如果我们在每天的无限个时间点都进行测量，则变成了下图的情况。注意下图中把测量时间作为横轴，则每个颜色的一条线代表一个（无限个时间点的测量）无限维的采样。当对无限维进行采样得到无限多个点时，其实可以理解为对函数进行采样。



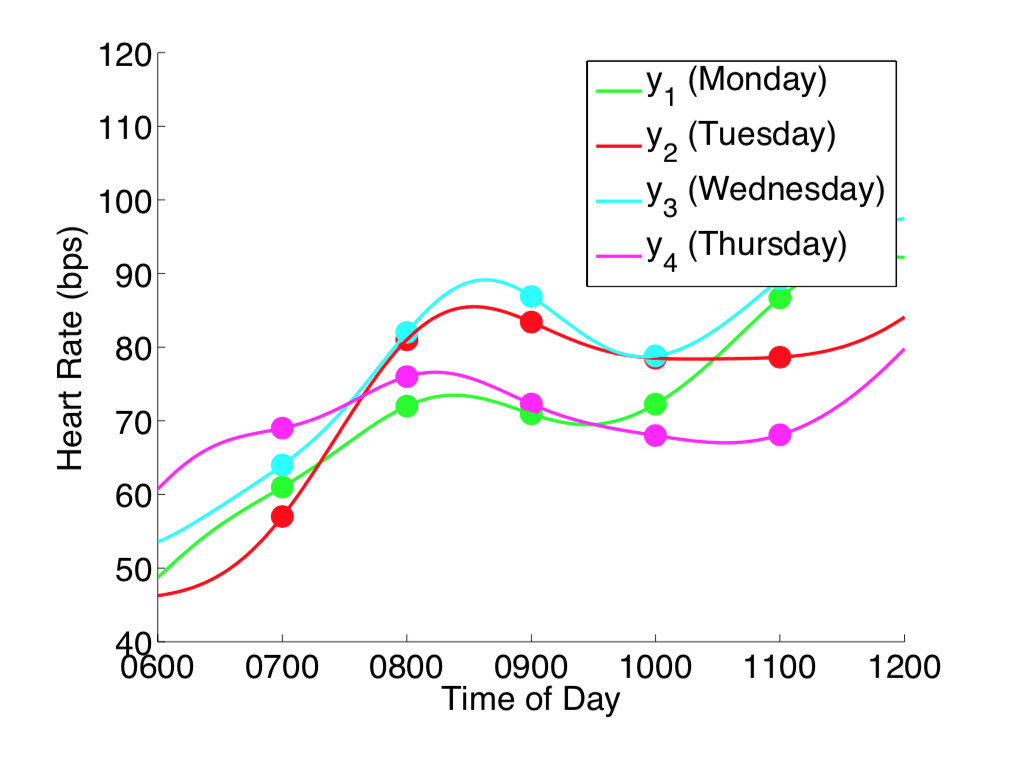
当从函数的视角去看待采样，理解了每次采样无限维相当于采样一个函数之后，原本的概率密度函数不再是点的分布 ，而变成了函数的分布。这个无限元高斯分布即称为高斯过程。

高斯过程正式地定义为：对于所有\(\boldsymbol{x} = [x_1, x_2, \cdots, x_n],f(\boldsymbol{x})=[f(x_1), f(x_2), \cdots, f(x_n)]\)都服从多元高斯分布，则称\(f\)是一个高斯过程，表示为$$f(\boldsymbol{x}) \sim \mathcal{N}(\boldsymbol{\mu}(\boldsymbol{x}), \kappa(\boldsymbol{x},\boldsymbol{x})) \tag{4}$$这里\(\boldsymbol{\mu}(\boldsymbol{x}): \mathbb{R^{n}} \rightarrow \mathbb{R^{n}}\)表示均值函数（Mean function），返回各个维度的均值；\(\kappa(\boldsymbol{x},\boldsymbol{x}) : \mathbb{R^{n}} \times \mathbb{R^{n}} \rightarrow \mathbb{R^{n\times n}}\)为协方差函数 Covariance Function（也叫核函数 Kernel Function）返回各个维度之间的协方差矩阵。一个高斯过程为一个均值函数和协方差函数唯一地定义，并且一个高斯过程的有限维度的子集都服从一个多元高斯分布（为了方便理解，可以想象二元高斯分布两个维度各自都服从一个高斯分布）。

核函数（协方差函数）

核函数是一个高斯过程的核心，核函数决定了一个高斯过程的性质。核函数在高斯过程中起的作用是生成一个协方差矩阵（相关系数矩阵），衡量任意两个点之间的“距离”。最常用的一个核函数为高斯核函数，也成为径向基函数 RBF。其基本形式如下。其中\(\sigma\)和\(l\)是高斯核的超参数。$$K(x_i,x_j)=\sigma^2\mathrm{exp}\left( -\frac{\left |x_i-x_j\right |_2^2}{2l2}\right)$$

高斯核函数的 python 实现如下：

import numpy as np

def gaussian_kernel(x1, x2, l=1.0, sigma_f=1.0):
    """Easy to understand but inefficient."""
    m, n = x1.shape[0], x2.shape[0]
    dist_matrix = np.zeros((m, n), dtype=float)
    for i in range(m):
        for j in range(n):
            dist_matrix[i][j] = np.sum((x1[i] - x2[j]) ** 2)
    return sigma_f ** 2 * np.exp(- 0.5 / l ** 2 * dist_matrix)

def gaussian_kernel_vectorization(x1, x2, l=1.0, sigma_f=1.0):
    """More efficient approach."""
    dist_matrix = np.sum(x1**2, 1).reshape(-1, 1) + np.sum(x2**2, 1) - 2 * np.dot(x1, x2.T)
    return sigma_f ** 2 * np.exp(-0.5 / l ** 2 * dist_matrix)

x = np.array([700, 800, 1029]).reshape(-1, 1)
print(gaussian_kernel_vectorization(x, x, l=500, sigma=10))

输出的协方差矩阵为

[[100.    98.02  80.53]
 [ 98.02 100.    90.04]
 [ 80.53  90.04 100.  ]]

高斯过程更新

下图是高斯过程的可视化，其中蓝线是高斯过程的均值，浅蓝色区域 95% 置信区间（由协方差矩阵的对角线得到），每条虚线代表一个函数采样（这里用了 100 维模拟连续无限维）。左上角第一幅图是高斯过程的先验（这里用了零均值作为先验），后面几幅图展示了当观测到新的数据点的时候，高斯过程如何更新自身的均值函数和协方差函数。

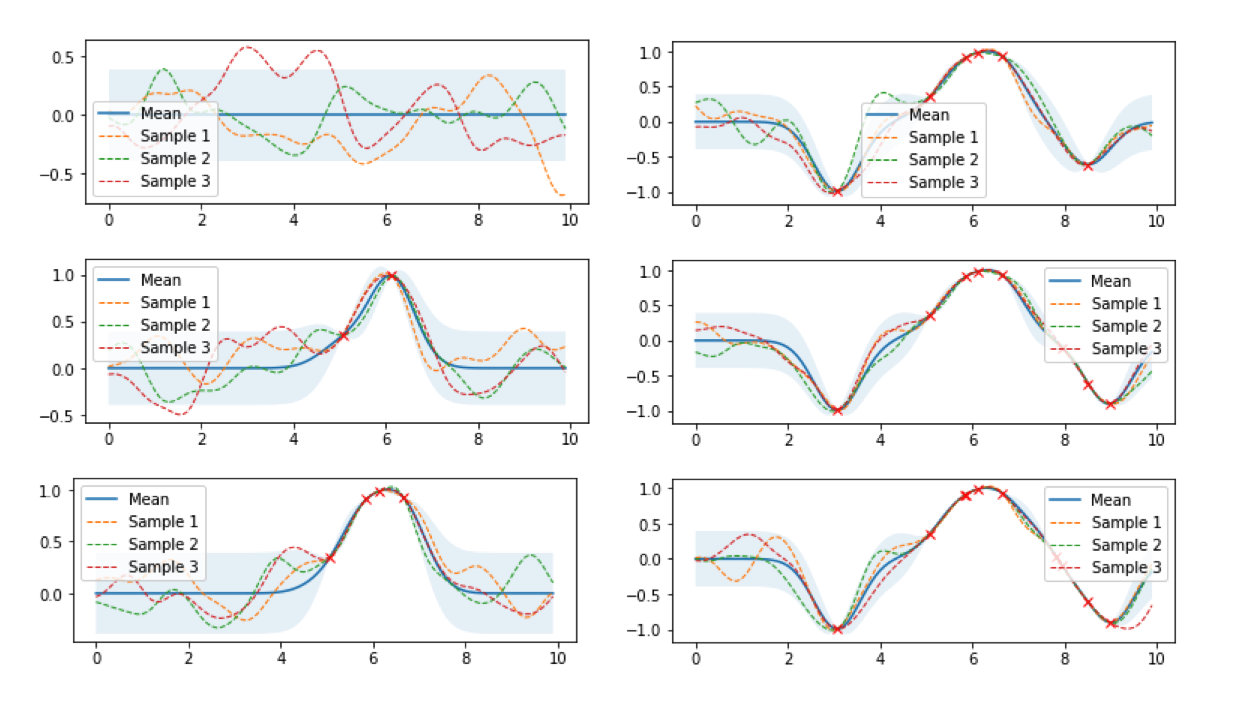
将高斯过程的先验表示为\(f(\boldsymbol{x}) \sim \mathcal{N}(\boldsymbol{\mu}_{f}, K_{ff})\)，如果现在我们观测到一些数据\((\boldsymbol{x'}, \boldsymbol{y})\)，并且假设\(\boldsymbol{y}\)与\(f(\boldsymbol{x})\)服从联合高斯分布$$\begin{bmatrix}

f(\boldsymbol{x})\

\boldsymbol{y}\

\end{bmatrix} \sim \mathcal{N} \left(

\begin{bmatrix}

\boldsymbol{\mu_f}\

\boldsymbol{\mu_y}\

\end{bmatrix},

\begin{bmatrix}

K_{ff} & K_{fy}\

K_{fy}^T & K_{yy}\

\end{bmatrix}

\right)$$

其中\(K_{ff} = \kappa(\boldsymbol{x}, \boldsymbol{x})\),\(K_{fy}=\kappa(\boldsymbol{x}, \boldsymbol{x'})\),\(K_{yy} = \kappa(\boldsymbol{x'}, \boldsymbol{x'})\)，则有$$f|\boldsymbol{y} \sim \mathcal{N}(K_{fy}K_{yy}^{{-1}\boldsymbol{y}+\boldsymbol{\mu_f},K_{ff}-K_{fy}K_{yy}}{-1}K_{fy}^T) \tag{5}$$

公式（5）表明了给定数据\((\boldsymbol{x'}, \boldsymbol{y})\)之后函数的分布\(f\)仍然是一个高斯过程。

上式其实就是高斯过程回归的基本公式，首先有一个高斯过程先验分布，观测到一些数据（机器学习中的训练数据），基于先验和一定的假设（联合高斯分布）计算得到高斯过程后验分布的均值和协方差。

简单高斯过程回归实现

考虑代码实现一个高斯过程回归，API 接口风格采用 sciki-learn fit-predict 风格。由于高斯过程回归是一种非参数化的方法，每次的 inference 都需要利用所有的训练数据进行计算得到结果，因此并没有一个显式的训练模型参数的过程，所以 fit 方法只需要将训练数据记录下来，实际的 inference 在 predict 方法中进行。Python 代码如下

from scipy.optimize import minimize

class GPR:

    def __init__(self, optimize=True):
        self.is_fit = False
        self.train_X, self.train_y = None, None
        self.params = {"l": 0.5, "sigma_f": 0.2}
        self.optimize = optimize

    def fit(self, X, y):
        # store train data
        self.train_X = np.asarray(X)
        self.train_y = np.asarray(y)
        self.is_fit = True

    def predict(self, X):
        if not self.is_fit:
            print("GPR Model not fit yet.")
            return

        X = np.asarray(X)
        Kff = self.kernel(X, X)  # (N,N)
        Kyy = self.kernel(self.train_X, self.train_X) # (k,k)
        Kfy = self.kernel(X, self.train_X)  # (N,k)
        Kyy_inv = np.linalg.inv(Kyy + 1e-8 * np.eye(len(self.train_X)))  # (k,k)

        mu = Kfy.dot(Kyy_inv).dot(self.train_y)
        cov = self.kernel(X, X) - Kfy.dot(Kyy_inv).dot(Kfy.T)
        return mu, cov

    def kernel(self, x1, x2):
        dist_matrix = np.sum(x1**2, 1).reshape(-1, 1) + np.sum(x2**2, 1) - 2 * np.dot(x1, x2.T)
        return self.params["sigma_f"] ** 2 * np.exp(-0.5 / self.params["l"] ** 2 * dist_matrix)
def y(x, noise_sigma=0.0):
    x = np.asarray(x)
    y = np.cos(x) + np.random.normal(0, noise_sigma, size=x.shape)
    return y.tolist()

train_X = np.array([3, 1, 4, 5, 9]).reshape(-1, 1)
train_y = y(train_X, noise_sigma=1e-4)
test_X = np.arange(0, 10, 0.1).reshape(-1, 1)

gpr = GPR()
gpr.fit(train_X, train_y)
mu, cov = gpr.predict(test_X)
test_y = mu.ravel()
uncertainty = 1.96 * np.sqrt(np.diag(cov))
plt.figure()
plt.title("l=%.2f sigma_f=%.2f" % (gpr.params["l"], gpr.params["sigma_f"]))
plt.fill_between(test_X.ravel(), test_y + uncertainty, test_y - uncertainty, alpha=0.1)
plt.plot(test_X, test_y, label="predict")
plt.scatter(train_X, train_y, label="train", c="red", marker="x")
plt.legend()

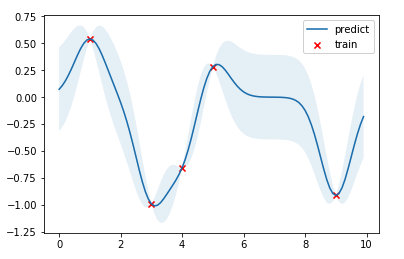
结果如下图，红点是训练数据，蓝线是预测值，浅蓝色区域是 95% 置信区间。真实的函数是一个 cosine 函数，可以看到在训练数据点较为密集的地方，模型预测的不确定性较低，而在训练数据点比较稀疏的区域，模型预测不确定性较高。

超参数优化

上文提到高斯过程是一种非参数模型，没有训练模型参数的过程，一旦核函数、训练数据给定，则模型就被唯一地确定下来。但是核函数本身是有参数的，比如高斯核的参数\(\sigma\)和\(l\)，我们称为这种参数为模型的超参数（类似于 k-NN 模型中 k 的取值）。

核函数本质上决定了样本点相似性的度量方法，进行影响到了整个函数的概率分布的形状。上面的高斯过程回归的例子中使用了\(\sigma=0.2\)和\(l=0.5\)的超参数，我们可以选取不同的超参数看看回归出来的效果。



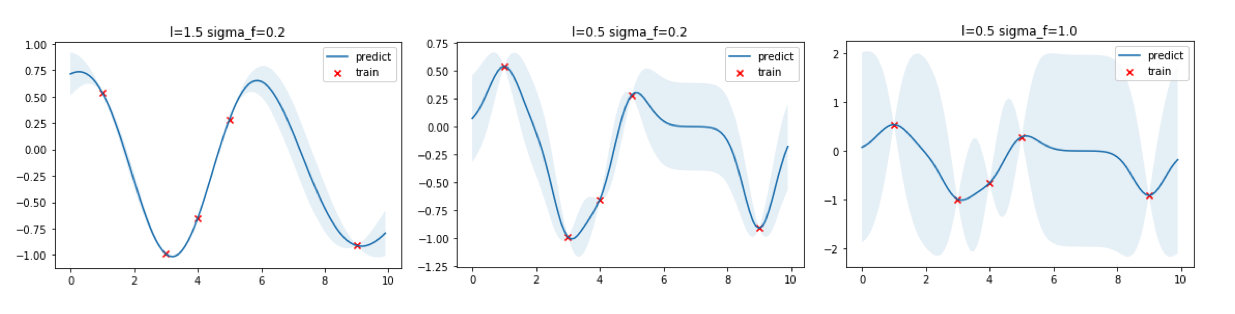
从上图可以看出，\(l\)越大函数更加平滑，同时训练数据点之间的预测方差更小，反之\(l\)越小则函数倾向于更加“曲折”，训练数据点之间的预测方差更大；\(\sigma\)则直接控制方差大小，\(\sigma\)越大方差越大，反之亦然。

如何选择最优的核函数参数\(\sigma\)和\(l\)呢？答案最大化在这两个超参数下\(y\)出现的概率，通过最大化边缘对数似然（Marginal Log-likelihood）来找到最优的参数，边缘对数似然表示为$$\mathrm{log}\ p(\boldsymbol{y}|\sigma, l) = \mathrm{log} \ \mathcal{N}(\boldsymbol{0}, K_{yy}(\sigma, l)) = -\frac{1}{2}\boldsymbol{y}^T K_{yy}^{-1}\boldsymbol{y} - \frac{1}{2}\mathrm{log}\ |K_{yy}| - \frac{N}{2}\mathrm{log} \ (2\pi) \tag{6}$$

具体的实现中，我们在 fit 方法中增加超参数优化这部分的代码，最小化负边缘对数似然。

from scipy.optimize import minimize

class GPR:

    def __init__(self, optimize=True):
        self.is_fit = False
        self.train_X, self.train_y = None, None
        self.params = {"l": 0.5, "sigma_f": 0.2}
        self.optimize = optimize

    def fit(self, X, y):
        # store train data
        self.train_X = np.asarray(X)
        self.train_y = np.asarray(y)

         # hyper parameters optimization
        def negative_log_likelihood_loss(params):
            self.params["l"], self.params["sigma_f"] = params[0], params[1]
            Kyy = self.kernel(self.train_X, self.train_X) + 1e-8 * np.eye(len(self.train_X))
            return 0.5 * self.train_y.T.dot(np.linalg.inv(Kyy)).dot(self.train_y) + 0.5 * np.linalg.slogdet(Kyy)[1] + 0.5 * len(self.train_X) * np.log(2 * np.pi)

        if self.optimize:
            res = minimize(negative_log_likelihood_loss, [self.params["l"], self.params["sigma_f"]],
                   bounds=((1e-4, 1e4), (1e-4, 1e4)),
                   method='L-BFGS-B')
            self.params["l"], self.params["sigma_f"] = res.x[0], res.x[1]

        self.is_fit = True

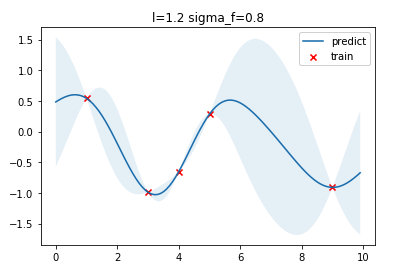
将训练、优化得到的超参数、预测结果可视化如下图，可以看到最优的\(l=1.2\)，\(\sigma_f=0.8\)



这里用 scikit-learn 的 GaussianProcessRegressor 接口进行对比

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import ConstantKernel, RBF

# fit GPR
kernel = ConstantKernel(constant_value=0.2, constant_value_bounds=(1e-4, 1e4)) * RBF(length_scale=0.5, length_scale_bounds=(1e-4, 1e4))
gpr = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=2)
gpr.fit(train_X, train_y)
mu, cov = gpr.predict(test_X, return_cov=True)
test_y = mu.ravel()
uncertainty = 1.96 * np.sqrt(np.diag(cov))

# plotting
plt.figure()
plt.title("l=%.1f sigma_f=%.1f" % (gpr.kernel_.k2.length_scale, gpr.kernel_.k1.constant_value))
plt.fill_between(test_X.ravel(), test_y + uncertainty, test_y - uncertainty, alpha=0.1)
plt.plot(test_X, test_y, label="predict")
plt.scatter(train_X, train_y, label="train", c="red", marker="x")
plt.legend()

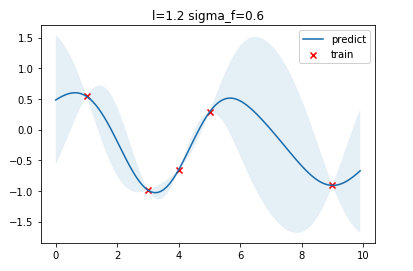
得到结果为\(l=1.2\)，\(\sigma_f=0.6\)，这个与我们实现的优化得到的超参数有一点点不同，可能是实现的细节有所不同导致。

多维输入

我们上面讨论的训练数据都是一维的，高斯过程直接可以扩展于多维输入的情况，直接将输入维度增加即可。

def y_2d(x, noise_sigma=0.0):
    x = np.asarray(x)
    y = np.sin(0.5 * np.linalg.norm(x, axis=1))
    y += np.random.normal(0, noise_sigma, size=y.shape)
    return y

train_X = np.random.uniform(-4, 4, (100, 2)).tolist()
train_y = y_2d(train_X, noise_sigma=1e-4)

test_d1 = np.arange(-5, 5, 0.2)
test_d2 = np.arange(-5, 5, 0.2)
test_d1, test_d2 = np.meshgrid(test_d1, test_d2)
test_X = [[d1, d2] for d1, d2 in zip(test_d1.ravel(), test_d2.ravel())]

gpr = GPR(optimize=True)
gpr.fit(train_X, train_y)
mu, cov = gpr.predict(test_X)
z = mu.reshape(test_d1.shape)

fig = plt.figure(figsize=(7, 5))
ax = Axes3D(fig)
ax.plot_surface(test_d1, test_d2, z, cmap=cm.coolwarm, linewidth=0, alpha=0.2, antialiased=False)
ax.scatter(np.asarray(train_X)[:,0], np.asarray(train_X)[:,1], train_y, c=train_y, cmap=cm.coolwarm)
ax.contourf(test_d1, test_d2, z, zdir='z', offset=0, cmap=cm.coolwarm, alpha=0.6)
ax.set_title("l=%.2f sigma_f=%.2f" % (gpr.params["l"], gpr.params["sigma_f"]))

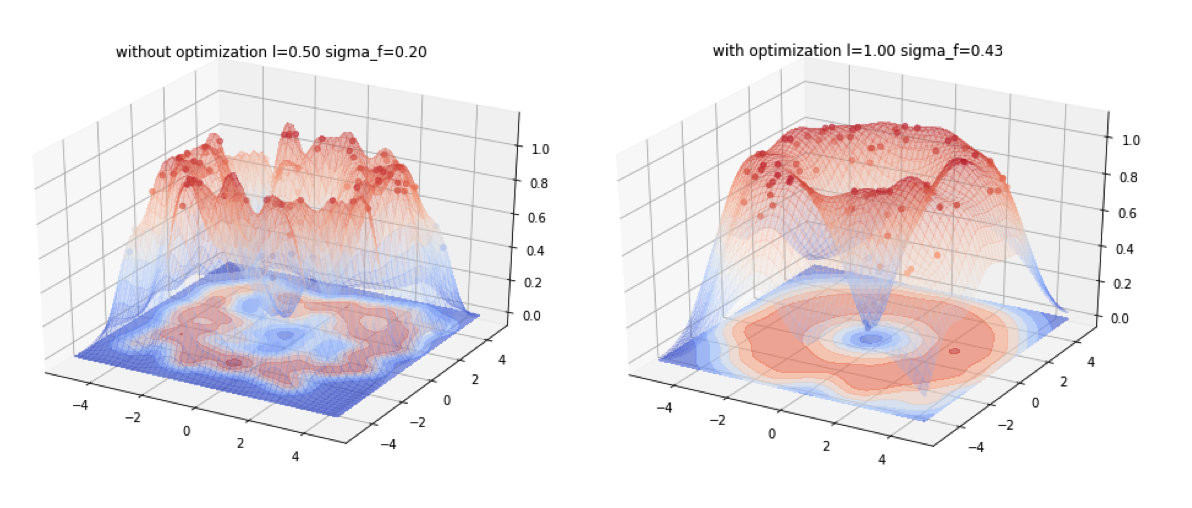
下面是一个二维输入数据的告你过程回归，左图是没有经过超参优化的拟合效果，右图是经过超参优化的拟合效果。