【arc075F】Mirrored

Portal --> arc075_f

Solution

​　　 一开始抱着“我有信仰爆搜就可以过”的心态写了一个爆搜。。

​　　 但是因为。。剪枝和枚举方式不够优秀愉快T掉了qwq

​​　　 正解还是dp。。对我已经不会dp了qwq

​　　

​​　　 首先我们可以写成一个熟悉的小学奥数形式：

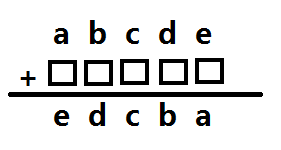
​​　　 然后比较容易注意到，确定了\(e\)代表的数值，就确定了\(a\)代表的数值（中间的那堆方框是已知的东西就是\(D\)）其他类似，也就是说我们可以对称着确定数值

​​　　 但是这里有一个东西比较的。。麻烦。。就是进位

​​　　 当然我们可以写一个爆搜暴力枚举一半然后中途剪枝通过进位之类的东西判断，但实际上注意到这个其实可以看成一个“两边向中间推进的过程”，根本没有必要爆搜，我们可以dp处理

​​　　 记\(f[i][j][k]\)表示，我们现在已经确定了前\(i\)位，第\(i+1\)位应该贡献给第\(i\)位的进位为\(j\)，第\(n-i+1\)位应该贡献给\(n-i\)位的进位为\(k\)，然后枚举范围的话就是\(i\in [1,\lfloor\frac{n}{2}\rfloor]\)，\(j\)和\(k\)都\(\in \{0,1\}\)

​​　　 然后就直接枚举第\(i+1\)位上的数字，然后算出对称过去的数字，自然也就可以算出新的贡献出的进位，然后就直接转移就好了

​​　　 最后计算答案的时候，要分位数\(n\)为奇数或偶数两种情况讨论，主要就是因为。。如果是奇数的话中间会多一位，然后这位前后都不能有进位，偶数的话只要前后进位贡献相同就好了

​　　

​​　　 代码大概长这个样子

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
using namespace std;
const int N=30;
int f[N][2][2],d[N];
int n,m,D;
ll ans;
void prework(int D){
	d[0]=0;
	while (D){
		d[++d[0]]=D%10;
		D/=10;
	}
}
ll solve(int n1){
	int n=n1/2,j1,k1,tmp,sum,mid;
	ll ret=0;
	for (int i=0;i<=n;++i)
		for (int j=0;j<2;++j)
			for (int k=0;k<2;++k)
				f[i][j][k]=0;
	f[0][0][0]=1;
	for (int i=0;i<n;++i){
		for (int j=0;j<2;++j)
			for (int k=0;k<2;++k){
				if (f[i][j][k]==0) continue;
				for (int num=0;num<=9;++num){
					sum=num+d[i+1]+k;
					tmp=sum%10; k1=sum/10;
					j1=(j*10+num)-(tmp+d[n1-i]);
					if (j1<0||j1>1) continue;
					if (!i&&(!num||!tmp)) continue;
					f[i+1][j1][k1]+=f[i][j][k];
				}
			}
	}
	if (n1%2==1){
		mid=(n1+1)/2;
		for (int j=0;j<2;++j)
			for (int k=0;k<2;++k){
				if (!f[n][j][k]) continue;
				for (int num=0;num<=9;++num){
					sum=num+d[mid]+k;
					if (sum%10==num&&sum/10==j)
						ret+=f[n][j][k];
				}
			}
	}
	else
		for (int j=0;j<2;++j)
			ret+=f[n][j][j];
	return ret;
}

int main(){
#ifndef ONLINE_JUDGE
	freopen("a.in","r",stdin);
#endif
	scanf("%d",&D);
	prework(D);
	for (int i=d[0];i<=d[0]*2;++i)
		ans+=solve(i);
	printf("%lld\n",ans);
}