Mypwd 的解读与实现 20155202

Mypwd 的解读与实现 20155202

linux下pwd命令的编写

实验要求：

• 1 学习pwd命令
• 2 研究pwd实现需要的系统调用(man -k; grep),写出伪代码
• 3 实现mypwd
• 4 测试mypwd

pwd命令含义：在Linux层次结构中，想要知道当前所处的目录，可以用pwd命令，该命令显示整个路径名。

语法：

pwd [ -L | -P ]

描述

• pwd 命令将当前目录的全路径名称（从根目录）写入标准输出。全部目录使用 /（斜线）分隔。第一个 / 表示根目录，最后一个目录是当前目录。

标志

• L

如果 PWD 环境变量包含了不包含文件名 .（点）或 ..（点点）的当前目录的绝对路径名，则显示 PWD 环境变量的值。否则，-L 标志与 -P 标志一样运行。

• P

显示当前目录的绝对路径名。与 -P 标志一起显示的绝对路径不包含在路径名的绝对路径中涉及到符号链接类型的文件的名称。

• 退出状态

该命令返回以下出口值：
0 成功完成。
>0 发生错误。

pwd的实现：

• pwd以绝对路径打印当前的工作目录。因为整个系统的文件组织是树形的，所以，可以从当前目录逐层向根目录进行查找，当找到根目录，即可得到完全路径。

1.如何逐层查找？

• 系统通过inode节点来管理文件，所以每个文件会有一个inode号。目录是比较特殊的文件，通过<inode, name>的列表组织目录下的文件。每个目录下有两个特殊的文件名".", "..",分别表示当前目录和父目录。

2.如何知道到了根目录？

• 到达根目录说明没有父目录了，但是".", ".."还是存在于根目录，只是其inode号是相同的。

3.如何打破文件系统的限制，形成完整的绝对路径？

• 查看系统所有的挂载路径，将所有挂载路径和上面求得的路径拼接起来，如果是合法路径且inode号与最初目录的inode号相同，即是想要的最终的路径。

目录的存储结构

• 每个目录下都至少有两个内容‘.’和’..’，其中‘.’代表当前目录，’..’代表上级目录。每个目录或文件都有对应的i-节点号，根目录的‘.’和’..’相同，所以i-节点号相同。通过命令’ls -1ia’(数字1，不是字母l)可以查看当前目录下的文件名和对应的i-节点号。

• (由于照片尺寸问题，请全屏看图)

• 

• 

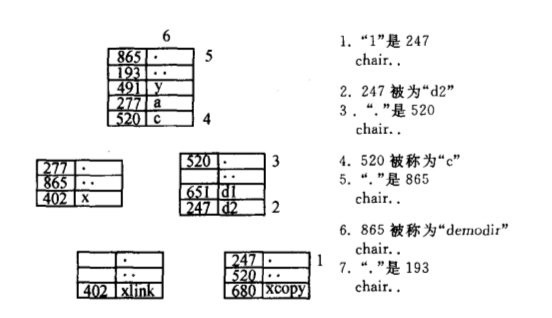
• 利用 ls -1ia查看i节点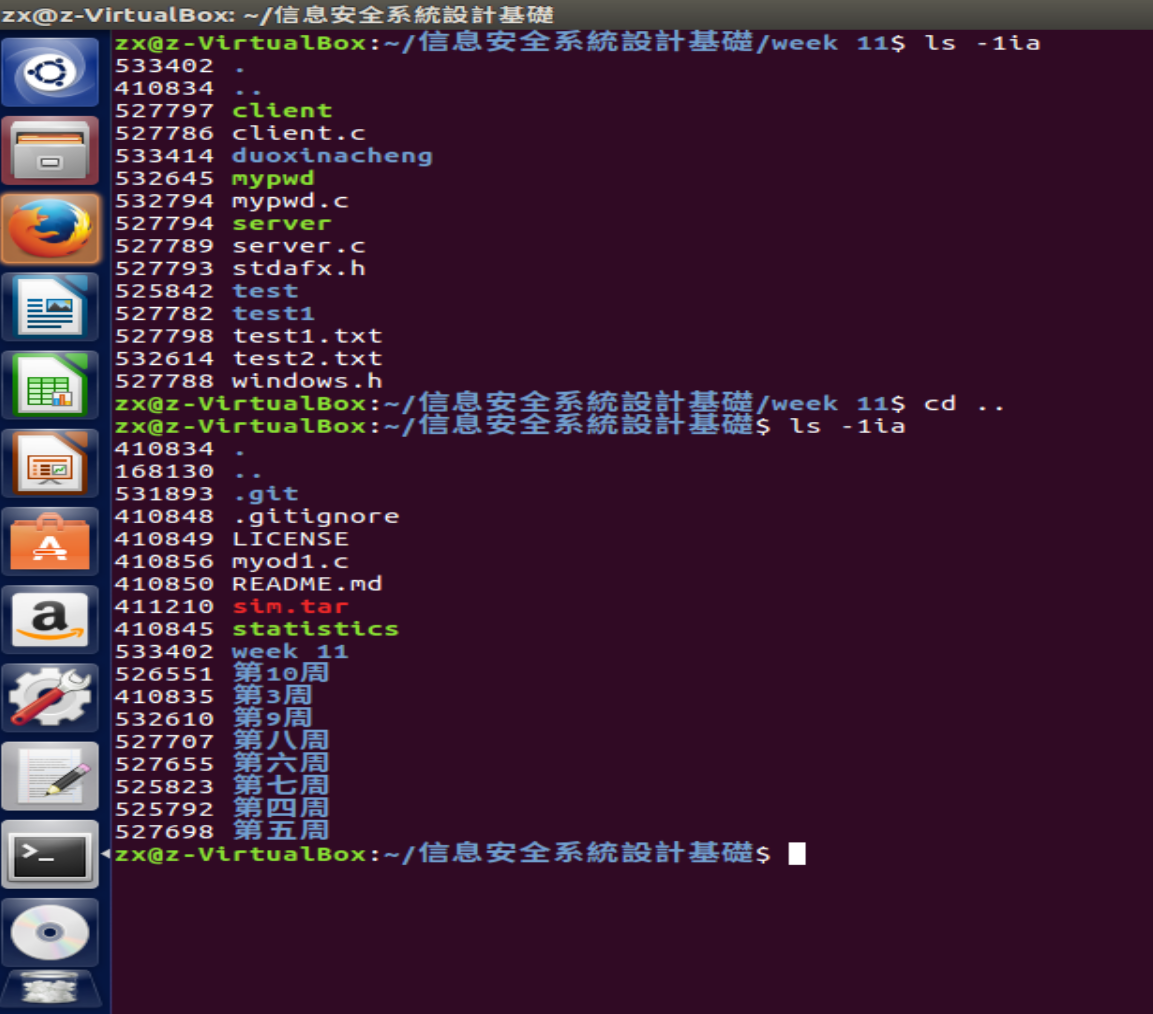

• 

• 运行结果
  
  

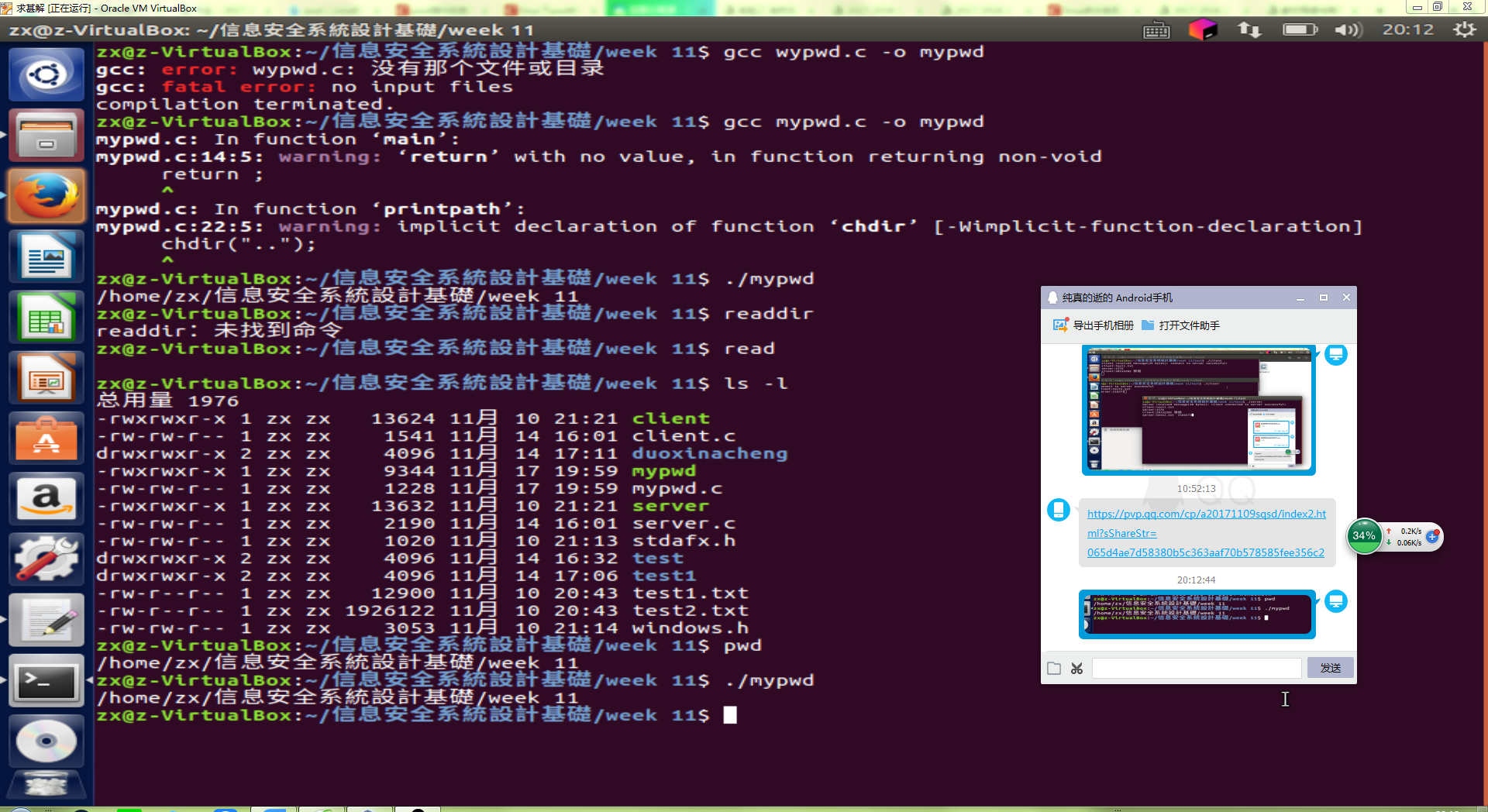
代码实现：

#include<stdio.h>
#include<sys/stat.h>
#include<dirent.h>
#include<stdlib.h>
#include<string.h>
#include<sys/types.h>
void printpath();
char *inode_to_name(int);
int getinode(char *);
int main()
{
    printpath();
    putchar('\n');
    return ;
}
void printpath()
{
    int inode,up_inode;
    char *str;
    inode = getinode(".");
    up_inode = getinode("..");
    chdir("..");
    str = inode_to_name(inode);
    if(inode == up_inode) {
    //  printf("/%s",str);
        return;
    }
    printpath();
    printf("/%s",str);
}
int getinode(char *str)
{
    struct stat st;
    if(stat(str,&st) == -1){
        perror(str);
        exit(-1);
    }
    return st.st_ino;
}
char *inode_to_name(int inode)
{
    char *str;
    DIR *dirp;
    struct dirent *dirt;
    if((dirp = opendir(".")) == NULL){
        perror(".");
        exit(-1);
    }
    while((dirt = readdir(dirp)) != NULL)
    {
        if(dirt->d_ino == inode){
            str = (char *)malloc(strlen(dirt->d_name)*sizeof(char));
            strcpy(str,dirt->d_name);
            return str;
        }
    }
    perror(".");
    exit(-1);
}

实验感想：

这次编写pwd命令使我对操作系统中的i节点的理解进一步提高，加深了我对操作系统的的理解。

代码托管