如何用Python实现常见机器学习算法-1

最近在GitHub上学习了有关python实现常见机器学习算法

目录

• 一、线性回归

　　　　1、代价函数

　　　　2、梯度下降算法

　　　　3、均值归一化

　　　　4、最终运行结果

　　　　5、使用scikit-learn库中的线性模型实现

• 二、逻辑回归

　　　　1、代价函数

　　　　2、梯度

　　　　3、正则化

　　　　4、S型函数

　　　　5、映射为多项式

　　　　6、使用的优化方法

　　　　7、运行结果

　　　　8、使用scikit-learn库中的逻辑回归模型实现

• 逻辑回归_手写数字识别_OneVsAll

　　　　1、随机显示100个数字

　　　　2、OneVsAll

　　　　3、手写数字识别

　　　　4、预测

　　　　5、运行结果

　　　　6、使用scikit-learn库中的逻辑回归模型实现

• 三、BP神经网络

　　　　1、神经网络model

　　　　2、代价函数

　　　　3、正则化

　　　　4、反向传播BP

　　　　5、BP可以求梯度的原因

　　　　6、梯度检查

　　　　7、权重的随机初始化

　　　　8、预测

　　　　9、输出结果

• 四、SVM支持向量机

　　　　1、代价函数

　　　　2、Large Margin

　　　　3、SVM Kernel

　　　　4、使用中的模型代码

　　　　5、运行结果

• 五、K-Mearns聚类算法

　　　　1、聚类过程

　　　　2、目标函数

　　　　3、聚类中心的选择

　　　　4、聚类个数K的选择

　　　　5、应用——图片压缩

　　　　6、使用scikit-learn库中的线性模型实现聚类

　　　　7、运行结果

• 六、PCA主成分分析（降维）

　　　　1、用处

　　　　2、2D-->1D,nD-->kD

　　　　3、主成分分析PCA与线性回归的区别

　　　　4、PCA降维过程

　　　　5、数据恢复

　　　　6、主成分个数的选择（即要降的维度）

　　　　7、使用建议

　　　　8、运行结果

　　　　9、使用scikit-learn库中的PCA实现降维

• 七、异常检测Anomaly Detection

　　　　1、高斯分布（正态分布）

　　　　2、异常检测算法

　　　　3、评价的好坏，以及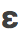的选取

　　　　4、选择使用什么样的feature（单位高斯分布）

　　　　5、多元高斯分布

　　　　6、单元和多元高斯分布特点

　　　　7、程序运行结果

一、线性回归

1、代价函数

其中。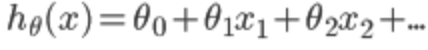

下面就是求出theta，使代价最小，即代表我们拟合出来的方程距离真实值最近共有m条数据，其中代表我们拟合出来的方程到真实值距离的平方，平方的原因是因为可能有负值，系数2的原因是下面求梯度是对每个变量求偏导，2可以消去。

代码实现：

 # 计算代价函数
 def computerCost(X,y,theta):
     m = len(y)
     J = 0
     J = (np.transpose(X*theta-y))*(X*theta-y)/(2*m) #计算代价J
     return J

注意这里的X是真实数据前加了一列1，因为有theta(0)

2、梯度下降算法

代价函数对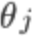求偏导得到：

所以对theta的更新可以写成：

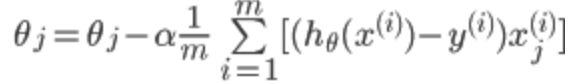
其中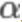为学习速率，控制梯度下降的速度，一般取0.01，0.03，0.1，0.3......

为什么梯度下降可以逐步减小代价函数？

假设函数f(x)的泰勒展开：f(x+△x)=f(x)+f'(x)*△x+o(△x),令:△x=-α*f'(x),即负梯度方向乘以一个很小的步长α，将△x带入泰勒展开式中：

f(x+x)=f(x)-α*[f'(x)]²+o(△x)

可以看出，α是取得很小的正数，[f'(x)]²也是正数，所以可以得出f(x+△x)<=f(x)，所以沿着负梯度放下，函数在减小，多维情况一样。

 # 梯度下降算法
 def gradientDescent(X,y,theta,alpha,num_iters):
     m = len(y)
     n = len(theta)
     temp = np.matrix(np.zeros((n,num_iters)))   # 暂存每次迭代计算的theta，转化为矩阵形式
     J_history = np.zeros((num_iters,1)) #记录每次迭代计算的代价值

     for i in range(num_iters):  # 遍历迭代次数
         h = np.dot(X,theta)     # 计算内积，matrix可以直接乘
         temp[:,i] = theta - ((alpha/m)*(np.dot(np.transpose(X),h-y)))   #梯度的计算
         theta = temp[:,i]
         J_history[i] = computerCost(X,y,theta)      #调用计算代价函数
         print '.',
     return theta,J_history

3、均值归一化

均值归一化的目的是使数据都缩放到一个范围内，便于使用梯度下降算法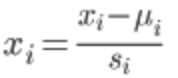

其中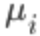为所有此feature数据的平均值，可以为此feature的最大值减去最小值，也可以为这个feature对应的数据的标准差。

代码实现：

 # 归一化feature
 def featureNormaliza(X):
     X_norm = np.array(X)            #将X转化为numpy数组对象，才可以进行矩阵的运算
     #定义所需变量
     mu = np.zeros((1,X.shape[1]))
     sigma = np.zeros((1,X.shape[1]))

     mu = np.mean(X_norm,0)          # 求每一列的平均值（0指定为列，1代表行）
     sigma = np.std(X_norm,0)        # 求每一列的标准差
     for i in range(X.shape[1]):     # 遍历列
         X_norm[:,i] = (X_norm[:,i]-mu[i])/sigma[i]  # 归一化

     return X_norm,mu,sigma

注意预测的时候也需要均值归一化数据

4、最终运行结果

代价随迭代次数的变化

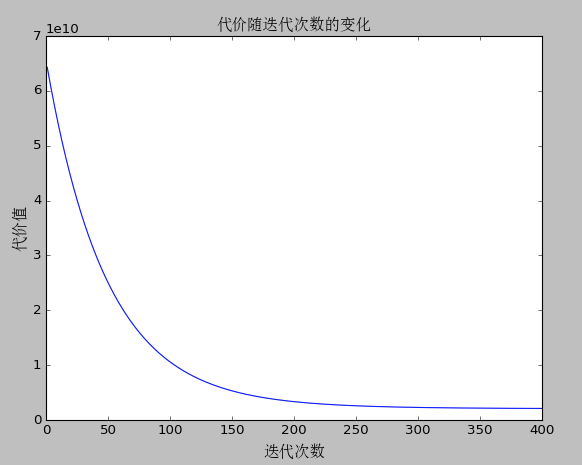
5、使用scikit-learn库中的线性模型实现

 #-*- coding: utf-8 -*-
 import numpy as np
 from sklearn import linear_model
 from sklearn.preprocessing import StandardScaler    #引入归一化的包

 def linearRegression():
     print u"加载数据...\n"
     data = loadtxtAndcsv_data("data.txt",",",np.float64)  #读取数据
     X = np.array(data[:,0:-1],dtype=np.float64)      # X对应0到倒数第2列
     y = np.array(data[:,-1],dtype=np.float64)        # y对应最后一列  

     # 归一化操作
     scaler = StandardScaler()
     scaler.fit(X)
     x_train = scaler.transform(X)
     x_test = scaler.transform(np.array([1650,3]))

     # 线性模型拟合
     model = linear_model.LinearRegression()
     model.fit(x_train, y)

     #预测结果
     result = model.predict(x_test)
     print model.coef_       # Coefficient of the features 决策函数中的特征系数
     print model.intercept_  # 又名bias偏置,若设置为False，则为0
     print result            # 预测结果

 # 加载txt和csv文件
 def loadtxtAndcsv_data(fileName,split,dataType):
     return np.loadtxt(fileName,delimiter=split,dtype=dataType)

 # 加载npy文件
 def loadnpy_data(fileName):
     return np.load(fileName)

 if __name__ == "__main__":
     linearRegression()