3D游戏与计算机图形学中的数学方法-四元数

说实话关于四元数这一节真的是不好懂，因为里面涉及到好多数学知识，单说推出来的公式就有很多。不怕大家笑话，对于四元数的学习我足足花了两天的时间，包括整理出这篇文章。在前面一章我写到了“变换”，这也是总结的学习笔记。我发现，写博客真是的是一个好多学习方法，加上之前一个博士师兄告诉我，要想好好的学习一本书或者一门技术，那么以此将学习笔记或者经验写成博客专栏是一种有效的方法。现在我要坚持这种方式，给自己留下学习过程中的足迹，也给大家分享一下。欢迎大家指出其中的不足，谢谢！

四元数是表示旋转的另一种数学形式，使用四元数可以节省存储空间，其之间的连接运算需要的算术运算更少，在产生平滑的三维动画时，用四元数更容易进行修改。

四元数集合，在数学上被称为哈密顿四元数环(ring of Hamiltonian quaternions)，用H表示，可以理解为四维空间向量，空间中的元素q可以表示为：

q = (x,y,z,w) = w + xi +yj + zk;

也可以用实数和向量的形式进行表示，即：

q = w + v;其中w是实数部分，v是v(x,y,z)。

四元数集合是复数集合的自然扩展。四元数的乘法服从分配率，并且虚部i,j,k之间满足一下关系：

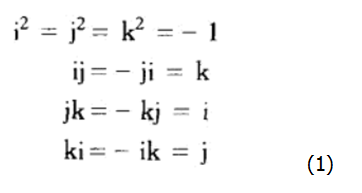
四元数式的乘法不满足交换律，因此在进行乘法运算时要注意顺序。两个四元数q₁ = w₁ + x₁i + y₁j + z₁k和q₂ = w₂ + x₂i + y₂j＋z₂k的乘积q₁q2为：

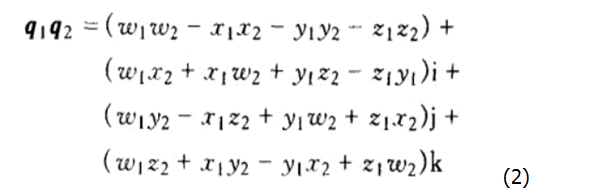
用数量-向量的形式，则q₁=s₁+v₁和q₂=s₂+v₂的乘积表达式为：

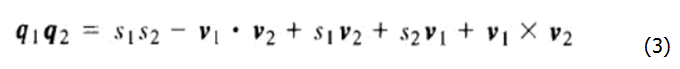
四元数也有共轭，比如一个四元数为 q = s+v，那么它的共轭为q’ = s-v。而qq’=||q||² = q².

非零的四元数的逆，记作q^-1，所以。

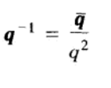
重点来了，下面；来说一下四元数的旋转

三维空间的旋转可以理解为R³到自身的映射函数φ。由于φ代表旋转，所以它必须包含长度，角度，旋转方向等信息。

如果有则长度保持不变。

如果对任意两个点p₁和p₂有

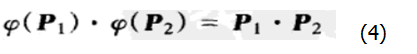
则从原点到两个点p₁和p₂的连线所形成 夹角保持不变。

如果  

则手向性也保持不变。

如果满足条件φ(s+v) = s+φ(v)，则函数φ可以扩展为H到自身的映射，这样就将(4)式改写为

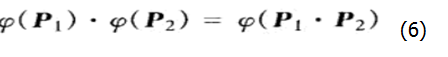
如果将p₁和p₂看做是数量部分为零的四元数，根据，就可以将(5),(6)式合并成一个等式，在该等式中可以保持角度和手向性不变，等式如下：

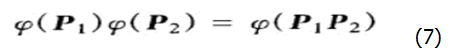
满足(7)是的函数φ称为是同态的。

该类函数φ可以用公式(8)表示：

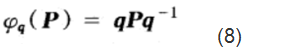
其中q为一个非零的四元数，且满足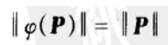和，因此可以表示旋转的集合。证明过程如下：

首先证明φq的长度保持不变，因为

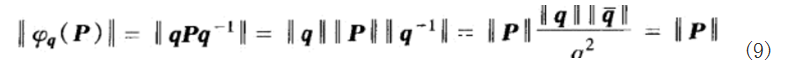
其次，φq是同态的，因为

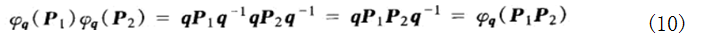
四元数与旋转的关系

假设向量P绕一任意旋转轴的单位向量A(x_a,y_a,z_a)旋转θ角，如下图所示：

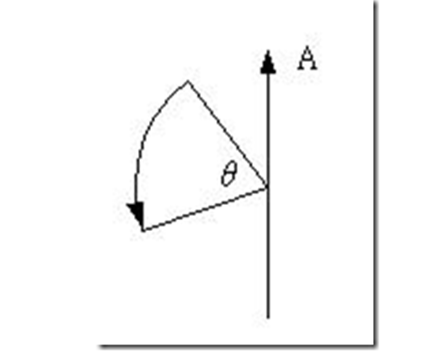
我们可以将P看作为没有实数部分的四元数xi+yj+zk,设q = s+v,则q^-1 = s-v。

那么φq(P) = qPq^-1就等于(s+v)P(s-v)。即计算过程如下所示：

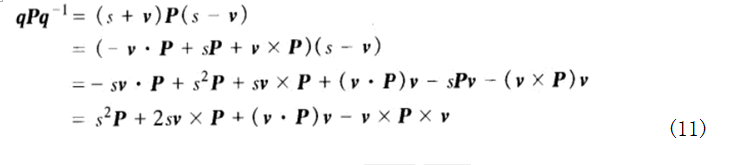
由于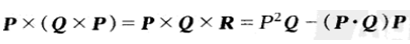则(11)等于：

设v = tA，则上式可以改写为：

将(13)与绕任意轴旋转的公式P’ = PcosΘ + (A x P)sinΘ + A(A.P)(1-cosΘ)，可以推出

则可以得到：

，

带入q = s+v得到：

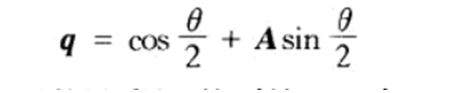
推广一下来讲：

对于四元数q的任意数量乘积表示的都是相同的旋转，因为：

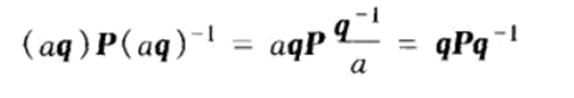
两个四元数q1和q2的乘积也可以表示一个旋转。乘积q1q2表示现已q2，后以q1进行旋转。因为：

可以将多个四元数结合起来，形成一系列旋转的一个四元数。将两个四元数相乘需要做16次乘法和加法运算，而两个3×3矩阵相乘就需要做27次类似的操作。因此对物体进行多次旋转时，应用四元数可以获得较高的计算效率。

如何将一个四元数变换成等价的3×3旋转矩阵的形式呢？

首先将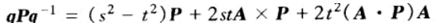改写成矩阵的形式

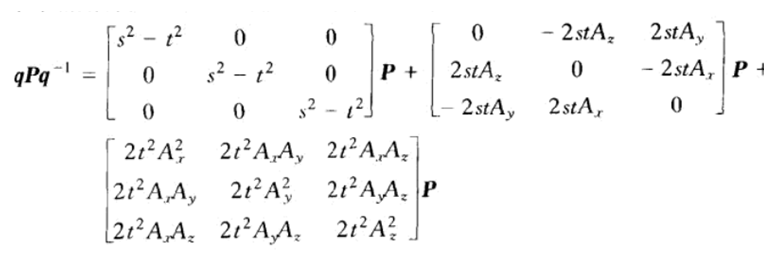
将四元数q改写成四维向量q = (w,x,y,z)，那么w = s，x = tA_x,y = tA_y,z = tA_z。因为A是单位向量，所以x²+y²+z² = t²A² = t²。

则上式等价于：

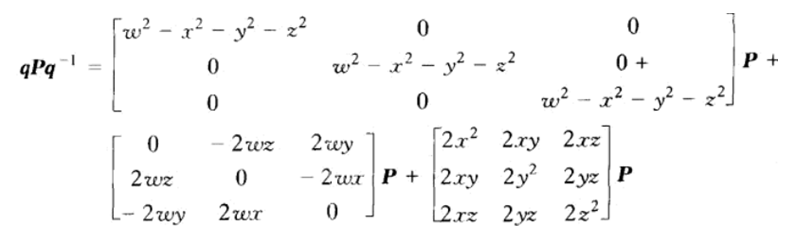
因为q是单位四元数，满足w²+ x²+y²+z² =1,所以可以得到：

则四元数的旋转矩阵R_q的公式如下：

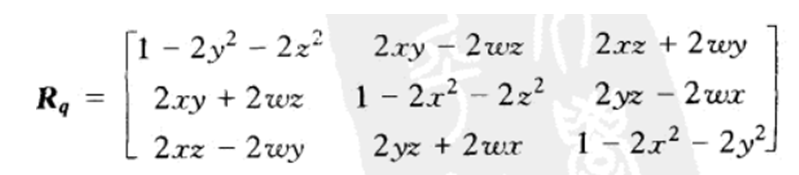
球型线性插值

因为四元数是用向量表示的，所以很适合做插值运算。在产生一个物体动画过程中，在产生位于两个预先计算的关键帧之间的中间过渡定位时，插值非常有用。

最简单的差值类型是线性插值。对于两个四元数q₁和q₂，线性插值后得到的四元数q(t)为：

当t在[0,1]范围内取值时，函数q(t)在连接q₁和q₂的线段上平滑变化。如下图所示：

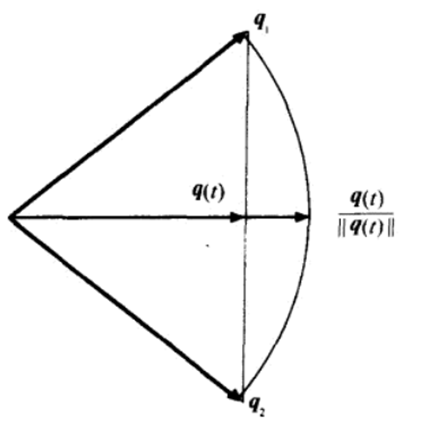
q(t)并不保持q1和q2的单位长度，但可以使用下面的函数在任意点位置对q(t)进行重新规格化：

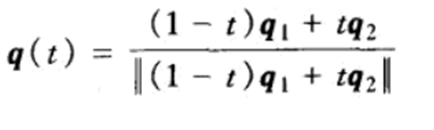
这样就可以用该函数描绘位于q₁和q₂间的过渡弧线。在上图中，它将弧描绘成四维单位超球面的二维截面。

尽管线性插值很有效，但是q(t)并没有以恒定的速率描绘q₁和q₂间的过渡弧线，这就是线性插值的弊端。下图关于cos^-1(q(t).q1)的图形表明，q₁和q₂之间的角度变化速率在端点t = 0 和 t = 1时相对较慢，而在t = 1/2时最快。

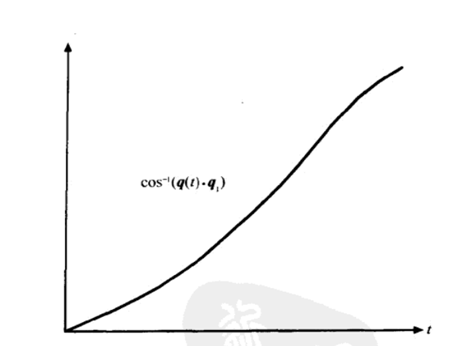
我们希望找到一个函数q(t)，用它对四元数q₁和q₂进行插值时，会保持其单位长度不变并且以恒定的速率扫过位于q₁和q₂之间的夹角。如果q₁和q₂的夹角为θ，那么这个函数将会产生一个四元数，该四元数在q(t)和q₁的形成一个夹角θ_t，这里t在0到1之间取值。

如下图(a),(b):四元数q(t)位于连接q₁和q₂的弧上，与q₁的形成一个夹角θ_t，与q2构成夹角θ_(1-t)。可以将q(t)写成：

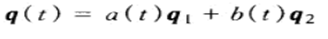
其中a(t)和b(t)分别表示q(t)在q₁和q₂方向上的分量的长度。

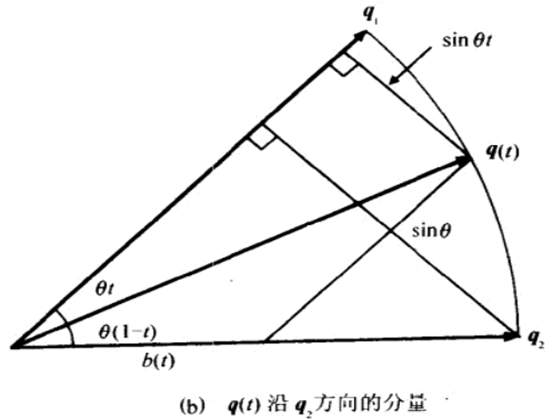
我们可以构造相似三角形来确定长度a(t),q₁到以原点和q₂为端点的线段的垂直距离为||q₁||sinθ,而q(t)到该线段的垂直距离为||q₁||sinθ(1-t)。根据相似三角形，可以得到以下关系式：

由于||q₁|| = 1，||q(t)|| = 1，可以将上式化简为：

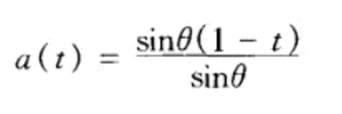
同理可以得到：

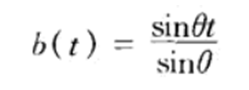
这时可以将球型线性插值函数q(t)定义为：

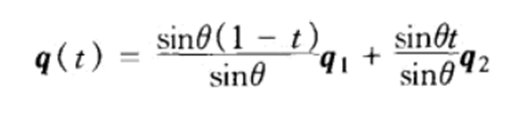
θ角为

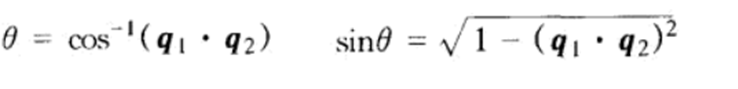
因为四元数q和-q表示相同的旋转，所以在旋转四元数q₁和q₂的正负号时一般要满足q₁.q₂>=0，这样也可以保证以最短路径的方式进行插值。