吴恩达深度学习笔记（deeplearning.ai）之循环神经网络（RNN）（三）

1. 导读

本节内容介绍普通RNN的弊端，从而引入各种变体RNN，主要讲述GRU与LSTM的工作原理。
事先声明，本人采用ng在课堂上所使用的符号系统，与某些学术文献上的命名有所不同，不过核心思想都是相同的。

2. 普通RNN的弊端

• 在NLP中，句子内部以及句子之间可能存在很长的依赖关系（long-term dependecies），最前边的单词对句子后面的单词产生影响。但是普通RNN不擅长捕获这种长期依赖关系。因为RNN相当于很深的权重共享的神经网络，因此在反向传播的过程中存在很严重的梯度消失现象，损失函数得到的输出误差很难影响到前面层的计算。

• 对于深度神经网络，不光存在梯度消失，也存在梯度爆炸的现象，以至于网络参数崩溃（当参数梯度指数级增长时，你会看到很多参数值为NaN，这意味着网络发生了数值溢出）。普通RNN也是如此，但是相比于梯度消失，梯度爆炸比较容易解决，可以采用梯度修剪（gradient clipping）的处理方法。

  梯度修剪，指当梯度向量大于某个阈值时，re-scale梯度向量，保证它不会数值爆炸。

3. GRU

3.1 简化GRU（便于理解）

与普通RNN相比，GRU添加了门控单元，改变了RNN的隐藏层，使得其能更好捕获长距离依赖关系，并且有效解决了梯度消失问题。下面对GRU进行详细的介绍：

• 在GRU中，人们引入了新的概念，memory cell，用符号\(c\)来表示，其提供了记忆能力。比如在英文句子中，网络能够记住前文的主语是单数还是复数，因此当网络看到之后的动词，仍然可以联想到前文的主语 。
• 在GRU中，\(t\)时刻有\(c^{<t>}=a^{<t>}\)，\(a^{<t>}\)是t时刻的激活值。尽管这两个值相同，我们仍然用两个不同的符号来表示，因为其分别是记忆细胞的值与输出的激活值，在LSTM中二者并不相同。 在每个时间戳，我们将用一个候选值\(\tilde{c}^{<t>}\)重写记忆细胞，每一时刻都对其进行更新。
• 在每个时间戳\(t\)中，需要用上一时刻的记忆细胞\(c^{<t-1>}\)，以及当前时刻的候选值\(\tilde{c}^{<t>}\)，来更新当前时刻的记忆细胞\(c^{<t>}\)。
• GRU最重要的思想是让我们拥有了一个叫做\(\gamma_u\)（下标\(u\)代表更新门 ）的门，该值位于0到1之间，该门用来决定，在每个时刻该如何更新记忆细胞的值。

以下是简化GRU的计算公式：
\[\tilde{c}^{<t>}=tanh(W_c[c^{<t-1>},x^{<t>}]+b_c)\]
\[\gamma_u = \sigma (W_u[c^{<t-1>},x^{<t>}]+b_u)\]
\[c^{<t>}=\gamma_u * \tilde{c}^{<t>} + (1-\gamma_u) * c^{<t-1>}\]
\[a^{<t>} = c^{<t>}\]

GRU实现细节：

• \(c^{<t>}\)、\(\tilde{c}^{<t>}\)、\(\gamma_u\)是具有相同维度的向量，因此在更新\(c^{<t>}\)时，\(\gamma_u * \tilde{c}^{<t>}\)中的\(*\)代表向量间的点乘操作。

3.2 Full GRU （完整版本）

通过上文的介绍，相信你已经对GRU有了简单的理解，出于入门的考虑，上述GRU并不完整，这里将介绍其余下的部分。
以下是完整GRU的计算公式：
\[\tilde{c}^{<t>}=tanh(W_c[\gamma_r * c^{<t-1>},x^{<t>}]+b_c)\]
\[\gamma_u = \sigma (W_u[c^{<t-1>},x^{<t>}]+b_u)\]
\[\gamma_r = \sigma (W_r[c^{<t-1>},x^{<t>}]+b_r)\]
\[c^{<t>}=\gamma_u * \tilde{c}^{<t>} + (1-\gamma_u) * c^{<t-1>}\]
\[a^{<t>} = c^{<t>}\]

这里引入了另一个门\(\gamma_r\)——the relevance gate。

ng在课上讲，可以认为r代表相关性，\(\gamma_r\)门告诉你计算出的\(\tilde{c}^{<t>}\)与\(c^{<t-1>}\)有多大的相关性。

我对GRU中“门”这一概念的理解如下：

• 无论是\(\gamma_u\)，还是\(\gamma_r\)，其本质都是一个线性函数通过激活函数（sigmoid）得到的激活值，而该线性函数是以\(x^{<t>}\)，\(c^{<t-1>}\)作为输入。
• 也就是说，每个门的向量值是由\(x^{<t>}\)，\(c^{<t-1>}\)这两个值以及线性函数的权重、偏置计算得到的。
• 反向传播通过梯度下降改变线性函数的参数来改变门的向量值。

4. LSTM

LSTM存在很多变体，这里介绍经典LSTM。

4.1 经典LSTM

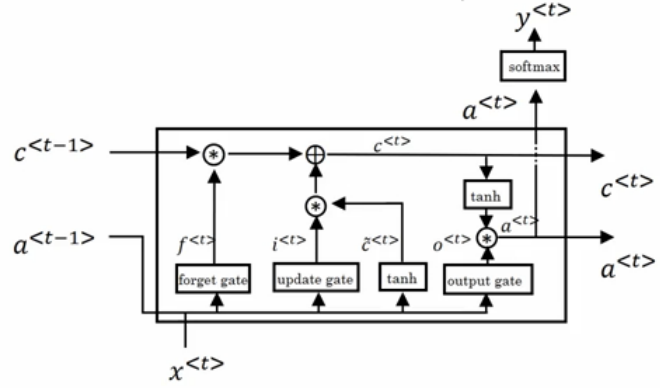
LSTM的计算公式如下所示（\(a^{<t>}\)指时刻t的隐状态）：
\[\tilde{c}^{<t>}=tanh(W_c[a^{<t-1>},x^{<t>}]+b_c)\]
\[\gamma_u = \sigma (W_u[a^{<t-1>},x^{<t>}]+b_u)\]
\[\gamma_f = \sigma (W_f[a^{<t-1>},x^{<t>}]+b_f)\]
\[\gamma_o = \sigma (W_o[a^{<t-1>},x^{<t>}]+b_o)\]
\[c^{<t>}=\gamma_u * \tilde{c}^{<t>} + \gamma_f * c^{<t-1>}\]
\[a^{<t>} = \gamma_o * tanh(c^{<t>})\]

LSTM与GRU的区别：

• LSTM中有三个门，分别是更新门\(\gamma_u\)，遗忘门\(\gamma_f\)，输出门\(\gamma_o\)。
• LSTM中使用遗忘门\(\gamm_f\)，来代替GRU中的系数\((1-\gamma_u)\)，这样是的模型更加完备，但是也引入更多的学习参数。
• LSTM的三个门，实际上是线性函数的激活值（sigmoid），而线性函数的输入是\(a^{t-1}\)，\(x^{<t>}\)。

有些论文提到了peephole connection这一概念，其目的是为了LSTM在计算门值的时候能够获得上一时刻\(c^{<t-1>}\)的信息，即将线性函数的输入扩增为\(a^{t-1}\)，\(x^{<t>}\)，\(c^{<t-1>}\)。

\(c^{<t-1>}\)与\(\gamma_u\)、\(\gamma_f\)、\(\gamma_o\)是维度相同的向量。\(c^{<t-1>}\)的每个维度，与三个门的每个维度一一对应，\(c^{<t-1>}\)中每个维度的数值只会影响到三个门中对应维度的数值。