[CLPR]BP神经网络的C++实现

文章翻译自: http://www.codeproject.com/Articles/16650/Neural-Network-for-Recognition-of-Handwritten-Digi

如何在C++中实现一个神经网络类?

主要有四个不同的类需要我们来考虑:

1. 层 - layers
2. 层中的神经元 - neurons
3. 神经元之间的连接 - connections
4. 连接的权值 - weights

这四类都在下面的代码中体现, 集中应用于第五个类 - 神经网络(neural network)上. 它就像一个容器, 用于和外部交流的接口. 下面的代码大量使用了STL的vector.

// simplified view: some members have been omitted,
// and some signatures have been altered

// helpful typedef's

typedef std::vector< NNLayer* >  VectorLayers;
typedef std::vector< NNWeight* >  VectorWeights;
typedef std::vector< NNNeuron* >  VectorNeurons;
typedef std::vector< NNConnection > VectorConnections;

// Neural Network class

class NeuralNetwork
{
public:
    NeuralNetwork();
    virtual ~NeuralNetwork();

    void Calculate( double* inputVector, UINT iCount,
        double* outputVector = NULL, UINT oCount =  );

    void Backpropagate( double *actualOutput,
         double *desiredOutput, UINT count );

    VectorLayers m_Layers;
};

// Layer class

class NNLayer
{
public:
    NNLayer( LPCTSTR str, NNLayer* pPrev = NULL );
    virtual ~NNLayer();

    void Calculate();

    void Backpropagate( std::vector< double >& dErr_wrt_dXn /* in */,
        std::vector< double >& dErr_wrt_dXnm1 /* out */,
        double etaLearningRate );

    NNLayer* m_pPrevLayer;
    VectorNeurons m_Neurons;
    VectorWeights m_Weights;
};

// Neuron class

class NNNeuron
{
public:
    NNNeuron( LPCTSTR str );
    virtual ~NNNeuron();

    void AddConnection( UINT iNeuron, UINT iWeight );
    void AddConnection( NNConnection const & conn );

    double output;

    VectorConnections m_Connections;
};

// Connection class

class NNConnection
{
public:
    NNConnection(UINT neuron = ULONG_MAX, UINT weight = ULONG_MAX);
    virtual ~NNConnection();

    UINT NeuronIndex;
    UINT WeightIndex;
};

// Weight class

class NNWeight
{
public:
    NNWeight( LPCTSTR str, double val = 0.0 );
    virtual ~NNWeight();

    double value;
};

类NeuralNetwork存储的是一个指针数组, 这些指针指向NN中的每一层, 即NNLayer. 没有专门的函数来增加层, 只需要使用std::vector::push_back()即可. NeuralNetwork类提供了两个基本的接口, 一个用来得到输出(Calculate), 一个用来训练(Backpropagete).

每一个NNLayer都保存一个指向前一层的指针, 使用这个指针可以获取上一层的输出作为输入. 另外它还保存了一个指针向量, 每个指针指向本层的神经元, 即NNNeuron, 当然, 还有连接的权值NNWeight. 和NeuralNetwork相似, 神经元和权值的增加都是通过std::vector::push_back()方法来执行的. NNLayer层还包含了函数Calculate()来计算神经元的输出, 以及Backpropagate()来训练它们. 实际上, NeuralNetwork类只是简单地调用每层的这些函数来实现上小节所说的2个同名方法.

每个NNNeuron保存了一个连接数组, 使用这个数组可以使得神经元能够获取输入. 使用NNNeuron::AddConnection()来增加一个Connection, 输入神经元的标号和权值的标号, 从而建立一个NNConnection对象, 并将它push_back()到神经元保存的连接数组中. 每个神经元同样保存着它自己的输出值(double). NNConnection和NNWeight类分别存储了一些信息.

你可能疑惑, 为何权值和连接要分开定义? 根据上述的原理, 每个连接都有一个权值, 为何不直接将它们放在一个类里?

原因是: 权值经常被连接共享.

实际上, 在卷积神经网络中就是共享连接的权值的. 所以, 举例来说, 就算一层可能有几百个神经元, 权值却可能只有几十个. 通过分离这两个概念, 这种共享可以很轻易地实现.

---

前向传递

前向传递是指所有的神经元基于接收的输入, 计算输出的过程.

在代码中, 这个过程通过调用NeuralNetwork::Calculate()来实现. NeuralNetwork::Calculate()直接设置输入层的神经元的值, 随后迭代剩下的层, 调用每一层的NNLayer::Calculate(). 这就是所谓的前向传递的串行实现方式. 串行计算并非是实现前向传递的唯一方法, 但它是最直接的. 下面是一个简化后的代码, 输入一个代表输入数据的C数组和一个代表输出数据的C数组.

// simplified code

void NeuralNetwork::Calculate(double* inputVector, UINT iCount,
               double* outputVector /* =NULL */,
               UINT oCount /* =0 */)

{
    VectorLayers::iterator lit = m_Layers.begin();
    VectorNeurons::iterator nit;

    // 第一层是输入层:
    // 直接设置所有的神经元输出为给定的输入向量即可

    if ( lit < m_Layers.end() )
    {
        nit = (*lit)->m_Neurons.begin();
        int count = ;

        ASSERT( iCount == (*lit)->m_Neurons.size() );
        // 输入和神经元个数应当一一对应

        while( ( nit < (*lit)->m_Neurons.end() ) && ( count < iCount ) )
        {
            (*nit)->output = inputVector[ count ];
            nit++;
            count++;
        }
    }

    // 调用Calculate()迭代剩余层

    for( lit++; lit<m_Layers.end(); lit++ )
    {
        (*lit)->Calculate();
    }

    // 使用结果设置每层输出

    if ( outputVector != NULL )
    {
        lit = m_Layers.end();
        lit--;

        nit = (*lit)->m_Neurons.begin();

        for ( int ii=; ii<oCount; ++ii )
        {
            outputVector[ ii ] = (*nit)->output;
            nit++;
        }
    }
}

在层中的Calculate()函数中, 层会迭代其中的所有神经元, 对于每一个神经元, 它的输出通过前馈公式给出: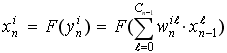 

这个公式通过迭代每个神经元的所有连接来实现, 获取对应的权重和对应的前一层神经元的输出. 如下:

// simplified code

void NNLayer::Calculate()
{
    ASSERT( m_pPrevLayer != NULL );

    VectorNeurons::iterator nit;
    VectorConnections::iterator cit;

    double dSum;

    for( nit=m_Neurons.begin(); nit<m_Neurons.end(); nit++ )
    {
        NNNeuron& n = *(*nit);  // 取引用

        cit = n.m_Connections.begin();

        ASSERT( (*cit).WeightIndex < m_Weights.size() );

        // 第一个权值是偏置
        // 需要忽略它的神经元下标

        dSum = m_Weights[ (*cit).WeightIndex ]->value;  

        for ( cit++ ; cit<n.m_Connections.end(); cit++ )
        {
            ASSERT( (*cit).WeightIndex < m_Weights.size() );
            ASSERT( (*cit).NeuronIndex <
                     m_pPrevLayer->m_Neurons.size() );

            dSum += ( m_Weights[ (*cit).WeightIndex ]->value ) *
                ( m_pPrevLayer->m_Neurons[
                   (*cit).NeuronIndex ]->output );
        }

        n.output = SIGMOID( dSum );

    }

}

SIGMOID是一个宏定义, 用于计算激励函数.

---

反向传播

BP是从最后一层向前移动的一个迭代过程. 假设在每一层我们都知道了它的输出误差. 如果我们知道输出误差, 那么修正权值来减少这个误差就不难. 问题是我们只能观测到最后一层的误差.

BP给出了一种通过当前层输出计算前一层的输出误差的方法. 它是一种迭代的过程: 从最后一层开始, 计算最后一层权值的修正, 然后计算前一层的输出误差, 反复.

BP的公式在下面. 代码中就用到了这个公式. 距离来说, 第一个公式告诉了我们如何去计算误差EP对于激励值yi的第n层的偏导数. 代码中, 这个变量名为dErr_wrt_dYn[ ii ].

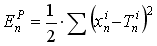
对于最后一层神经元的输出, 计算一个单输入图像模式的误差偏导的方法如下:

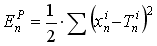(equation 1)

其中, 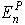是对于模式P再第n层的误差, 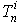是最后一层的期望输出, 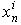是最后一层的实际输出.

给定上式, 我们可以得到偏导表达式:

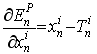(equation 2)

式2给出了BP过程的起始值. 我们使用这个数值作为式2的右值从而计算偏导的值. 使用偏导的值, 我们可以计算权值的修正量, 通过应用下式:

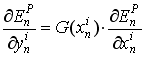(equation 3), 其中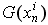是激励函数的导数.

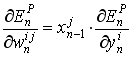(equation 4)

使用式2和式3, 我们可以计算前一层的误差, 使用下式5:

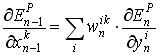(equation 5)

从式5中获取的值又可以立刻用作前一层的起始值. 这是BP的核心所在.

式4中获取的值告诉我们该如何去修正权值, 按照下式:

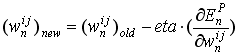(equation 6)

其中eta是学习速率, 常用值是0.0005, 并随着训练减小.

本代码中, 上述等式在NeuralNetwork::Backpropagate()中实现. 输入实际上是神经网络的实际输出和期望输出. 使用这两个输入, NeuralNetwork::Backpropagate()计算式2的值并迭代所有的层, 从最后一层一直迭代到第一层. 对于每层, 都调用了NNLayer::Backpropagate(). 输入是梯度值, 输出则是式5.

这些梯度都保存在一个两维数组differentials中.

本层的输出则作为前一层的输入.

// simplified code
void NeuralNetwork::Backpropagate(double *actualOutput,
     double *desiredOutput, UINT count)
{
    // 神经网络的BP过程,
    // 从最后一层迭代向前处理到第一层为止.
    // 首先, 单独计算最后一层,
    // 因为它提供了前一层所需的梯度信息
    // (i.e., dErr_wrt_dXnm1)

    // 变量含义:
    //
    // Err - 整个NN的输出误差
    // Xn - 第n层的输出向量
    // Xnm1 - 前一层的输出向量
    // Wn - 第n层的权值向量
    // Yn - 第n层的激励函数输入值
    // 即, 在应用压缩函数(squashing function)前的权值和// F - 挤压函数: Xn = F(Yn)
    // F' - 压缩函数(squashing function)的梯度
    //   比如, 令 F = tanh,
    //   则 F'(Yn) = 1 - Xn^2, 梯度可以通过输出来计算, 不需要输入信息

    VectorLayers::iterator lit = m_Layers.end() - ; // 取最后一层

    std::vector< double > dErr_wrt_dXlast( (*lit)->m_Neurons.size() ); // 记录后层神经元误差对输入的梯度
    std::vector< std::vector< double > > differentials; //记录每一层输出对输入的梯度

    int iSize = m_Layers.size(); // 层数

    differentials.resize( iSize ); 

    int ii;

    // 计算最后一层的 dErr_wrt_dXn 来开始整个迭代.
    // 对于标准的MSE方程
    // (比如, 0.5*sumof( (actual-target)^2 ),
    // 梯度表达式就仅仅是期望和实际的差: Xn - Tn

    for ( ii=; ii<(*lit)->m_Neurons.size(); ++ii )
    {
        dErr_wrt_dXlast[ ii ] =
            actualOutput[ ii ] - desiredOutput[ ii ];
    }

    // 保存 Xlast 并分配内存存储剩余的梯度

    differentials[ iSize- ] = dErr_wrt_dXlast;  // 最后一层的梯度

    for ( ii=; ii<iSize-; ++ii )
    {
        differentials[ ii ].resize(
             m_Layers[ii]->m_Neurons.size(), 0.0 );
    }

    // 迭代每个层, 包括最后一层但不包括第一层
    // 同时求得每层的BP误差并矫正权值// 返回梯度dErr_wrt_dXnm1用于下一次迭代

    ii = iSize - ;
    for ( lit; lit>m_Layers.begin(); lit--)
    {
        (*lit)->Backpropagate( differentials[ ii ],
              differentials[ ii -  ], m_etaLearningRate ); // 调用每一层的BP接口
        --ii;
    }

    differentials.clear();
}

在NNLayer::Backpropagate()中, 层实现了式3~5, 计算出了梯度. 实现了式6来更新本层的权重. 在下面的代码中, 激励函数的梯度被定义为 DSIGMOID.

// simplified code

void NNLayer::Backpropagate( std::vector< double >& dErr_wrt_dXn /* in */,
                            std::vector< double >& dErr_wrt_dXnm1 /* out */,
                            double etaLearningRate )
{
    double output;

    // 计算式 (3): dErr_wrt_dYn = F'(Yn) * dErr_wrt_Xn

    for ( ii=; ii<m_Neurons.size(); ++ii ) // 遍历所有神经元
    {
        output = m_Neurons[ ii ]->output; // 神经元输出

        dErr_wrt_dYn[ ii ] = DSIGMOID( output ) * dErr_wrt_dXn[ ii ]; // 误差对输入的梯度
    }

    // 计算式 (4): dErr_wrt_Wn = Xnm1 * dErr_wrt_Yn
    // 对于本层的每个神经元, 遍历前一层的连接
    // 更新对应权值的梯度

    ii = ;
    for ( nit=m_Neurons.begin(); nit<m_Neurons.end(); nit++ ) // 迭代本层所有神经元
    {
        NNNeuron& n = *(*nit);  // 取引用

        for ( cit=n.m_Connections.begin(); cit<n.m_Connections.end(); cit++ ) // 遍历每个神经元的后向连接
        {
            kk = (*cit).NeuronIndex; // 连接的前一层神经元标号
            if ( kk == ULONG_MAX ) // 偏置的标号固定为最大整形量
            {
                output = 1.0;  // 偏置
            }
            else // 其他情况下 神经元输出等于前一层对应神经元的输出 Xn-1
            {
                output = m_pPrevLayer->m_Neurons[ kk ]->output;
            }
            // 误差对权值的梯度
　          // 每次使用对应神经元的误差对输入的梯度
            dErr_wrt_dWn[ (*cit).WeightIndex ] += dErr_wrt_dYn[ ii ] * output;
        }

        ii++;
    }

    // 计算式 (5): dErr_wrt_Xnm1 = Wn * dErr_wrt_dYn,// 需要dErr_wrt_Xn的值来进行前一层的BP

    ii = ;
    for ( nit=m_Neurons.begin(); nit<m_Neurons.end(); nit++ ) // 迭代所有神经元
    {
        NNNeuron& n = *(*nit);  // 取引用

        for ( cit=n.m_Connections.begin();
              cit<n.m_Connections.end(); cit++ ) // 遍历每个神经元所有连接
        {
            kk=(*cit).NeuronIndex;
            if ( kk != ULONG_MAX )
            {
                // 排除了ULONG_MAX, 提高了偏置神经元的重要性// 因为我们不能够训练偏置神经元

                nIndex = kk;

                dErr_wrt_dXnm1[ nIndex ] += dErr_wrt_dYn[ ii ] *
                       m_Weights[ (*cit).WeightIndex ]->value;
            }

        }

        ii++;  // ii 跟踪神经元下标

    }

    // 计算式 (6): 更新权值
    // 在本层使用 dErr_wrt_dW (式4)
    // 以及训练速率eta

    for ( jj=; jj<m_Weights.size(); ++jj )
    {
        oldValue = m_Weights[ jj ]->value;
        newValue = oldValue.dd - etaLearningRate * dErr_wrt_dWn[ jj ];
        m_Weights[ jj ]->value = newValue;
    }
}