最长上升子序列(LIS)n2 nlogn算法解析

题目描述

给定一个数列，包含N个整数，求这个序列的最长上升子序列。

例如 2 5 3 4 1 7 6 最长上升子序列为 4.

1.O(n²)算法解析

看到这个题，大家的直觉肯定都是要用动态规划来做，那么我们先设立一个数组。

设d[ i ]为以a[ i ]为结尾的最大子序列的长度

有了这个后，我们可以很容易的写出状态转移方程：

d[ i ] = max(d[ i ] , d[ j ] + 1) 若 j < i 且 a[ i ] > a[ j ]

#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;
#define N 1000
int d[N];//表示以a[i]结尾的最大长度
int a[N];
int main() {
	for (int i = 0; i < 7; i++) {
		cin >> a[i];
	}
	d[0] = 1;
	for (int i = 1; i < 7; i++) {
		d[i] = 1;
		for (int j = 0; j < i; j++) {
			if (a[i] > a[j])
				d[i] = max(d[j] + 1, d[i]);
		}
	}
	int maxt = -1;
	for (int i = 0; i < 7; i++) {
		maxt = max(d[i], maxt);
	}
	cout << maxt << endl;
	return 0;
}

2.O(ologn)算法解析

首先我们给数组d换一种含义，设d[ i ] 为 长度为 i 的子序列的最后一个元素的值。

我们要做的就是，依次把每一个元素插到他合适的位置上去。

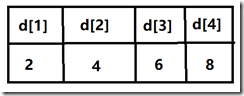
例如现在的数组d为

这时我们要处理一个元素，假设值为5，那我们应该放到哪里？

这里面长度为2的子序列最后一个长度为4，5>4，因此我们可以把5放到d[3]中。

但是把6换成5有什么意义呢？

显然，序列元素有限的情况下，子序列的末尾元素越小，越有利于我们向后添加元素（增大其长度）。

这句话就是解决问题的关键。

因此，处理每一个元素的时候，我们只需要把元素填入第一个大于这个元素值的d[ i ]中就好。

通过简单的分析，我们很容易知道数组d是个递增的数组，因此解决上面这个问题，我们采用二分查找，写一个find()函数，返回第一个大于该元素值 t 的数组d元素的下标。

#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;
#define N 1000
int d[N];
int a[N];
int find(int l, int r, int x) {//寻找数组d中第一个大于x的元素的下标
	while (l <= r) {
		int mid = (l + r) / 2;
		if (d[mid] < x) {
			l = mid + 1;
		}
		else {
			r = mid - 1;
		}
	}
	return l;
}
int main() {
	for (int i = 0; i < 7; i++) {
		cin >> a[i];
	}
	d[0] = -0x3f3f3f3f;
	int len = 1;
	for (int i = 1; i < 7; i++) {
		if (a[i] > d[len]) {
			d[++len] = a[i];
		}
		else {
			int k = find(1, len, a[i]);
			d[k] = a[i];
		}
	}
	cout << len;
	return 0;
}