HDU 1710 Binary Tree Traversals（树的建立，前序中序后序）

Binary Tree Traversals

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 9283    Accepted Submission(s):
4193

Problem Description

A binary tree is a finite set of vertices that is
either empty or consists of a root r and two disjoint binary trees called the
left and right subtrees. There are three most important ways in which the
vertices of a binary tree can be systematically traversed or ordered. They are
preorder, inorder and postorder. Let T be a binary tree with root r and subtrees
T1,T2.

In a preorder traversal of the vertices of T, we visit the root r
followed by visiting the vertices of T1 in preorder, then the vertices of T2 in
preorder.

In an inorder traversal of the vertices of T, we visit the
vertices of T1 in inorder, then the root r, followed by the vertices of T2 in
inorder.

In a postorder traversal of the vertices of T, we visit the
vertices of T1 in postorder, then the vertices of T2 in postorder and finally we
visit r.

Now you are given the preorder sequence and inorder sequence of
a certain binary tree. Try to find out its postorder sequence.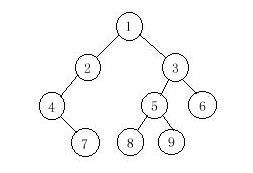

 

Input

The input contains several test cases. The first line
of each test case contains a single integer n (1<=n<=1000), the number of
vertices of the binary tree. Followed by two lines, respectively indicating the
preorder sequence and inorder sequence. You can assume they are always
correspond to a exclusive binary tree.

 

Output

For each test case print a single line specifying the
corresponding postorder sequence.

 

Sample Input

9
1 2 4 7 3 5 8 9 6
4 7 2 1 8 5 9 3 6

 

Sample Output

7 4 2 8 9 5 6 3 1

 

Source

HDU
2007-Spring Programming Contest

 

Recommend

lcy   |   We have carefully selected several similar
problems for you:  1708 1707 1709 1509 1512 

 

总结：记录下根结点，再拆分左右子树，一直搜下去。

 #include<iostream>
 #include <cstring>
 #include <string>
 #include <algorithm>
 using namespace std;
 
 typedef struct tree
 {
     int v;
     tree *l, *r;
 };
 tree *root;
 
 tree *build(int *a, int *b, int n)//函数不能少了*
 {
     tree *s;
     int i;
     for (i = ; i <= n; i++)
     {
         if (a[] == b[i])
         {
             s = (tree*)malloc(sizeof(tree));//开辟空间
             s->v = b[i];
             s->l = build(a+, b, i-);
             s->r = build(a + i, b + i, n - i );
             return s;//要记得返回
         }
     }
     return NULL;
 }
 
 void postorder(tree *ro)
 {
     if (ro == NULL) return;
     postorder(ro->l);
     postorder(ro->r);
     if (ro == root)
     {
         printf("%d\n", ro->v);
     }
     else
     {
         printf("%d ", ro->v);
     }
 }
 
 int main()
 {
     int n, a[], b[];
     while (cin>>n)
     {
         int i;
         for (i = ; i <=n; i++)
         {
             cin >> a[i];
         }
         for (i = ; i <= n; i++)
         {
             cin >> b[i];
         }
         root = build(a, b, n);
         postorder(root);
     }
     return ;
 }

另一种不建树的方法

 #include <iostream>
 #include <cstring>
 #include <algorithm>
 #define maxn 1111
 int n, pre[maxn], in[maxn], post[maxn], id[maxn], res;//pre表示前序遍历序列,in表示中序遍历序列
 void print(int a, int b, int c, int d)//a,b,c,d分别表示前序和中序遍历序列的起点和终点
 {
     int i = id[pre[a]];//根节点
     int j = i - c;//中序遍历序列的左子树
     int k = d - i;//中序遍历序列的右子树
     if (j) print(a + , a + j, c, i - );//左子树非空则递归左子树
     if (k) print(a + j + , b, i + , d);//右子树非空则递归右子树
     post[res++] = pre[a];
 }
 int main()
 {
     while (~scanf("%d", &n))
     {
         res = ;
         for (int i = ; i<n; i++) scanf("%d", &pre[i]);
         for (int i = ; i<n; i++) scanf("%d", &in[i]), id[in[i]] = i;
         print(, n - , , n - );
         for (int i = ; i<n; i++)
             printf("%d%c", post[i], i == n -  ? '\n' : ' ');
     }
     return ;
 }

 #include <stdio.h>
 
 static int pre[];
 static int mid[];
 
 /**
 每次处理数组中的一个小块
 特点：先序和后序遍历任意子树都是连续的块
 **/
 void post(int pre_index, int mid_index, int size, int is_root)
 {
     if (!size) {
         return;
     }
 
     if (size == )
     {
         //打印先序
         printf("%d ", pre[pre_index]);
         return;
     }
 
     //每个（子）树根的位置
     int root;
 
     //找到根节点
     for (root = ; root < size && pre[pre_index] !=
         mid[mid_index + root]; root++);
 
     //处理根的左边
     post(pre_index + , mid_index, root, );
     //处理根的右边
     post(pre_index + root + , mid_index + root + ,
         size - root - , );
     //是否是总根，打印根（相对）
     is_root ? printf("%d\n", pre[pre_index]) :
         printf("%d ", pre[pre_index]);
 }
 
 int main()
 {
     int n, i;
     n = ;
     while (~scanf("%d", &n))
     {
         for (i = ; i < n; i++)
             scanf("%d", &pre[i]);
         for (i = ; i < n; i++)
             scanf("%d", &mid[i]);
         post(, , n, );
     }
     return ;
 }