《啊哈算法》中P81解救小哈

题目描述

首先我们用一个二维数组来存储这个迷宫，刚开始的时候，小哼处于迷宫的入口处（1,1），小哈在（p,q）。其实这道题的的本质就在于找从（1,1）到（p,q）的最短路径。

此时摆在小哼面前的路有两条，我们可以先让小哼往右边走，直到走不通的时候再回到这里，再去尝试另外一个方向。

在这里我们规定一个顺序，按照顺时针的方向来尝试（即右→下→左→上）。

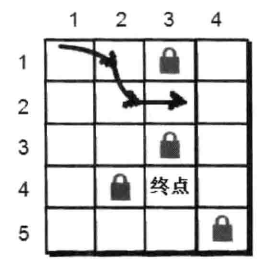
我们先来看看小哼一步之内可以到达的点有哪些？只有（1,2）和（2,1）。

根据刚才的策略，我们先往右边走，但右边（1,3）有障碍物，所以只能往下（2,2）这个点走。但是小哈并不在（2,2）这个点上，所以小哼还得继续往下走，直至无路可走或者找到小哈为止。

注意：并不是让我们找到小哈此题就解决了。因为刚才只是尝试了一条路的走法，而这条路并不一定是最短的。刚才很多地方在选择方向的时候都有多种选择，因此我们需要返回到这些地方继续尝试往别的方向走，直到把所有可能都尝试一遍，最后输出最短的一条路径。

例如下图就是一条可行的搜索路径：

dfs

#include<stdio.h>
int n,m,p,q,min=99999999;
int a[51][51],book[51][51];
void dfs(int x,int y,int step)
{
    int next[4][2]={
    {0,1},//向右走
    {1,0},//向下走
    {0,-1},//向左走
    {-1,0},//向上走
    };
    int tx,ty,k;
    if(x==p && y==p)  //判断是否到达小哈的位置
    {
        if(step<min)
            min=step;  //更新最小值
        return;
    }
    /*枚举四种走法*/
    for(k=0;k<=3;k++)
    {
        /*计算下一个点的坐标*/
        tx=x+next[k][0];
        ty=y+next[k][1];
        if(tx<1 || tx>n || ty<1 || ty>m)  //判断是否越界
            continue;
        /*判断该点是否为障碍物或者已经在路径中*/
        if(a[tx][ty]==0 && book[tx][ty]==0)
        {
            book[tx][ty]=1;  //标记这个点已经走过
            dfs(tx,ty,step+1);  //开始尝试下一个点
            book[tx][ty]=0;  //尝试结束，取消这个点的标记
        }
    }
    return;
} 

int main()
{
    int i,j,startx,starty;
    scanf("%d %d",&n,&m);  //读入n和m，n为行，m为列
    /*读入迷宫*/
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    scanf("%d %d %d %d",&startx,&starty,&p,&q);  //读入起点和终点坐标
    /*从起点开始搜索*/
    book[startx][starty]=1;  //标记起点已经在路径中，防止后面重复走
    dfs(startx,starty,0);  //第一个参数是起点的x坐标，以此类推是起点的y坐标，初始步数为0
    printf("%d",min);  //输出最短步数
    return 0;
}

bfs

#include<stdio.h>
struct note{
	int x;  //横坐标
	int y;  //纵坐标
	int f;  //父亲在队列中的编号（本题不需要输出路径，可以不需要f）
	int s;  //步数
};
int main()
{
	struct note que[2501];  //因为地图大小不超过50*50，因此队列扩展不会超过2500个

	int a[51][51] = {0};  //用来存储地图
	int book[51][51] = {0};  //数组book的作用是记录哪些点已经在队列中了，防止一个点被重复扩展，并全部初始化为0
	//定义一个用于表示走的方向的数组
	int next[4][2] = {  //顺时针方向
	{0,1}, //向右走
	{1,0},  //向下走
	{0,-1},  //向左走
	{-1,0},  //向上走
	};

	int head,tail;
	int i,j,k,n,m,startx,starty,p,q,tx,ty,flag;

	scanf("%d %d",&n,&m);
	for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
			scanf("%d",&a[i][j]);
	scanf("%d %d %d %d",&startx,&starty,&p,&q);

	//队列初始化
	head = 1;
	tail = 1;
	//往队列插入迷宫入口坐标
	que[tail].x = startx;
	que[tail].y = starty;
	que[tail].f = 0;
	que[tail].s = 0;
	tail++;
	book[startx][starty] = 1;

	flag = 0;  //用来标记是否到达目标点，0表示暂时没有到达， 1表示已到达
	while(head < tail){  //当队列不为空时循环
		for(k=0;k<=3;k++)  //枚举四个方向
		{
			//计算下一个点的坐标
			tx = que[head].x + next[k][0];
			ty = que[head].y + next[k][1];
			if(tx < 1 || tx > n || ty < 1 || ty > m)  //判断是否越界
				continue;
			if(a[tx][ty] == 0 && book[tx][ty] == 0)  //判断是否是障碍物或者已经在路径中
				{
					book[tx][ty] = 1;  //把这个点标记为已经走过。注意bfs每个点通常情况下只入队一次，和深搜不同，不需要将book数组还原
					//插入新的点到队列中
					que[tail].x = tx;
					que[tail].y = ty;
					que[tail].f = head;  //因为这个点是从head扩展出来的，所以它的父亲是head，本题不需要求路径，因此可省略
					que[tail].s = que[head].s+1;  //步数是父亲的步数+1
					tail++; 

				}
			if(tx == p && ty == q)  //如果到目标点了，停止扩展，任务结束，退出循环
			{
				flag = 1;  //重要！两句不要写反
				break;
			}
		}
		if(flag == 1)
			break;
		head++;  //当一个点扩展结束后，才能对后面的点再进行扩展
	}
	printf("%d",que[tail-1].s);  //打印队列中末尾最后一个点，也就是目标点的步数
 	//注意tail是指向队列队尾（最后一位）的下一个位置，所以这里需要减1
	getchar();getchar();
	return 0;
}