POJ1113:Wall (凸包：求最小的多边形，到所有点的距离大于大于L)

Once upon a time there was a greedy King who ordered his chief Architect to build a wall around the King's castle. The King was so greedy, that he would not listen to his Architect's proposals to build a beautiful brick wall with a perfect shape and nice tall towers. Instead, he ordered to build the wall around the whole castle using the least amount of stone and labor, but demanded that the wall should not come closer to the castle than a certain distance. If the King finds that the Architect has used more resources to build the wall than it was absolutely necessary to satisfy those requirements, then the Architect will loose his head. Moreover, he demanded Architect to introduce at once a plan of the wall listing the exact amount of resources that are needed to build the wall. 

Your task is to help poor Architect to save his head, by writing a program that will find the minimum possible length of the wall that he could build around the castle to satisfy King's requirements.

The task is somewhat simplified by the fact, that the King's castle has a polygonal shape and is situated on a flat ground. The Architect has already established a Cartesian coordinate system and has precisely measured the coordinates of all castle's vertices in feet.

Input

The first line of the input file contains two integer numbers N and L separated by a space. N (3 <= N <= 1000) is the number of vertices in the King's castle, and L (1 <= L <= 1000) is the minimal number of feet that King allows for the wall to come close to the castle.

Next N lines describe coordinates of castle's vertices in a clockwise order. Each line contains two integer numbers Xi and Yi separated by a space (-10000 <= Xi, Yi <= 10000) that represent the coordinates of ith vertex. All vertices are different and the sides of the castle do not intersect anywhere except for vertices.

Output

Write to the output file the single number that represents the minimal possible length of the wall in feet that could be built around the castle to satisfy King's requirements. You must present the integer number of feet to the King, because the floating numbers are not invented yet. However, you must round the result in such a way, that it is accurate to 8 inches (1 foot is equal to 12 inches), since the King will not tolerate larger error in the estimates.

Sample Input

9 100
200 400
300 400
300 300
400 300
400 400
500 400
500 200
350 200
200 200

Sample Output

1628

Hint

结果四舍五入就可以了

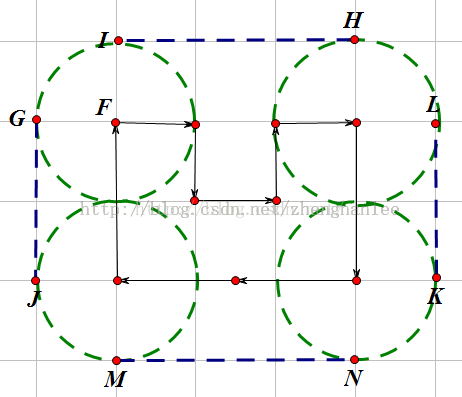
题意：给定N个点，求用一个多边形把这些点包括进去，且每个点到多边形的距离都大于等于L。

思路：

先不考虑L这个条件，因为两点之间，直线最短，所以对于凹进去的部分，我们肯定有最短的直线可以包含它，可以忽略，所以是求凸包。

然后考虑L，对于求出的凸多边形，对于它的顶点X，可以证明每个X附近需要增加一定的圆弧来保证顶点到圆弧的距离大于等于L，

所有X的圆弧角度之和为Pi，将凸包平移与圆弧连接成封闭图案，最终 ans=凸包+2*Pi*L。

看图就知道了--->

Graham算法求凸包：

（注意需要对N讨论，此题N>=3，所以没有讨论）。

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=;
const double pi=acos(-1.0);
const double eps=1e-;
struct Cpoint
{
    double x,y;
    Cpoint(){}
    Cpoint(double xx,double yy):x(xx),y(yy){}
    Cpoint friend operator -(Cpoint a,Cpoint b){
        return Cpoint(a.x-b.x, a.y-b.y);
    }
    double friend operator ^(Cpoint a,Cpoint b){
        return a.x*b.y-b.x*a.y;
    }
    bool friend operator <(Cpoint a,Cpoint b){
        if(a.y==b.y) return a.x<b.x;
        return a.y<b.y;
    }
};
double dist(Cpoint a,Cpoint b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
int Sign(double x)
{
    if(x>=-eps&&x<=eps) return ;
    if(x>eps) return ; return -;
}
int N,L; Cpoint P[maxn];
bool cmp(Cpoint a,Cpoint b)
{
    int s=Sign((a-P[])^(b-P[]));
    if(s>||(s==&&dist(a,P[])<dist(b,P[]))) return true;
    return false;
}
double Graham()  //如果N<3还得讨论一下。
{
    double res=;
    sort(P+,P+N+); //得到“原点 ”
    sort(P+,P+N+,cmp);  //得到积角序
    int q[maxn],top=;
    q[]=; q[]=; q[]=;
    for(int i=;i<=N;i++){
        while(top>&&Sign((P[q[top]]-P[q[top-]])^(P[i]-P[q[top]]))<=) top--;
        q[++top]=i;
    }
    for(int i=;i<top;i++) res+=dist(P[q[i]],P[q[i+]]);
    res=res+dist(P[q[top]],P[])+2.0*pi*L;
    return res;
}
int main()
{
    while(~scanf("%d%d",&N,&L)){
        for(int i=;i<=N;i++)
            scanf("%lf%lf",&P[i].x,&P[i].y);
        printf("%d\n",(int)(Graham()+0.5));
    }return ;
}