BZOJ 3309 DZY Loves Math ——莫比乌斯反演

枚举$d=gcd(i,j)$

然后大力反演

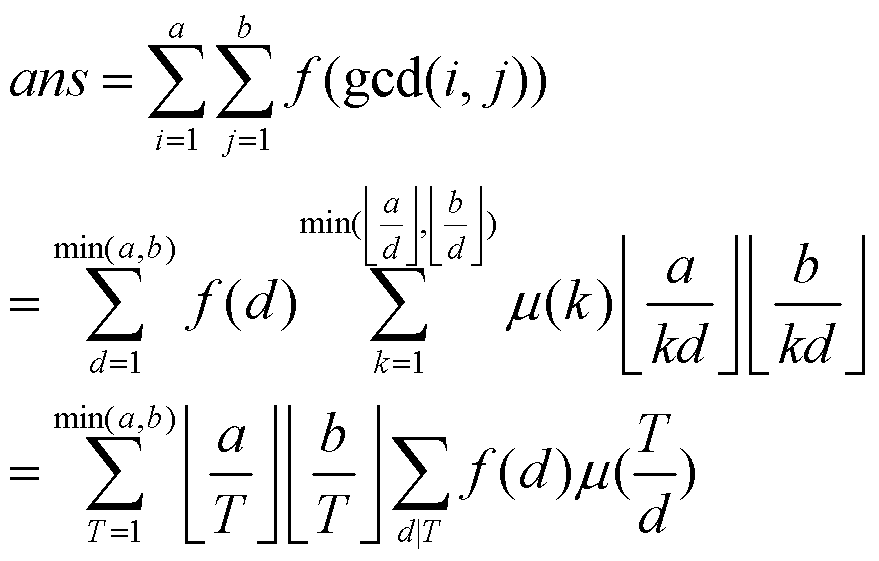——来自Popoqqq的博客。

然后大力讨论后面的函数的意义即可。

http://blog.csdn.net/popoqqq/article/details/42122413

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define F(i,j,k) for (int i=j;i<=k;++i)
#define D(i,j,k) for (int i=j;i>=k;--i)
#define ll long long
#define maxn 10000005
#define inf 0x3f3f3f3f
 
int g[maxn],pr[maxn],top,a[maxn],b[maxn];
bool vis[maxn];
 
void init()
{
    memset(vis,false,sizeof vis);
    F(i,2,maxn-1)
    {
        if (!vis[i])
        {
            pr[++top]=i;
            g[i]=1;
            a[i]=1;
            b[i]=i;
        }
        F(j,1,top)
        {
            if ((ll)i*pr[j]>=maxn) break;
            vis[i*pr[j]]=true;
            if (i%pr[j]==0)
            {
                a[i*pr[j]]=a[i]+1;
                b[i*pr[j]]=b[i]*pr[j];
                int tmp=i/b[i];
                if (tmp==1) g[i*pr[j]]=1;
                else g[i*pr[j]]=(a[tmp]==a[i*pr[j]])?-g[tmp]:0;
                break;
            }
            a[i*pr[j]]=1;
            b[i*pr[j]]=pr[j];
            g[i*pr[j]]=(a[i]==1?-g[i]:0);
        }
    }
    F(i,2,maxn-1) g[i]=g[i-1]+g[i];
}
 
int t,n,m;
 
int main()
{
    init();
    scanf("%d",&t);
    while (t--)
    {
        scanf("%d%d",&n,&m);ll ans=0;
        if (n>m) n^=m^=n^=m;
        for (int i=1,last=0;i<=n;i=last+1)
        {
            last=min(n/(n/i),m/(m/i));
            ans+=((ll)g[last]-g[i-1])*(n/i)*(m/i);
        }
        printf("%lld\n",ans);
    }
}