SKU多维属性状态判断算法

作者：周琪力，前端工程师，网络常用昵称「keelii」。在过去的4年里主要负责京东网站商品详情页的前端系统架构和开发，平时主要写 JavaScript 偶尔写点NodeJS，Python。琪力博客： https://keelii.github.io/。

问题描述

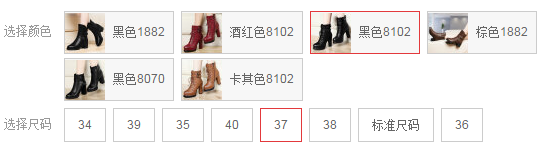
这个问题来源于选择商品属性的场景。比如我们买衣服、鞋子这类物件，一般都需要我们选择合适的颜色、尺码等属性

先了解一下 SKU的学术概念吧

最小库存管理单元（Stock Keeping Unit, SKU）是一个会计学名词，定义为库存管理中的最小可用单元，例如纺织品中一个SKU通常表示规格、颜色、款式，而在连锁零售门店中有时称单品为一个SKU。最小库存管理单元可以区分不同商品销售的最小单元，是科学管理商品的采购、销售、物流和财务管理以及POS和MIS系统的数据统计的需求，通常对应一个管理信息系统的编码。 —— form wikipedia 最小存货单位

简单的结合上面的实例来说： SKU就是你上购物网站买到的最终商品，对应的上图中已选择的属性是：颜色黑色 - 尺码 37。

我先看看后端数据结构一般是这样的，一个线性数组，每个元素是一个描述当前SKU的Map，比如：

[

   { "颜色": "红", "尺码": "大", "型号": "A", "skuId": "3158054" },

   { "颜色": "白", "尺码": "中", "型号": "B", "skuId": "3133859" },

   { "颜色": "蓝", "尺码": "小", "型号": "C", "skuId": "3516833" }

]

前端展示的时候显然需要 group 一下，按不同的属性分组，目的就是让用户按属性的维度去选择，group 后的数据大概是这样的：

{    
"颜色": ["红", "白", "蓝"],    
"尺码": ["大", "中", "小"],    
"型号": ["A", "B", "C"]

}

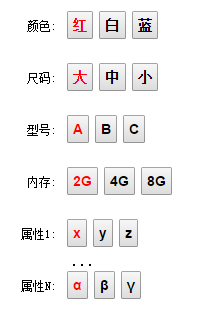
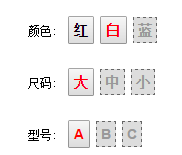
对应的在网页上大概是这样的 UI

这个时候，就会有一个问题，这些元子属性能组成的集合（用户的选择路径）远远大于真正可以组成的集合，比如上面的属性集合可以组合成一个笛卡尔积，即。可以组合成以下序列：

[

    ["红", "大", "A"],    // ✔

    ["红", "大", "B"],

    ["红", "大", "C"],

    ["红", "中", "A"],

    ["红", "中", "B"],

    ["红", "中", "C"],

    ["红", "小", "A"],

    ["红", "小", "B"],

    ["红", "小", "C"],

    ["白", "大", "A"],

    ["白", "大", "B"],

    ["白", "大", "C"],

    ["白", "中", "A"],

    ["白", "中", "B"],    // ✔

    ["白", "中", "C"],

    ["白", "小", "A"],

    ["白", "小", "B"],

    ["白", "小", "C"],

    ["蓝", "大", "A"],

    ["蓝", "大", "B"],

    ["蓝", "大", "C"],

    ["蓝", "中", "A"],

    ["蓝", "中", "B"],

    ["蓝", "中", "C"],

    ["蓝", "小", "A"],

    ["蓝", "小", "B"],

    ["蓝", "小", "C"]     // ✔]

根据公式可以知道，一个由 3 个元素，每个元素是有 3 个元素的子集构成的集合，能组成的笛卡尔积一共有 3 的 3 次幂，也就是 27 种，然而源数据只可以形成 3 种组合。

这种情况下最好能提前判断出来不可选的路径并置灰，告诉用户，否则会造成误解。

确定规则

看下图，如果我们定义红色为当前选中的商品的属性，即当前选中商品为红-大-A，这个时候如何确认其它非已选属性是否可以组成可选路径？

规则是这样的：假设当前用户想选白-大-A，刚好这个选择路径是不存在的，那么我们就把白置灰。

以此类推，如果要确认蓝属性是否可用，需要查找蓝-大-A 路径是否存在

…

解决方法

根据上面的逻辑代码实现思路就有了：

1. 遍历所有非已选元素：”白”, “蓝”, “中”, “小”, “B”, “C”

遍历所有属性行： ”颜色”, “尺码”, “型号”

取： a) 当前元素 b) 非当前元素所在的其它属性已选元素，形成一个路径

判断此路径是否存在，如果不存在将当前元素置灰

看来问题似乎已经解决了，然而 …

我们忽略了一个非常重要的问题：上例中虽然白元素置灰，但是实际上白是可以被点击的！因为用户可以选择白-中-B 路径。

如果用户点击了白情况就变得复杂了很多，我们假设用户只选择了一个元素白，此时如何判断其它未选元素是否可选？

即：如何确定 ”大”, “中”, “小”, “A”, “B”, “C” 需要置灰？注意我们并不需要确认 “红”，“蓝”是否可选，因为属性里面的元素都是单选，当前的属性里任何元素都可选的。

缩小问题规模

我们先缩小问题范围：当前情况下（只有一个白已选）如何确定尺码 “大” 需要置灰？你可能会想到根据我们之间的逻辑，需要分别查找：

白 - 大 - A
白 - 大 - B
白 - 大 - C

他们都不存在的时候把尺码大置灰，问题似乎也可以解决。其实这样是不对的，因为型号没有被选择过，所以只需要知道白-大是否可选即可。

同时还有一个问题，如果已选的个数不确定而且维度可以增加到不确定呢？

这种情况下如果还按之前的算法，即使实现也非常复杂。这时候就要考虑换一种思维方式。

调整思路

之前我们都是反向思考，找出不可选应该置灰的元素。我们现在正向的考虑，如何确定属性是否可选。而且多维的情况下用户可以跳着选。比如：用户选了两个元素白，B

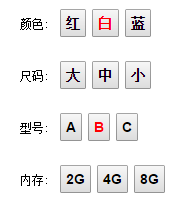图1

我们再回过头来看下原始存在的数据

[

   { "颜色": "红", "尺码": "大", "型号": "A", "skuId": "3158054" },

   { "颜色": "白", "尺码": "中", "型号": "B", "skuId": "3133859" },

   { "颜色": "蓝", "尺码": "小", "型号": "C", "skuId": "3516833" }

]

即
[

   [ "红", "大", "A" ],   // 存在

   [ "白", "中", "B" ],   // 存在

   [ "蓝", "小", "C" ]    // 存在
]

显然：如果第一条数据 “红”, “大”, “A” 存在，那么下面这些子组合肯定都存在：

红
大
A
红 - 大
红 - A
大 - A
红 - 大 - A

同理：如果第二条数据 ”白”, “中”, “B” 存在，那么下面这些子组合肯定都存在：

白
中
B
白 - 中
白 - B
中 - B
白 - 中 - B

…

我们提前把所有存在的路径中的子组合算出来，算法上叫取集合所有子集，数学上叫幂集，形成一个所有存在的路径表，算法如下：

/**

 * 取得集合的所有子集「幂集」

 arr = [1,2,3]

   i = 0, ps = [[]]:

     j = 0; j < ps.length => j < 1:

         i=0, j=0 ps.push(ps[0].concat(arr[0])) => ps.push([].concat(1)) => [1]

              ps = [[], [1]]

   i = 1, ps = [[], [1]] :

     j = 0; j < ps.length => j < 2

         i=1, j=0 ps.push(ps[0].concat(arr[1])) => ps.push([].concat(2))  => [2]

         i=1, j=1 ps.push(ps[1].concat(arr[1])) => ps.push([1].concat(2)) => [1,2]

              ps = [[], [1], [2], [1,2]]

   i = 2, ps = [[], [1], [2], [1,2]]

     j = 0; j < ps.length => j < 4

         i=2, j=0 ps.push(ps[0].concat(arr[2])) => ps.push([3])    => [3]

         i=2, j=1 ps.push(ps[1].concat(arr[2])) => ps.push([1, 3]) => [1, 3]

         i=2, j=2 ps.push(ps[2].concat(arr[2])) => ps.push([2, 3]) => [2, 3]

         i=2, j=3 ps.push(ps[3].concat(arr[2])) => ps.push([2, 3]) => [1, 2, 3]

              ps = [[], [1], [2], [1,2], [3], [1, 3], [2, 3], [1, 2, 3]]

 */

function powerset(arr) {    
  var ps = [[]];    
  for (var i=0; i < arr.length; i++) {  
    for (var j = 0, len = ps.length; j < len; j++) {

     ps.push(ps[j].concat(arr[i]));

    }

  }
  return ps;

}

有了这个存在的子集集合，再回头看图1 举例：

图1

如何确定红可选？只需要确定红-B 可选
如何确定中可选？需要确定白-中-B 可选
如何确定 2G 可选？需要确定白-B-2G 可选

算法描述如下：

遍历所有非已选元素

a. 遍历所有属性行

取： a) 当前元素 b) 非当前元素所在的其它属性已选元素（如果当前属性中没已选元素，则跳过），形成一个路径

判断此路径是否存在（在所有存在的路径表中查询），如果不存在将当前元素置灰

以最开始的后端数据为例，生成的所有可选路径表如下：注意路径用分割符号「-」分开是为了查找路径时方便，不用遍历

{
    "": {
            "skus": ["3158054", "3133859", "3516833"]

    },
    "红": {
            "skus": ["3158054"]

    },    
    "大": {
            "skus": ["3158054"]

    },    
    "红-大": {
            "skus": ["3158054"]

    },    
    "A": {
            "skus": ["3158054"]

    },    
    "红-A": {
            "skus": ["3158054"]

    },    
    "大-A": {
            "skus": ["3158054"]

    },    
    "红-大-A": {
            "skus": ["3158054"]

    },    
    "白": {
            "skus": ["3133859"]

    },    
    "中": {
            "skus": ["3133859"]

    },    
    "白-中": {
            "skus": ["3133859"]

    },    
    "B": {
            "skus": ["3133859"]

    },
    "白-B": {
            "skus": ["3133859"]

    },
    "中-B": {
            "skus": ["3133859"]

    },    
    "白-中-B": {
            "skus": ["3133859"]

    },    
    "蓝": {
            "skus": ["3516833"]

    },    
    "小": {
            "skus": ["3516833"]

    },    
    "蓝-小": {
            "skus": ["3516833"]

    },    
    "C": {
            "skus": ["3516833"]

    },    
    "蓝-C": {
            "skus": ["3516833"]

    },    
    "小-C": {
            "skus": ["3516833"]

    },    
    "蓝-小-C": {
            "skus": ["3516833"]

    }

}

为了更清楚的说明这个算法，再上一张图来解释下吧：

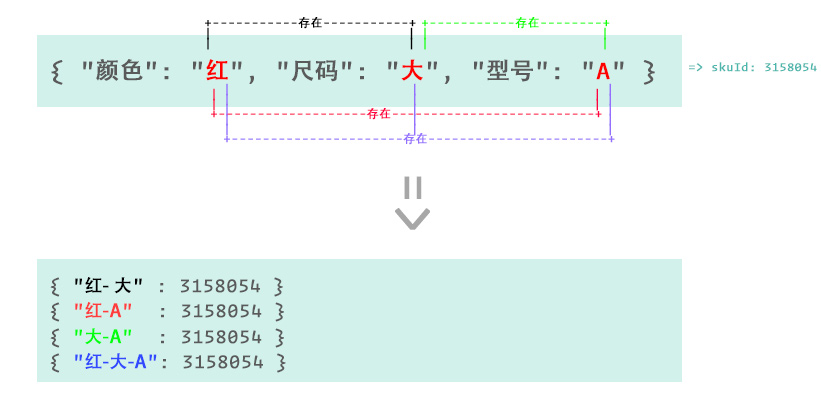
所以根据上面的逻辑得出，计算状态后的界面应该是这样的：

现在这种情况下如果用户点击尺码中应该怎么交互呢？

优化体验

因为当前情况下路径红-中-A 并不存在，如果点击中，那么除了尺码中之外其它的属性中至少有一个属性和中的路径搭配是不存在的。

交互方面需求是：如果不存在就高亮当前属性行，使用户必须选择到可以和中组合存在的属性。而且用户之间选择过的属性要做一次缓存。

所以当点击不存在的属性时交互流程是这样的：

无论当前属性存不存在，先高亮（选中）当前属性
清除其它所有已选属性
更新当前状态（只选当前属性）下的其它属性可选状态
遍历非当前属性行的其它属性查找对应的在缓存中的已选属性
如果缓存中对应的属性存在（可选），则默认选中缓存属性并再次更新其它可选状态。不存在，则高亮当前属性行（深色背景）

这个过程的流程图大概是这样的，点进不存在的属性就会进入「单选流程」

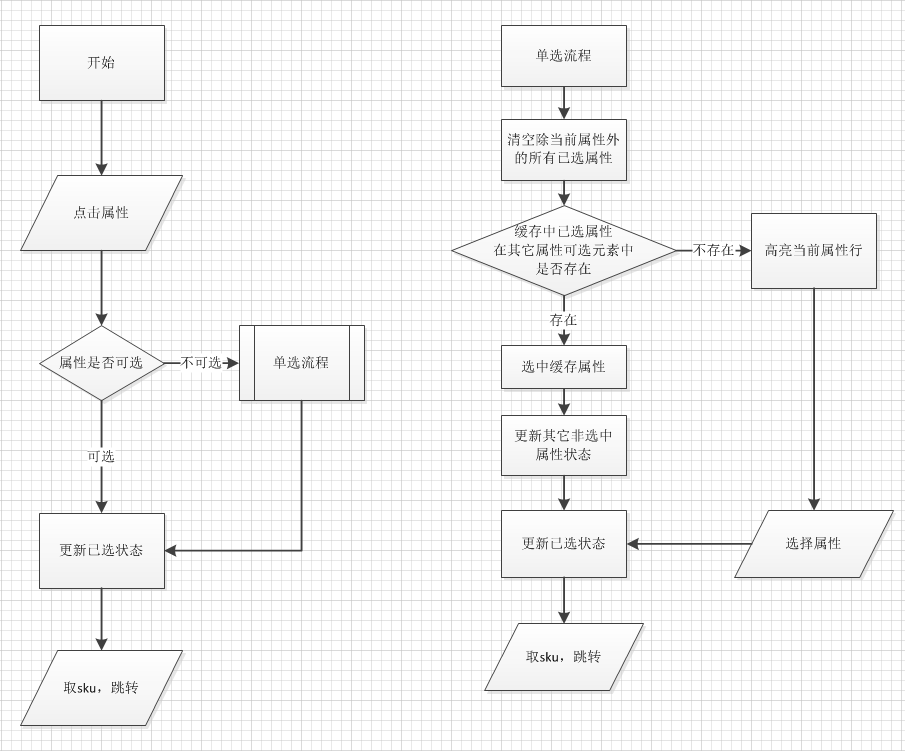
假设后端数据是这样的：

[

   { "颜色": "红", "尺码": "大", "型号": "A", "skuId": "3158054" },

   { "颜色": "白", "尺码": "大", "型号": "A", "skuId": "3158054" }, // 多加了一条

   { "颜色": "白", "尺码": "中", "型号": "B", "skuId": "3133859" },

   { "颜色": "蓝", "尺码": "小", "型号": "C", "skuId": "3516833" }

]

当前选中状态是：白-大-A

如果用户点击中。这个时候白-中是存在的，但是中-A 并不存在，所以保留颜色白，高亮型号属性行：

由此可见和白-中能搭配存在型号只有 B，而缓存的作用就是为了少让用户选一次颜色白。

到这里，基本上主要的功能就实现了。比如库存逻辑处理方式也和不存属性一样，就不再赘述。唯一需要注意的地方是求幂集的复杂度问题。

算法复杂度

幂集算法的时间复杂度是 O(2^n)，也就是说每条数据上面的属性（维度）越多，复杂度越高。SKU数据的多少并不重要，因为是常数级的线性增长，而维度是指数级的增长。

{1}       2^1 = 2=> {},{1}

{1,2}     2^2 = 4=> {},{1},{2},{1,2}

{1,2,3}   2^3 = 8=> {},{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}

...

aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAIAAACQd1PeAAAAGXRFWHRTb2Z0d2FyZQBBZG9iZSBJbWFnZVJlYWR5ccllPAAAAyBpVFh0WE1MOmNvbS5hZG9iZS54bXAAAAAAADw/eHBhY2tldCBiZWdpbj0i77u/IiBpZD0iVzVNME1wQ2VoaUh6cmVTek5UY3prYzlkIj8+IDx4OnhtcG1ldGEgeG1sbnM6eD0iYWRvYmU6bnM6bWV0YS8iIHg6eG1wdGs9IkFkb2JlIFhNUCBDb3JlIDUuMC1jMDYwIDYxLjEzNDc3NywgMjAxMC8wMi8xMi0xNzozMjowMCAgICAgICAgIj4gPHJkZjpSREYgeG1sbnM6cmRmPSJodHRwOi8vd3d3LnczLm9yZy8xOTk5LzAyLzIyLXJkZi1zeW50YXgtbnMjIj4gPHJkZjpEZXNjcmlwdGlvbiByZGY6YWJvdXQ9IiIgeG1sbnM6eG1wPSJodHRwOi8vbnMuYWRvYmUuY29tL3hhcC8xLjAvIiB4bWxuczp4bXBNTT0iaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wL21tLyIgeG1sbnM6c3RSZWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20veGFwLzEuMC9zVHlwZS9SZXNvdXJjZVJlZiMiIHhtcDpDcmVhdG9yVG9vbD0iQWRvYmUgUGhvdG9zaG9wIENTNSBXaW5kb3dzIiB4bXBNTTpJbnN0YW5jZUlEPSJ4bXAuaWlkOkJDQzA1MTVGNkE2MjExRTRBRjEzODVCM0Q0NEVFMjFBIiB4bXBNTTpEb2N1bWVudElEPSJ4bXAuZGlkOkJDQzA1MTYwNkE2MjExRTRBRjEzODVCM0Q0NEVFMjFBIj4gPHhtcE1NOkRlcml2ZWRGcm9tIHN0UmVmOmluc3RhbmNlSUQ9InhtcC5paWQ6QkNDMDUxNUQ2QTYyMTFFNEFGMTM4NUIzRDQ0RUUyMUEiIHN0UmVmOmRvY3VtZW50SUQ9InhtcC5kaWQ6QkNDMDUxNUU2QTYyMTFFNEFGMTM4NUIzRDQ0RUUyMUEiLz4gPC9yZGY6RGVzY3JpcHRpb24+IDwvcmRmOlJERj4gPC94OnhtcG1ldGE+IDw/eHBhY2tldCBlbmQ9InIiPz6p+a6fAAAAD0lEQVR42mJ89/Y1QIABAAWXAsgVS/hWAAAAAElFTkSuQmCC" alt="" />

在 chrome 里面简单跑了几个用例，可见这个算法非常低效，如果要使用这个算法，必须控制维度在合理范围内，而且不仅仅算法时间复杂度很高，生成最后的路径表也会非常大，相应的占用内存也很高。

举个例子：如果有一个 10 维的 sku，那么最终生成的路径表会有 2^10 个（1024） key/value。

最终 demo 可以查看这个： SKU多维属性状态判断（http://codepen.io/keelii/pen/RoOzgb）

相关资料： SKU组合查询算法探索（http://git.shepherdwind.com/sku-search-algorithm.html）