【BZOJ4009_洛谷3242】[HNOI2015] 接水果（整体二分）

题目：

洛谷 3242

分析：

明确题意：在一棵树上给定若干权值为 \(w\) 的路径 \((u,v)\) （盘子），每次给定 \((a,b)\) （水果），询问所有满足 \((u,v)\) 被 \((a,b)\) 完全覆盖的路径中第 \(k\) 小的路径的权值。

先考虑如何快速判断 \((u,v)\) 是不是 \((a,b)\) 的子路径。第一反应是充要条件是 \(a\) 和 \(b\) 分别在 \(u\) 和 \(v\) 的子树中（设 \(\mathrm{dfn}_p\) 是 \(p\) 在 dfs 序中的位置，以下默认 \(\mathrm{dfn}_u<\mathrm{dfn}_v\) 且 \(\mathrm{dfn}_a<\mathrm{dfn}_b\) ）。这对于大部分情况是成立的，但是当 \(u\) 是 \(v\) 的祖先时并不成立，因为 \(v\) 的子树被包含在 \(u\) 的子树中，所以而在 \(v\) 的子树中任选两点都满足条件，但之间的路径并不能覆盖 \((u,v)\) 。画图可知，此时 \(b\) 仍要求在 \(v\) 的子树中，而 \(a\) 应当在 \(p\) 的子树外（注意不是 \(u\) 的子树），其中 \(p\) 是从 \(u\) 到 \(v\) 的路径上除 \(u\) 之外的第一个点。详见下图（博客特色画风）：

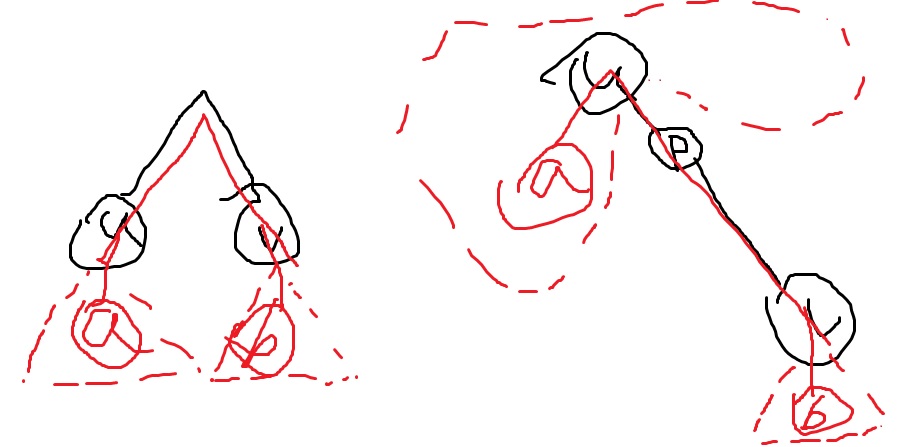
总结一下，如果 \((u,v)\) 被 \((a,b)\) 完全覆盖，那么需要满足：

如果 \((u,v)\) 不是一条深度递增的链，那么需要满足（ \(\mathrm{out}_p\) 表示 \(p\) 的子树中最大的 \(\mathrm{dfn}\) ）：

\[\mathrm{dfn}_a\in [\mathrm{dfn}_u,\mathrm{out}_u]\ 且\ \mathrm{dfn}_b\in [\mathrm{dfn}_v,\mathrm{out}_v]
\]

否则需要满足（ \(p\) 的含义见上）：

\[\mathrm{dfn}_a\in [1,\mathrm{dfn}_p)\cup (\mathrm{out}_p,n]\ 且\ \mathrm{dfn}_b\in [\mathrm{dfn}_v,\mathrm{out}_v]
\]

对于求第 \(k\) 小的题，一个很常见的策略是二分。二分一个答案 \(x\) ，把所有权值小于等于 \(x\) 的点都插入数据结构，然后查询符合要求的点的数量，若大于等于 \(k\) 则向下二分，否则向上二分。

对于这道题，由于限制是二维的，所以需要树套树。插入一个路径 \((u,v)\) 相当于给它能贡献到的地方的答案全部加 1 。对于 \(u\) 不是 \(v\) 的祖先的情况，这个「地方」是一维范围为 \([\mathrm{dfn}_u,\mathrm{out}_u]\) ，另一维范围为 \([\mathrm{dfn}_v,\mathrm{out}_v]\) 的矩形；否则，贡献到的是两个矩形（自行根据上面的式子构造）。查询一个路径 \((a,b)\) 相当于查询点 \((\mathrm{dfn}_a,\mathrm{dfn}_b)\) 的权值。由于是多组询问，所以套上整体二分，时间复杂度 \(O(n\log^3 n)\) 。

然而实测树套树会不幸被 卡常 卡复杂度。可以用类似离线扫描线的思想，把修改和询问按第一维的 dfn 排序，然后按 dfn 从小到大处理，并把修改拆成两次： 在 \(\mathrm{dfn}_u\) 处给 \([\mathrm{dfn}_v,\mathrm{out}_v]\) 加 1 ，在 \(\mathrm{out}_u+1\) 处给上述区间减 1 。用树状数组维护区间修改和单点查询，时间复杂度 \(O(n\log^2 n)\) 。

代码：

#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
namespace zyt
{
	template<typename T>
	inline bool read(T &x)
	{
		char c;
		bool f = false;
		x = 0;
		do
			c = getchar();
		while (c != EOF && c != '-' && !isdigit(c));
		if (c == EOF)
			return true;
		if (c == '-')
			f = true, c = getchar();
		do
			x = x * 10 + c - '0', c = getchar();
		while (isdigit(c));
		if (f)
			x = -x;
		return true;
	}
	template<typename T>
	inline void write(T x)
	{
		static char buf[20];
		char *pos = buf;
		if (x < 0)
			putchar('-'), x = -x;
		do
			*pos++ = x % 10 + '0';
		while (x /= 10);
		while (pos > buf)
			putchar(*--pos);
	}
	const int N = 4e4 + 10, B = 16;
	int n, head[N], ecnt, fa[N][B], dep[N], dfn[N], dfncnt, out[N], id[N], ans[N];
	struct edge
	{
		int to, next;
	}e[N << 1];
	struct _plt
	{
		int u, v, c, nxt;
		bool operator < (const _plt &b) const
		{
			return c < b.c;
		}
	}plt[N]; // plate
	int idplt[N];
	struct _frt
	{
		int u, v, k, id;
	}frt[N]; // fruit
	bool cmpdfnu(const int a, const int b)
	{
		return dfn[frt[a].u] < dfn[frt[b].u];
	}
	namespace Tree_Array
	{
		int data[N];
		inline int lowbit(const int x)
		{
			return x & (-x);
		}
		void add(int a, const int x)
		{
			while (a <= n)
				data[a] += x, a += lowbit(a);
		}
		int query(int a)
		{
			int ans = 0;
			while (a)
				ans += data[a], a -= lowbit(a);
			return ans;
		}
		void add(const int l, const int r, const int x)
		{
			add(l, x), add(r + 1, -x);
		}
	}
	void add(const int a, const int b)
	{
		e[ecnt] = (edge){b, head[a]}, head[a] = ecnt++;
	}
	void dfs(const int u, const int f)
	{
		fa[u][0] = f;
		for (int i = 1; i < B; i++)
			fa[u][i] = fa[fa[u][i - 1]][i - 1];
		dep[u] = dep[f] + 1;
		dfn[u] = ++dfncnt;
		for (int i = head[u]; ~i; i = e[i].next)
		{
			int v = e[i].to;
			if (v == f)
				continue;
			dfs(v, u);
		}
		out[u] = dfncnt;
	}
	inline int lca(int a, int b)
	{
		if (dep[a] < dep[b])
			swap(a, b);
		for (int i = B - 1; i >= 0; i--)
			if (dep[fa[a][i]] >= dep[b])
				a = fa[a][i];
		if (a == b)
			return a;
		for (int i = B - 1; i >= 0; i--)
			if (fa[a][i] != fa[b][i])
				a = fa[a][i], b = fa[b][i];
		return fa[a][0];
	}
	namespace Divide_Together
	{
		struct _mdf
		{
			int pos, l, r, x;
			_mdf() {}
			_mdf(const int _pos, const int _l, const int _r, const int _x)
				: pos(_pos), l(_l), r(_r), x(_x) {}
			bool operator < (const _mdf &b) const
			{
				return pos < b.pos;
			}
		}mdf[N << 1];
		int cnt;
		void insert(const int l, const int r, const int ll, const int rr, const int x)
		{
			mdf[cnt++] = _mdf(l, ll, rr, x);
			mdf[cnt++] = _mdf(r + 1, ll, rr, -x);
		}
		void insert(const int i, const int x)
		{
			if (plt[i].nxt)
			{
				insert(1, dfn[plt[i].nxt] - 1, dfn[plt[i].v], out[plt[i].v], x);
				if (out[plt[i].nxt] < n)
					insert(dfn[plt[i].v], out[plt[i].v], out[plt[i].nxt] + 1, n, x);
			}
			else
				insert(dfn[plt[i].u], out[plt[i].u], dfn[plt[i].v], out[plt[i].v], x);
		}
		void solve(const int l, const int r, const int ql, const int qr)
		{
			using Tree_Array::query;
			using Tree_Array::add;
			if (l == r)
			{
				for (int i = ql; i <= qr; i++)
					ans[frt[id[i]].id] = plt[l].c;
				return;
			}
			static int buf1[N], buf2[N];
			int cnt1 = 0, cnt2 = 0;
			int mid = (l + r) >> 1;
			cnt = 0;
			for (int i = l; i <= mid; i++)
				insert(i, 1);
			sort(mdf, mdf + cnt);
			int now = 0;
			for (int i = ql; i <= qr; i++)
			{
				while (now < cnt && mdf[now].pos <= dfn[frt[id[i]].u])
					add(mdf[now].l, mdf[now].r, mdf[now].x), ++now;
				int tmp = query(dfn[frt[id[i]].v]);
				if (tmp >= frt[id[i]].k)
					buf1[cnt1++] = id[i];
				else
					buf2[cnt2++] = id[i], frt[id[i]].k -= tmp;
			}
			for (int i = 0; i < cnt1; i++)
				id[i + ql] = buf1[i];
			for (int i = 0; i < cnt2; i++)
				id[i + cnt1 + ql] = buf2[i];
			for (int i = 0; i < now; i++)
				add(mdf[i].l, mdf[i].r, -mdf[i].x);
			solve(l, mid, ql, ql + cnt1 - 1);
			solve(mid + 1, r, ql + cnt1, qr);
		}
	}
	int work()
	{
		int p, q;
		read(n), read(p), read(q);
		memset(head, -1, sizeof(int[n + 1]));
		for (int i = 1; i < n; i++)
		{
			int a, b;
			read(a), read(b);
			add(a, b), add(b, a);
		}
		dfs(1, 0);
		for (int i = 0; i < p; i++)
		{
			read(plt[i].u), read(plt[i].v), read(plt[i].c);
			if (dfn[plt[i].u] > dfn[plt[i].v])
				swap(plt[i].u, plt[i].v);
			plt[i].nxt = 0;
			if (lca(plt[i].u, plt[i].v) == plt[i].u)
			{
				int &tmp = plt[i].nxt;
				tmp = plt[i].v;
				for (int j = B - 1; j >= 0; j--)
					if (dep[fa[tmp][j]] > dep[plt[i].u])
						tmp = fa[tmp][j];
			}
		}
		sort(plt, plt + p);
		for (int i = 0; i < q; i++)
		{
			id[i] = i;
			read(frt[i].u), read(frt[i].v), read(frt[i].k);
			if (dfn[frt[i].u] > dfn[frt[i].v])
				swap(frt[i].u, frt[i].v);
			frt[i].id = i;
		}
		sort(id, id + q, cmpdfnu);
		Divide_Together::solve(0, p - 1, 0, q - 1);
		for (int i = 0; i < q; i++)
			write(ans[i]), putchar('\n');
		return 0;
	}
}
int main()
{
	return zyt::work();
}