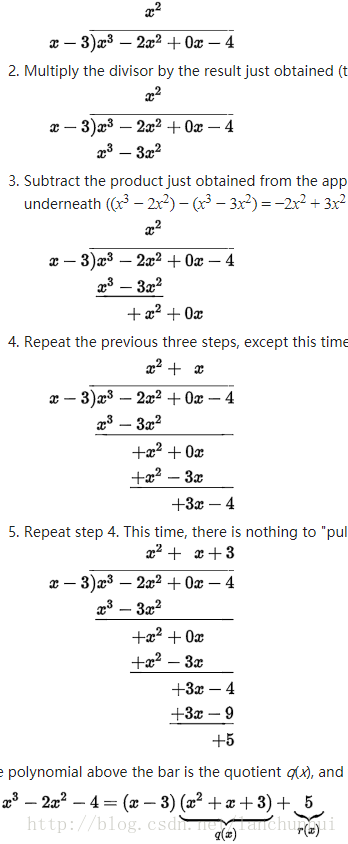(多项式)因式分解定理(Factor theorem)与多项式剩余定理(Polynomial remainder theorem)(多项式长除法)
(多项式的)因式分解定理(factor theorem)是多项式剩余定理的特殊情况,也就是余项为 0 的情形。
0. 多项式长除法(Polynomial long division)
Polynomial long division - Wikipedia
1. 因式分解定理
该定理表达的是,多项式 f(x) 存在因子 x−k 当且仅当 f(k)=0(余数为 0,也即 k 是其根)。
对于多项式 f(x)=x3+7x2+8x+2,
- x−1 是否为其因子?f(1)≠0
- x+1 是否为其因子?f(−1)=0,故为其因子;
(多项式除法)又有 x3+7x2+8x+2x+1=x2+6x+2,因此 x+1 与 x2+6x+2 均为其因子。
2. 多项式余项定理
举例对于多项式 f(x)=x3−12x2−42,当除数为 x−3 时,商为 x2−9x−27,余项为 −123。也即,f(x)=(x−3)(x2−9x−27)−123。因此 f(3)=−123。
更为一般地,对于二次多项式 f(x)=ax2+bx+c,有如下的等式变换:
所以:
(多项式)因式分解定理(Factor theorem)与多项式剩余定理(Polynomial remainder theorem)(多项式长除法)的更多相关文章
- DHU 1788 Chinese remainder theorem again 中国剩余定理
Chinese remainder theorem again Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 ...
- HDU 1788 Chinese remainder theorem again 中国剩余定理
题意: 给定n,AA 以下n个数m1,m2···mn 则有n条方程 res % m1 = m1-AA res % m2 = m2-AA 问res的最小值 直接上剩余定理,嘿嘿 #include< ...
- 2019牛客暑期多校训练营(第七场)D Number——实系数多项式因式分解定理
前置知识 代数基本定理 定理:每个次数 ≥ 1 复系数多项式在复数域中至少有一个跟. 由此推出,n次复系数多项式方程在复数域内有且只有n个根(重根按重数计算).(只要不断把多项式除以(x-xa),即可 ...
- hdu 1788 Chinese remainder theorem again(最小公倍数)
Problem Description 我知道部分同学最近在看中国剩余定理,就这个定理本身,还是比较简单的: 假设m1,m2,-,mk两两互素,则下面同余方程组: x≡a1(mod m1) x≡a2( ...
- Chinese remainder theorem again(中国剩余定理)
C - Chinese remainder theorem again Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:% ...
- 《孙子算经》之"物不知数"题:中国剩余定理
1.<孙子算经>之"物不知数"题 今有物不知其数,三三数之剩二,五五数之剩七,七七数之剩二,问物几何? 2.中国剩余定理 定义: 设 a,b,m 都是整数. 如果 m ...
- POJ 1006 中国剩余定理
#include <cstdio> int main() { // freopen("in.txt","r",stdin); ; while(sca ...
- [TCO 2012 Round 3A Level3] CowsMooing (数论,中国剩余定理,同余方程)
题目:http://community.topcoder.com/stat?c=problem_statement&pm=12083 这道题还是挺耐想的(至少对我来说是这样).开始时我只会60 ...
- poj1006中国剩余定理
Biorhythms Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 103506 Accepted: 31995 Des ...
随机推荐
- nfs服务权限配置
nfs服务权限配置 1. 查看系统是否已经安装了服务Rpm -qa | grep nfs 2. 启动服务,并且开机自动运行Systemctl start nfsSystemctl enabled nf ...
- Git 分支使用
一个主分支肯定是不够用的,不同的开发最好放在不同的分支上,在最后进行合并,不然在开发中会相互干扰. PS:环境Window xp,Git-1.8.4-preview20130916(http://gi ...
- 最长上升子序列(动态规划递推,LIS)
1759:最长上升子序列 题目: 总时间限制: 2000ms 内存限制: 65536kB 描述 一个数的序列bi,当b1 < b2 < ... < bS的时候,我们称这个序列是上升的 ...
- 在mac上面运行cherrytree
下载源码包 wget http://www.giuspen.com/software/cherrytree-0.38.4.tar.xz 解压 tar -xvf cherrytree-0.38.4.ta ...
- Python进阶-打包程序为exe
操作系统:win7 x64 运行环境:Python3.5 安装PyInstaller 第一步:下载PyInstaller https://github.com/pyinstaller/pyinstal ...
- airfoil polar data during post stall stages (high AOA)
airfoil polar data during post stall stages (high AOA) Table of Contents 1. airfoil polar during pos ...
- 【Codeforces 382C】Arithmetic Progression
[链接] 我是链接,点我呀:) [题意] 让你在n个数字中再加入一个数字 使得这n+1个数字排序之后 相邻两个数字的差都相同 [题解] 注意相邻为0的情况 这种情况 只有全都相同才行 只有一种情况 然 ...
- nyoj 93 汉诺塔(三)(stack)
汉诺塔(三) 时间限制:3000 ms | 内存限制:65535 KB 难度:3 描述 在印度,有这么一个古老的传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针.印度 ...
- [luoguP1417] 烹调方案(背包DP)
传送门 By tinylic 如果没有b[i]这个属性的话就是明显的01背包问题. 现在考虑相邻的两个物品x,y.假设现在已经耗费p的时间,那么分别列出先做x,y的代价: a[x]-(p+c[x])* ...
- Java 学习(6):java Number & Math & String & 数组...常用类型
目录 --- Number & Math类 --- Character 类 --- String 类 --- StringBuffer 类 --- 数组 Number & Math类: ...