最长回文子串问题 O(n)算法 manacher URAL1297 HDU3068

先来看一道简单的题，ural1297 给定一个1000长度的字符串，求最长回文子串。

看起来很Naive，乱搞一下，O（n^2）都可以解决。

再来看这个题 HDU3068 120个110000长度的字符串，是不是感觉有点困难了？据说后缀数组也要TLE

给出一个O（n）的解决方案 manacher算法 很有趣的利用了回文子串的性质，进行递推更新。

转载自http://blog.csdn.net/ggggiqnypgjg/article/details/6645824

这里，我介绍一下O（n）回文串处理的一种方法。Manacher算法.
原文地址：
http://zhuhongcheng.wordpress.com/2009/08/02/a-simple-linear-time-algorithm-for-finding-longest-palindrome-sub-string/
    其实原文说得是比较清楚的，只是英文的，我这里写一份中文的吧。
    首先：大家都知道什么叫回文串吧，这个算法要解决的就是一个字符串中最长的回文子串有多长。这个算法可以在O（n）的时间复杂度内既线性时间复杂度的情况下，求出以每个字符为中心的最长回文有多长，
    这个算法有一个很巧妙的地方，它把奇数的回文串和偶数的回文串统一起来考虑了。这一点一直是在做回文串问题中时比较烦的地方。这个算法还有一个很好的地方就是充分利用了字符匹配的特殊性，避免了大量不必要的重复匹配。
    算法大致过程是这样。先在每两个相邻字符中间插入一个分隔符，当然这个分隔符要在原串中没有出现过。一般可以用‘#’分隔。这样就非常巧妙的将奇数长度回文串与偶数长度回文串统一起来考虑了（见下面的一个例子，回文串长度全为奇数了），然后用一个辅助数组P记录以每个字符为中心的最长回文串的信息。P［id］记录的是以字符str［id］为中心的最长回文串，当以str［id］为第一个字符，这个最长回文串向右延伸了P［id］个字符。
    原串：    w aa bwsw f d
    新串：   # w# a # a # b# w # s # w # f # d #
辅助数组P：  1 2 1 2 3 2 1 2 1 2 1 4 1 2 1 2 1 2 1
    这里有一个很好的性质，P［id］-1就是该回文子串在原串中的长度（包括‘#’）。如果这里不是特别清楚，可以自己拿出纸来画一画，自己体会体会。当然这里可能每个人写法不尽相同，不过我想大致思路应该是一样的吧。
    好，我们继续。现在的关键问题就在于怎么在O（n）时间复杂度内求出P数组了。只要把这个P数组求出来，最长回文子串就可以直接扫一遍得出来了。
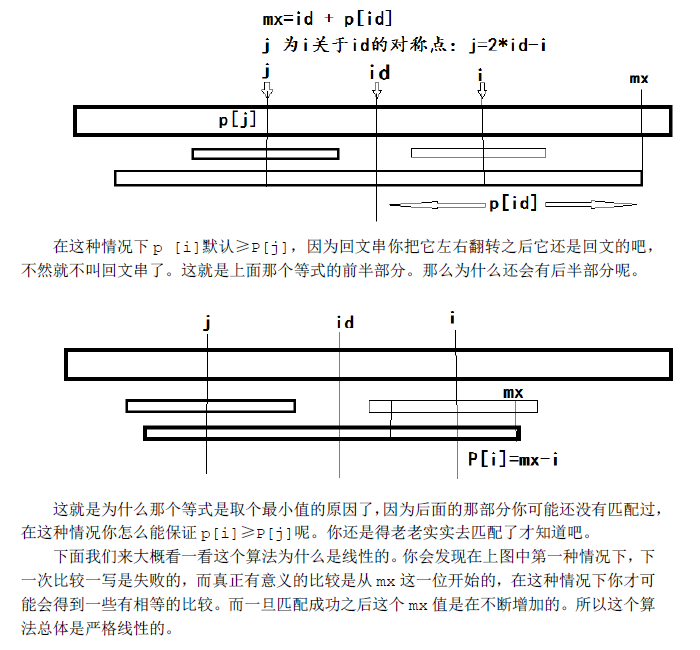
    由于这个算法是线性从前往后扫的。那么当我们准备求P［i］的时候，i以前的P［j］我们是已经得到了的。我们用mx记在i之前的回文串中，延伸至最右端的位置。同时用id这个变量记下取得这个最优mx时的id值。（注：为了防止字符比较的时候越界，我在这个加了‘#’的字符串之前还加了另一个特殊字符‘$’，故我的新串下标是从1开始的）
好，到这里，我们可以先贴一份代码了。

 

复制代码

1. void pk()
   {
       int i;
       int mx = 0;
       int id;
       for(i=1; i<n; i++)
       {
           if( mx > i )
               p[i] = MIN( p[2*id-i], mx-i );        
           else
               p[i] = 1;
           for(; str[i+p[i]] == str[i-p[i]]; p[i]++)
               ;
           if( p[i] + i > mx )
           {
               mx = p[i] + i;
               id = i;
           }
       }
   }

   代码是不是很短啊，而且相当好写。很方便吧，还记得我上面说的这个算法避免了很多不必要的重复匹配吧。这是什么意思呢，其实这就是一句代码。

 

if( mx > i)

    p[i]=MIN( p[2*id-i], mx-i);

 

就是当前面比较的最远长度mx>i的时候，P［i］有一个最小值。这个算法的核心思想就在这里，为什么P数组满足这样一个性质呢?

   （下面的部分为图片形式）

 

    看完这个算法，你有可能会觉得这种算法在哪会用到呢？其实回文串后缀数组也可以做。只是复杂度是O（n log n）的，而且一般情况下也不会刻意去卡一个log n的算法。可正好hdu就有这么一题，你用后缀数组写怎么都得T（当然应该是我写得太烂了）。不信的话大家也可以去试试这题。

 

给出HDU3068的代码 很简单

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>

using namespace std;

const int maxn=310000+1;

int   find_palindrome(char str[],int sym[],int len[],int n)//需要对数组sym在外部进行初始化
{
 int maxl=1;
 sym[0]=1;
 for(int i=1,j=0;i<(n<<1)-1;++i)
 	{
 	 int p=i>>1,q=i-p,r=((j+1)>>1)+sym[j]-1;
 	 sym[i]=r<q ? 0:min(r-q+1,sym[(j<<1)-i]);
 	 while(p>sym[i]-1&&q+sym[i]<n&&str[p-sym[i]]==str[q+sym[i]])
 	    ++sym[i];
	 if(q+sym[i]-1>r)
	 	j=i;
	}
 for(int i=0;i<n;i++)
 	len[i]=1;
 for(int i=0;i<n;i++)
 	{
 	 int ls=i-sym[i*2]+1;
 	 if(ls<0)continue;
 	 len[ls]=max(len[ls],sym[i*2]*2-1);
 	 maxl=max(maxl,len[ls]);
 	 if(sym[i*2+1]==0)continue;
 	 ls=i-sym[i*2+1]+1;
 	 if(ls<0)continue;
 	 len[ls]=max(len[ls],sym[i*2+1]*2);
 	 maxl=max(maxl,len[ls]);
	}
 return maxl;
}

char str[maxn];
 int len[maxn*2],ans[maxn];
int main()
{ios::sync_with_stdio(false);
freopen("t.txt","r",stdin);

 while(cin>>str)
 {

    memset(len,0,sizeof(len));
 	 cout<<find_palindrome(str,len,ans,strlen(str))<<endl;
 	 memset(str,0,sizeof(str));

 }
 return 0;
}