luoguP4022 [CTSC2012]熟悉的文章

题意

显然这个\(L\)是可以二分的，我们只需要判断\(L\)是否合法即可。

显然有一个\(O(n^2)\)的DP：

设\(f_i\)表示当前匹配到\(i\)的最大匹配长度。

\(f_i=max(f_j+i-(j+1)+1)\ j\in[i-match_i,i-L]\)

其中的\(match_i\)表示前缀\(i\)能和文本库匹配的最长后缀长度，这显然是可以在后缀自动机上匹配求出的。

于是就可以\(O(n^2logn)\)做了。

发现\(i-match_i\)单调递增，于是可以单调队列解决。

证明：

反证即可，如果不单调必定是如下情况：



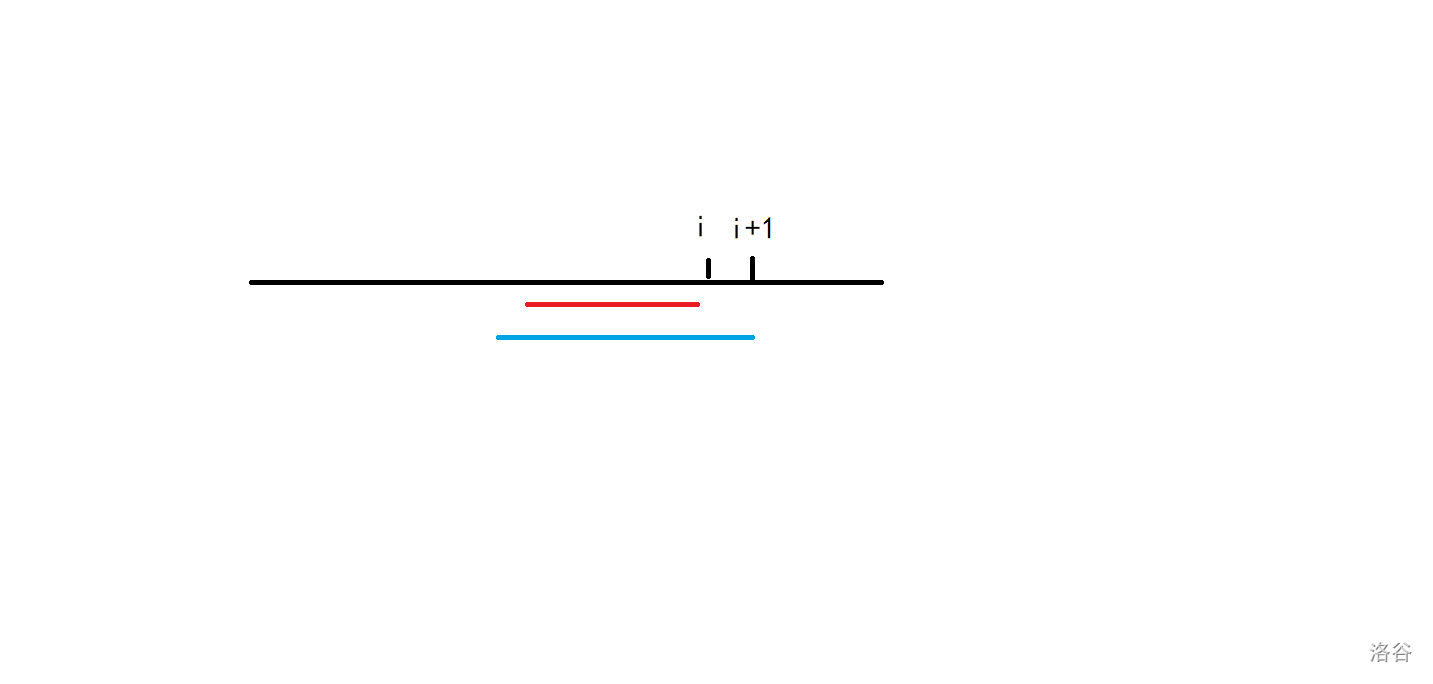
红线是i匹配的长度，蓝线是i+1匹配的长度，显然i能匹配更长。

code:

#include<bits/stdc++.h>
using namespace std;
const int maxn=2*1e6+10;
int n,m;
int match[maxn],f[maxn],q[maxn];
char s[maxn];
struct SAM
{
	int last,tot;
	int fa[maxn],len[maxn];
	int ch[maxn][2];
	SAM(){last=tot=1;}
	inline void add(int c)
	{
		if(ch[last][c]&&len[last]+1==len[ch[last][c]]){last=ch[last][c];return;}
		int now=++tot;len[now]=len[last]+1;
		int p=last;
		while(p&&!ch[p][c])ch[p][c]=now,p=fa[p];
		if(!p){fa[now]=1;last=now;return;}
		int q=ch[p][c];bool flag=0;
		if(len[q]==len[p]+1)fa[now]=q;
		else
		{
			if(p==last)flag=1;
			int nowq=++tot;len[nowq]=len[p]+1;
			memcpy(ch[nowq],ch[q],sizeof(ch[q]));
			fa[nowq]=fa[q],fa[q]=fa[now]=nowq;
			while(p&&ch[p][c]==q)ch[p][c]=nowq,p=fa[p];
			if(flag)last=nowq;
		}
		if(!flag)last=now;
	}
}sam;
inline void getmatch(char* s)
{
	int len=strlen(s+1),now=1,nowl=0;
	for(int i=1;i<=len;i++)
	{
		while(now&&!sam.ch[now][s[i]-'0'])now=sam.fa[now],nowl=sam.len[now];
		if(now)now=sam.ch[now][s[i]-'0'],nowl++;
		else now=1,nowl=0;
		match[i]=nowl;
	}
}
inline bool check(int mid,char* s)
{
	int l=1,r=0,len=strlen(s+1);
	for(int i=0;i<mid;i++)f[i]=0;
	for(int i=mid;i<=len;i++)
	{
		f[i]=f[i-1];
		while(l<=r&&f[q[r]]-q[r]<=f[i-mid]-(i-mid))r--;
		q[++r]=i-mid;
		while(l<=r&&q[l]<i-match[i])l++;
		if(l<=r)f[i]=max(f[i],i+f[q[l]]-q[l]);
	}
	return f[len]*10>=len*9;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		sam.last=1;
		scanf("%s",s+1);
		int len=strlen(s+1);
		for(int j=1;j<=len;j++)sam.add(s[j]-'0');
	}
	for(int i=1;i<=n;i++)
	{
		scanf("%s",s+1);
		getmatch(s);
		int l=0,r=strlen(s+1),ans=0;
		while(l<=r)
		{
			int mid=(l+r)>>1;
			if(check(mid,s))ans=mid,l=mid+1;
			else r=mid-1;
		}
		printf("%d\n",ans);
	}
	return 0;
}