机器学习中的误差 Where does error come from？

误差来自于偏差和方差（bias and variance）

 

对于随机变量 X，假设其期望和方差分别为 μ 和 σ²。随机采样 N 个随机变量构成样本，计算算术平均值 m，并不会直接得到 μ （除非采样无穷多个样本点）。

 

假设 m 和 s² 是样本均值和样本方差，由于样本都是随机抽取的，m 和 s² 也是随机的，那么如何构造的 μ  的 estimator？

如果采样很多次，每次都计算得到一个不同的 m，对这些变量 m 求期望，得到的就是对随机变量 X 的均值 μ 的估计：

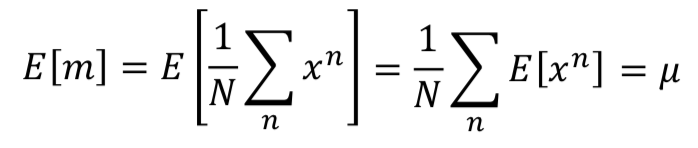，所以对随机变量 X 的均值的估计是无偏的。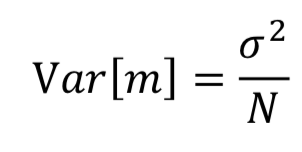

 

再对 m 求方差，根据定义，1/N 拿出来会套一个平方，而每次采样都是独立的，所以：

接下来，如何构造 σ² 的 estimator？=> 按照定义应该是对 s² 求期望：

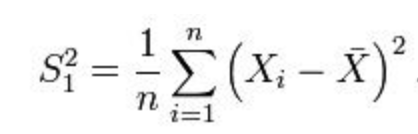
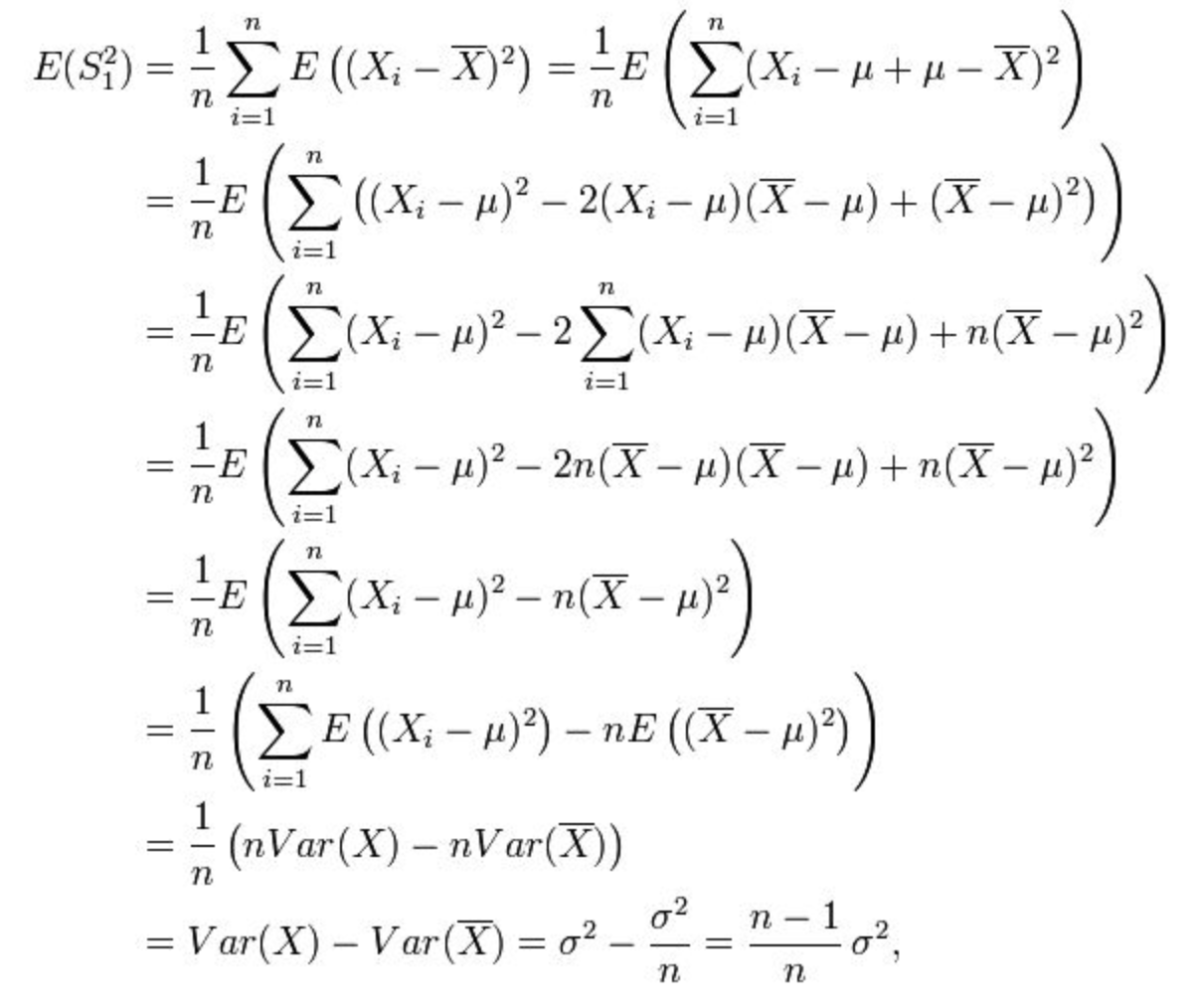
可以发现这个估计是有偏的，修正：

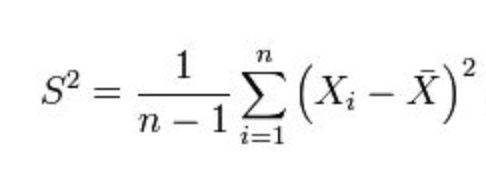
回到机器学习的误差问题上，以 linear regression 为例：

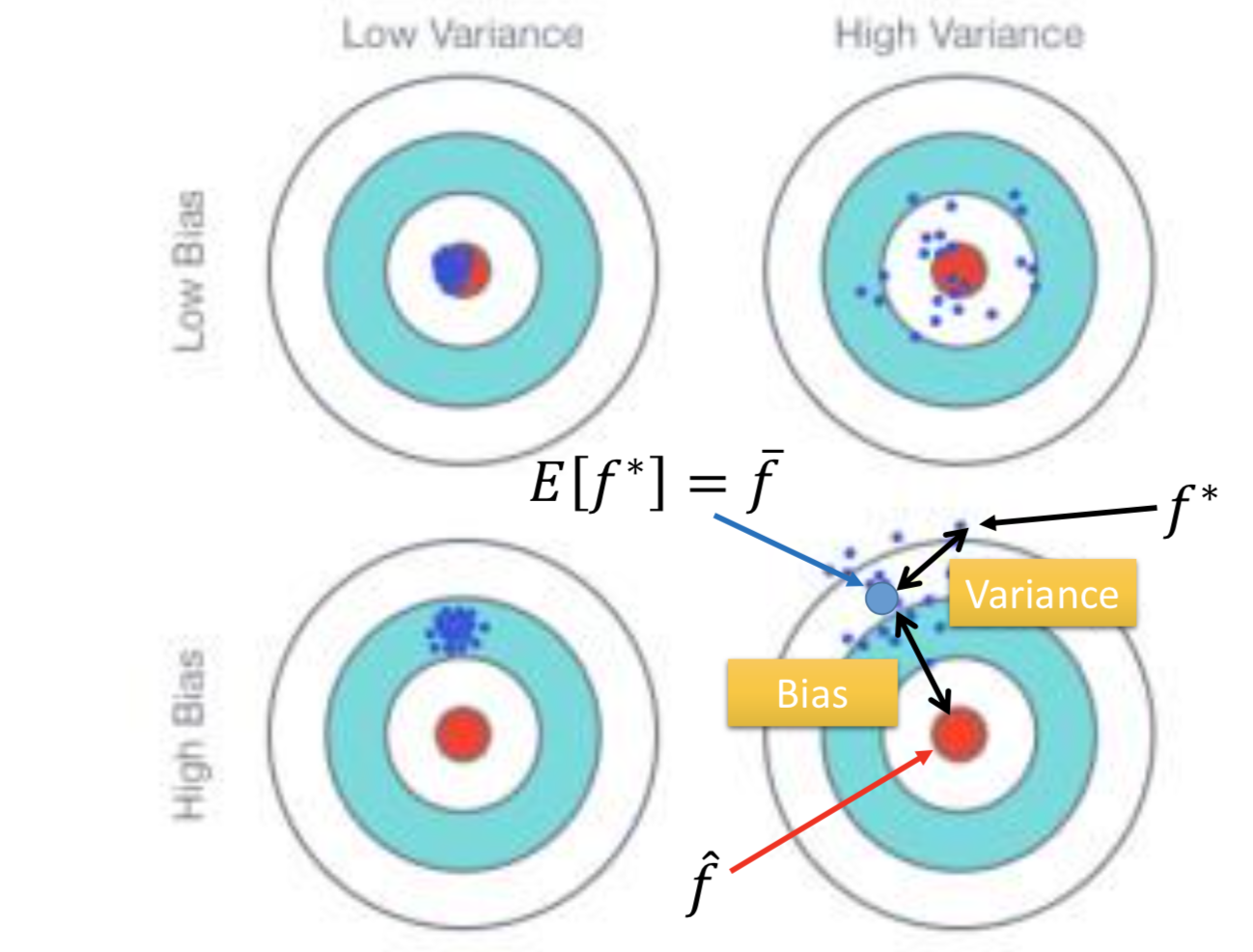
同一个模型，怎么找很多个 f^* 呢？——做很多次实验就好了。

为什么简单的模型比较不容易产生高方差的误差？

因为简单的模型受不同训练数据选取的影响不太大，而复杂模型的结果就会因此散布的很开(large variance)。

 

 

为什么简单模型的偏差误差可能比较大？

直观解释，简单模型的 function 的空间比较小，当定义模型之后就意味着最好的一个模型只能从这组 function set 中选出来，可能这个比较小的函数空间并没有包含到要找的 target，所以偏差会比较大。

 

复杂模型比较不容易出现高偏差的误差（蓝色线是红色线的平均，黑色线是 target）：

underfitting:  Large bias, Small variance

overfitting:  Large variance, Small bias

怎么处理两类误差？

如果模型不能很好的拟合训练数据，就是 large bias  => 更复杂的模型；增加更多特征

 如果可以很好的拟合训练数据，但不能很好但拟合测试数据，就是 large variance  => 收集更多数据，数据增强；如果收集不到数据了，增加正则化惩罚项

 

 

怎么选择模型？

可靠的做法：cross validation

把训练集分成 training set 和 validation set 两部分，这样模型在 testing set 的 pubilc 上的表现就可以比较好的代表其在private集上的表现。（没有靠任何测试集信息决定模型）

 

更进一步的方法：先把训练集分成 N 个等份，分别作为 val 训练，取最优平均误差的模型，固定后再用全部的训练集训练一次