主席树学习笔记（静态区间第k大）

题目背景

这是个非常经典的主席树入门题——静态区间第K小

数据已经过加强，请使用主席树。同时请注意常数优化

题目描述

如题，给定N个整数构成的序列，将对于指定的闭区间查询其区间内的第K小值。

输入输出格式

输入格式：

第一行包含两个正整数N、M，分别表示序列的长度和查询的个数。

第二行包含N个整数，表示这个序列各项的数字。

接下来M行每行包含三个整数l, r, kl,r,k , 表示查询区间[l, r][l,r]内的第k小值。

输出格式：

输出包含k行，每行1个整数，依次表示每一次查询的结果

输入输出样例

输入样例#1： 复制

5 5
25957 6405 15770 26287 26465
2 2 1
3 4 1
4 5 1
1 2 2
4 4 1

输出样例#1： 复制

6405
15770
26287
25957
26287

题面非常清晰，区间第k大。首先，每次排序再还原肯定是要跪的。

这时主席树就出现了。

主席树，倒不如说是榕树（有多个根节点，但是却不是森林）。可以说是在用空间换时间。

其实这题，主席树的主体应该是一棵权值线段树。

别人都说主席树是在每个位置维护了一颗线段树，我一直以为是每一个叶节点，其实是在每一个...好吧就是叶节点。

这里可能要把历史值那一题拿出来讲讲，主席树的每一次修改只修改一条链，而不是整个换血，所以为我们的查询提供了方便。

模拟一发：

7 1

1 5 2 6 3 7 4

建树：(感谢@bestFy的数据和图！)

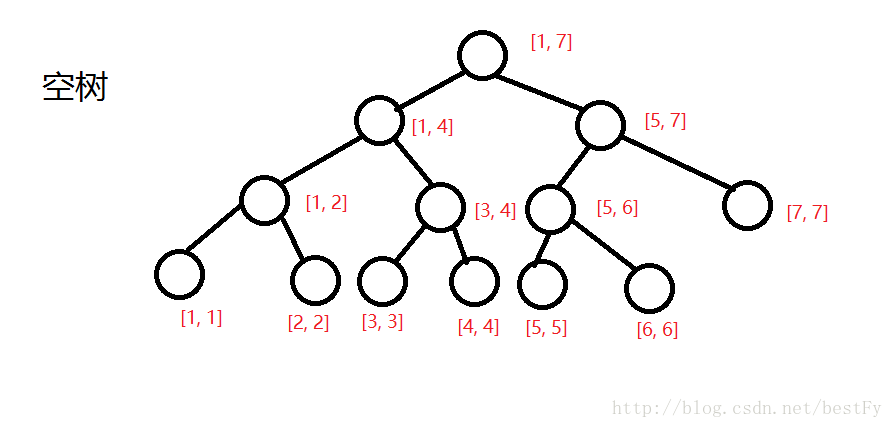
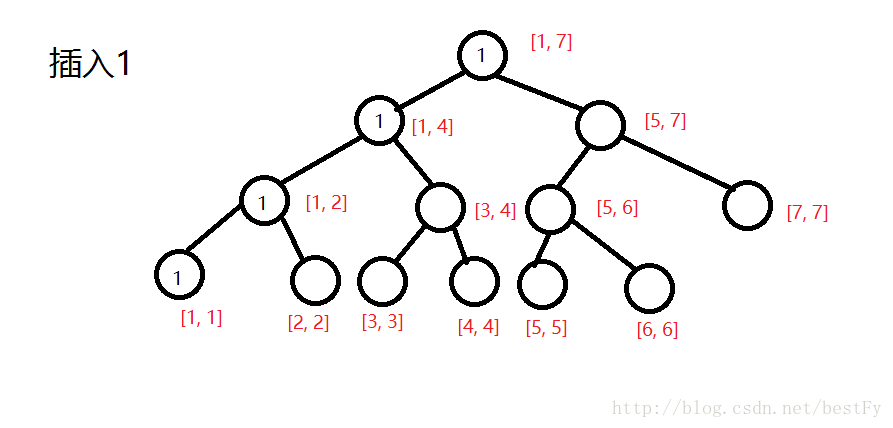
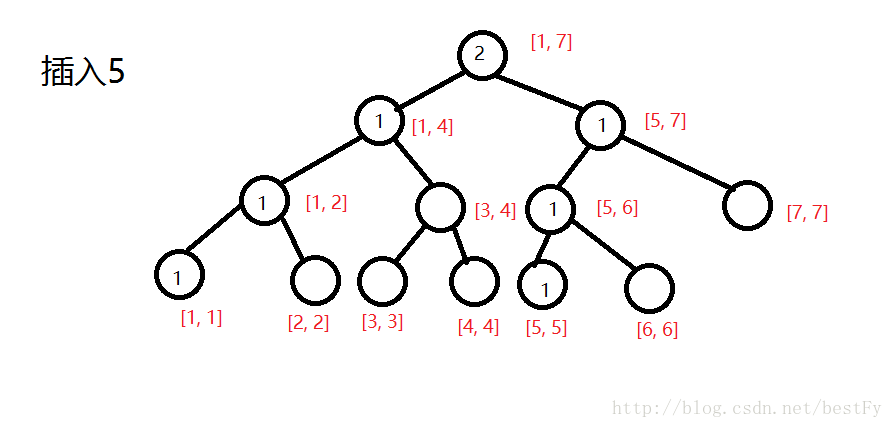
插完所有的之后：

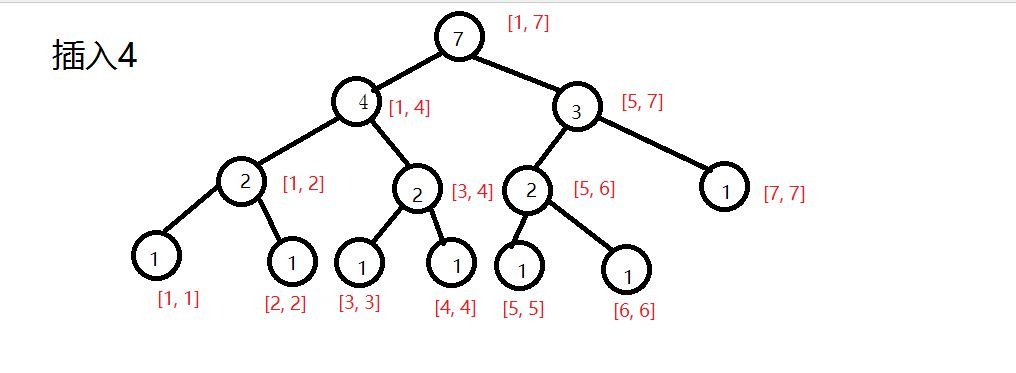
（妥妥的权值线段树）

最终图只是最后一棵线段树的样子，之前的各个线段树依旧在保存着。

于是就出现了旧节点和新建的节点公用一个根节点的情况。于是就可以愉快地进行差分了（因为两个新旧节点是等价的啊）

∴两棵线段树的对应节点相减就是对应区间有的数字啦

所以对于一个区间[l, r]，我们可以每次算出在[l, mid]范围内的数，如果数量>=k（k就是第k大），就往左子树走，否则就往右子树走。

于是区间第k大就完成了。

贴代码：

#include<bits/stdc++.h>
变量解释：sum：节点的总数
rt：新旧树的根节点
ls：左儿子
rs：右儿子
tot：当前节点编号
using namespace std;
const int maxn=;
int n,m,tot,sum[maxn<<],rt[maxn<<],ls[maxn<<],rs[maxn<<],a[maxn],b[maxn],len;

int build(int l,int r)
{
    int root=++tot;//每新建一个节点（根）
    if(l==r) return root;//如果到叶节点了返回根的值，我们要记录下来
    int mid=l+r>>;//二分区间
    ls[root]=build(l,mid);//记录下一层的根，也就是左儿子
    rs[root]=build(mid+,r);//同上
    return root;//返回大根
}
int updata(int l,int r,int root,int k)
{
    int newroot=++tot;//新建的根的编号
    ls[newroot]=ls[root];//记录
    rs[newroot]=rs[root];//建一个等价的节点，左右儿子也是旧根节点的左右儿子
    sum[newroot]=sum[root]+;//每新建一条链增加一个有值的点，所以+1(权值线段树)
    if(l==r) return newroot;
    int mid=l+r>>;
    if(k<=mid) ls[newroot]=updata(l,mid,ls[newroot],k);//
    else rs[newroot]=updata(mid+,r,rs[newroot],k);
    return newroot;
}
int query(int fl,int fr,int l,int r,int k)
{
    int mid=l+r>>,x=sum[ls[fr]]-sum[ls[fl]];//查询区间里的东西，先遍历左儿子，不行再往右跑
    if(l==r) return l;
    else if(k<=x) return query(ls[fl],ls[fr],l,mid,k);//差分了
    else return query(rs[fl],rs[fr],mid+,r,k-x);//差分了
}
int main()
{
    int i,x,l,r,k;
    scanf("%d%d",&n,&m);
    for(i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
        b[i]=a[i];
    }
    sort(b+,b++n);
    len=unique(b+,b++n)-b-;//去重，神仙操作
    //printf("%d\n",len);
    rt[]=build(,len);//根的“tot”（下标，第几个点）
    for(i=;i<=n;i++)//要对每一个节点建树，所以n次加边
    {
        x=lower_bound(b+,b++len,a[i])-b;//离散化，更新相对大小，也就是把所有数的编号弄小
        rt[i]=updata(,len,rt[i-],x);//新根的编号
    }
    for(i=;i<=m;i++)
    {
        scanf("%d%d%d",&l,&r,&k);
        printf("%d\n",b[query(rt[l-],rt[r],,len,k)]);//query返回的是下标，所以要这么长一串。。
    }
    for(int i=;i<=*n;i++)
    {
        //if(sum[i]==0)break;
        printf("%d ",sum[i]);
    }
    return ;
}

（完）