jquery3和layui冲突导，致使用layui.layer.full弹出全屏iframe窗口时高度152px问题
项目中使用的jquery版本是jquery-3.2.1，在使用layui弹出全屏iframe窗口时，iframe窗口顶部总是出现一个152px高的滚动窗口无法实现真正全屏，代码如下：
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<meta name="viewport" content="width=device-width, initial-scale=1, maximum-scale=1">
<title>zqc</title>
<script type="text/javascript" src="js/jquery-3.2.1.min.js"></script>
<link rel="stylesheet" href="layui/css/layui.css">
</head>
<body> <script src="layui/layui.js"></script>
<script>
//一般直接写在一个js文件中
layui.use(['layer', 'form'], function(){
var layer = layui.layer
,form = layui.form; //弹出即全屏
var index = layer.open({
type: 2,
content: 'http://layim.layui.com',
area: ['320px', '195px'],
maxmin: true
});
layer.full(index);
});
</script>
</body>
</html>
就是因为头部引入了 jquery-3.2.1.min.js导致iframe窗口无法全屏，效果如下
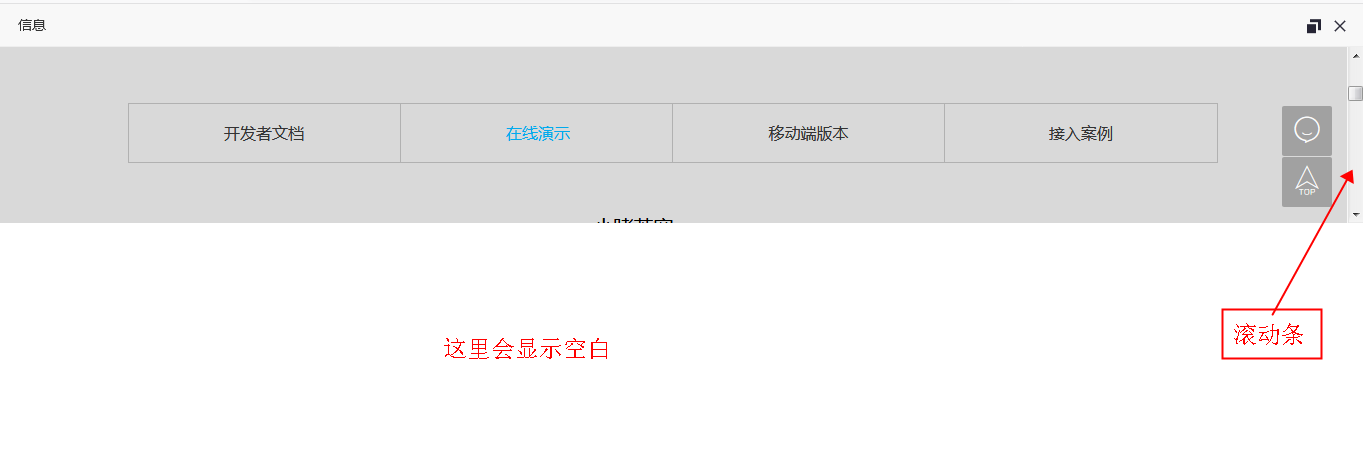
解决办法：
方法一.使用layui内置的jquery
方法二.使用jquery1.X版本，我这里事更换的jquery-1.12.4，解决后代码如下：
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<meta name="viewport" content="width=device-width, initial-scale=1, maximum-scale=1">
<title>zqc</title>
<script type="text/javascript" src="js/jquery-1.12.4.min.js"></script>
<link rel="stylesheet" href="layui/css/layui.css">
</head>
<body> <script src="layui/layui.js"></script>
<script>
//一般直接写在一个js文件中
layui.use(['layer', 'form'], function(){
var layer = layui.layer
,form = layui.form; //弹出即全屏
var index = layer.open({
type: 2,
content: 'http://layim.layui.com',
area: ['320px', '195px'],
maxmin: true
});
layer.full(index);
});
</script>
</body>
</html>
jquery3和layui冲突导，致使用layui.layer.full弹出全屏iframe窗口时高度152px问题的更多相关文章
- JS中通过LayUI的layer.prompt弹出文本输入层，多个按钮回调获取输入值
JS中通过LayUI弹出文本输入层,多个按钮回调: 如图所示,输入文本后点击通过/不通过按钮回调获取输入文本值的实现: 实现JS: layer.prompt({ formType: 2, // 弹出文 ...
- layer重复弹出(layui弹层同时存在多个)的解决方法
layer.open() 同时存在多个;解决 layui 弹层 layer 同时存在多个页面层(iframe)的问题 这个问题其实是疏忽了一些 基础参数(仔细看文档,仔细看文档,仔细看文档) 一.ty ...
- layui之弹出层--从父窗口传递数据到子窗口
原文链接:https://blog.csdn.net/Code_shadow/article/details/80524633 var Index = layer.open({ title: &quo ...
- layui layer.open弹出框获取不了 input框的值
layer.open({ title:'添加管理员', type: 1, content: $('.add_html').html(), btn:['添加', '取消'], btnAlign:'c', ...
- Layui弹出层、日期和时间选择、即时通讯、分页
Layui弹出层.日期和时间选择.即时通讯.分页 弹层组件文档 - layui.layer 对于弹出层的感觉是:layer 至今仍作为 layui 的代表作,她的受众广泛并非偶然,而是这数年来的坚持. ...
- 解决 layui 弹出层（弹框）一闪而过就消失的问题 （转载）
转载: 原文链接:https://blog.csdn.net/qq_20594019/article/details/83956532 本人遇到问题:使用layer.open()弹出页面层,出现弹框闪 ...
- layer/layui弹出层插件bug
<button class="layui-btn" lay-submit lay-filter="formDemo" id="layui-btn ...
- 权限管理系统之LayUI实现页面增删改查和弹出层交互
由于对LayUI框架不太熟悉,昨天抽空看了下LayUI的文档,今天在网上找了使用LayUI进行增删改查相关内容,自己照葫芦画了个瓢,画瓢部分不是很难,主要是下午遇到了一个弹出层的问题耗时比较久. 同一 ...
- Layui弹出层详解
今天空了学习一下弹出层 还是一步步展示把 首先,layer可以独立使用,也可以通过Layui模块化使用.我个人一直是用的模块化的 所以下面素有的都是基于模块化的. 引入好相关文件就可以开始啦 今天放 ...
随机推荐
- Django生成PDF显示在网页上以及解决中文显示乱码的问题
项目地址:https://github.com/PythonerKK/django-generate-pdf/tree/master 这个demo实现了通过用户输入自己的个人信息生成一份简历pdf,来 ...
- Codeforces Round #569 (Div. 2)A. Alex and a Rhombus
A. Alex and a Rhombus 题目链接:http://codeforces.com/contest/1180/problem/A 题目: While playing with geome ...
- CSS清除默认样式代码
html, body, div, ul, li, h1, h2, h3, h4, h5, h6, p, dl, dt, dd, ol, form, input, textarea, th, td, s ...
- 18 | 眼前一亮：带你玩转GUI自动化的测试报告
- 如何将 qsys 子模块设置为参数可调的方式给另外的qsys 调用
Intel FPGA Quartus 软件中的 Qsys工具 也就是 Platform Designer 系统集成工具,可以 图形化界面操作 使用系统自带ip,自定义ip 系统自动生成 ip 间的连接 ...
- Java基础中字符串与字符的注意点！
在Java中,字符的表达与字符串的表达是不一样的!话不多说,直接上代码!!! String a="a"; char a='a'; 其中他们的引号是不一样的
- spring源码深度解析— IOC 之 属性填充
doCreateBean() 主要用于完成 bean 的创建和初始化工作,我们可以将其分为四个过程: createBeanInstance() 实例化 bean populateBean() 属性填充 ...
- C++ 洛谷 P2704 [NOI2001]炮兵阵地
P2704 [NOI2001]炮兵阵地 没学状压DP的看一下 此题意思很简单,如下图,就是十字架上的不能有两个点放炮兵. 在做此题前,先做一下玉米田 玉米田题解 分析: 而m即一行的个数小于等于10, ...
- 【Mysql】索引简介
本文口味:番茄炒蛋,预计阅读:10分钟. 博客又停更了两个月,在这期间,对人生和世界多了许多思考.在人生的不同阶段,会对生活和世界有着不一样的认知,而认知的改变也会直接反应在行为模式之中. 对于生活的 ...
- 把大象装进冰箱：HTTP传输大文件的方法
上次我们谈到了HTTP报文里的div,知道了HTTP可以传输很多种类的数据,不仅是文本,也能传输图片,音频和视频. 早期互联网上传输的基本上都是只有几k大小的文本和小图片,现在的情况则大有不同.网 ...