STL中关于全排列next_permutation以及prev_permutation的用法

这两个函数都包含在algorithm库中。STL提供了两个用来计算排列组合关系的算法，分别是next_permutation和prev_permutation。

一、函数原型

首先我们来看看这两个函数的函数原型：

• next_permutation:

 template< class BidirIt >bool next_permutation( BidirIt first, BidirIt last );
 template< class BidirIt, class Compare >bool next_permutation( BidirIt first, BidirIt last, Compare comp );

• prev_permutation:

 template< class BidirIt >bool prev_permutation( BidirIt first, BidirIt last);
 template< class BidirIt, class Compare >bool prev_permutation( BidirIt first, BidirIt last, Compare comp);

1.参数

first，end ——重新排序的元素范围

comp —— 自定义比较函数

顾名思义，next_permutation就是求下一个排列组合，而prev_permutation就是求上一个排列组合。首先我们必须了解什么是“下一个”排列组合，什么是“前一个”排列组合。考虑由三个字符所组成的序列{a,b,c}。

那么按照字典序排升序他们一共有下面这几种排列方式：

• abc
• acb
• bac
• bca
• cab
• cba

如果给定排列方式P，令P为{acb}，那么next_permutation即求P+1也就是{bac}，prev_permutation也就是求P-1即为{abc}。当然也可以自定义谓词函数进行自定义的“下一个排列组合”。

二、代码演示

下面是示范代码：

 #include <bits/stdc++.h>
 using namespace std;

 int main(){
     int a[] = {,,};
     do{
         for(int i = ; i < ; i++) cout << a[i] << ' ';
         cout << endl;
     }while(next_permutation(a,a+));

     cout << endl;
     do{
         for(int i = ; i < ; i++) cout << a[i] << ' ';
         cout << endl;
     }while(prev_permutation(a,a+));
     return ;
 }

　　预计上面代码的运行结果应该是输出两组1，2，3的排列组合方式，共12行，但实际运行结果如下：

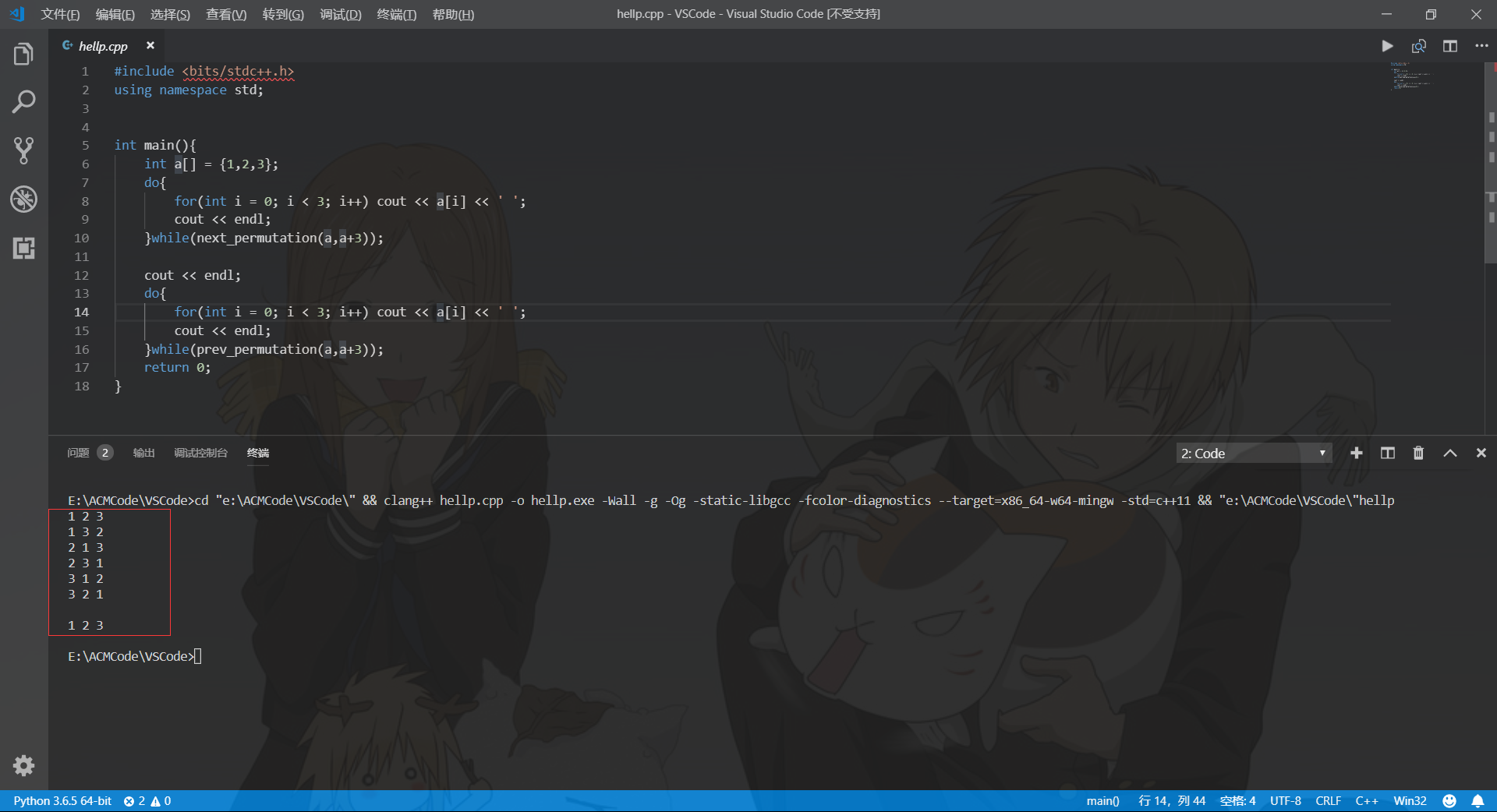
Why？

我们试着输出第一个循环后a数组的排列方式，结果会得到1 2 3，这是因为当next_permutation去找下一个排列组合P+1，找到则排列为下一个排列组合返回true，否则数组变成字典序最小的排列组合（即为重置排列）并返回false，prev_permutation也同理。

三、手动实现

我们先想想如何实现next_permutation，prev_permutation 的原理与之类似。根据字典序，如果排列为正序既从小到大排列，是一组排列组合中最小的排列方式，而逆序既从大到小排列，则是一组排列组合中最大的排列方式。

在n个元素的排列全排列中，从给定排列P 求解下一排列P+1 ，假设两个排列组合有前k位是相同的，那么我们只需要在后面n-k个元素的排列 P(n-k)中求得下一个排列即可。既然我们需要的是后面 n-k位的排列，那么直接从后向前考察。

例如排列 1 2 3 4 5，这是一个正序排列，因此全排列中最小的排列，记为P.

现在要求P+1，设P1=P+1，P1是 1 2 3 5 4. 可以发现P1的前三位和P的前三位完全相同，唯一不同的是后两位顺序颠倒，最后两位从正序的 4 5 变成了逆序的 5 4.

接着求P1+1.设P2 = P1+1，P2是 1 2 4 3 5. 因为最后两位已经是逆序，不可能有字典序更大的排列，因此必须考虑更多的位，在后3个元素中，3 5 4 显然不是逆序，所以存在字典序更大的排列方式，我们由此确定了n-k=3

现在要在 3 5 4 中求得下一个排列，3 5 4 不是一个逆序，是因为 3 后面有元素大于3 。所以我们要在大于3的数字中选择最小的那个和3交换，保证得到最小的首位元素。选择将3和4进行交换，而不是3 和 5，这样得到的首位元素是4. 现在我们得到了排列 4 5 3 。

显然，4 5 3 并不是我们想要的下一个排列，下一个排列是 4 3 5. 观察区别，不难看出，首位元素一定是4，但是5 3 这个子排列是一个逆序排列。将逆序排列反向后，得到的正序排列是所能形成的最小排列，因此，4 3 5 是4 为首位元素所能形成最小排列，而前3 位没有变化，故我们得到了下一排列P2.

另外，大于3的最小元素，即4 ，也是第一个大于3的元素，因为 5 4 是个逆序排列。

对于可重集排列 1 2 3 5 4 3 2 1也同理，首先找到第一个非逆序元素，这里是3，然后从后向前寻找第一个大于3的元素，这里是4，交换，得到 4 5 3 3 2 1 的子排列，然后反向，即可得到下一排列。如果没有找到第一个非逆序元素，那么说明该排列已经是最大排列。

代码：

 template<class T>
 bool next_permutation(T begin, T end){
     T i = end;
     if (begin == end || begin == --i) return false;

     while(){
         T i1 = i,i2;
         if (*--i < *i1) {   //找第k位
             for(i2 = end; *i >= *i2; i2--);//从后往前找到逆序中大于*i的元素的最小元素
             iter_swap(i, i2);
             reverse(i1, end);////将尾部的逆序变成正序
             return true;
         }
         if (i == begin) {
             reverse(begin, end);
             return false;
         }
     }
 }

prev_permutation的代码实现也类似，这里不再给出，各位可以自行尝试。

四、复杂度分析

最多n/2次交换，n为区间长度，平均每次调用使用了3次比较和1.5次交换，时间复杂度为O(n)。