python算法与数据结构-二叉树的代码实现(46)

一、二叉树回忆

　　上一篇我们对数据结构中常用的树做了介绍，本篇博客主要以二叉树为例，讲解一下树的数据结构和代码实现。回顾二叉树：二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）

二、二叉树比链表好在哪里？

看看如下的数据：使用链表形式存放

我们要向查找数据6，需要从头开始查找，找到最后一个，查找比较麻烦。再来看看使用二叉树的形式存储

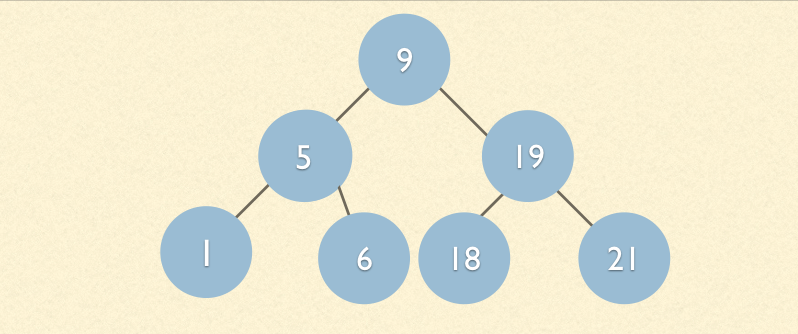
显然，我们很清楚自己要查找的目标大致会在那里出现；

例如查找的目标是6，那么我知道6小于9所以根本不会去看右边的数据；

我们继续看6大于5所以找到啦目标；

换句话说我们只对比了两次找到啦目标；

而对于链表，我们发现6排在了链表的尾部；到此为止我们知道这样的二叉树的确是高效的；

三、二叉树的节点定义（C语言版）

typedef struct N
{
    int data;
    struct N *left_node;
    struct N *right_node;

}Node;

四、定义一个二叉树（C语言版）

typedef struct tree
{
    struct node *root;
}Tree;

我们的树定义得更加简单，注意我们是先定义节点，再定义树；

因为树的定义需要用到节点结构体；

接下来我们需要初始化我们的树

五、初始化树（C语言版）

Tree * init_tree()
{
    Tree *tree = (Tree *)malloc(sizeof(Tree));
    if (tree)
    {
        tree->root = NULL;
    }
    return tree;
}

六、创建节点（C语言版）

Node *make_node(int data)
{
    Node *node = (Node *)malloc(sizeof(Node));
    node->left_node = NULL;
    node->right_node = NULL;
    node->data = data;
    return node;
}

七、插入节点（C语言版）

// 插入节点
Node* insert_node(Tree *tree,int data)
{
    // 判断根节点是否存在
    if (tree->root == NULL)
    {
        // 不存在就创建
        tree->root = make_node(data);
    }
    else
    {
        Node *current = tree->root;
        // 一直循环知道找到准确的插入数据的位置
        while ()
        {
            // 我们的二叉树不允许重复数字插入,相等直接退出
            if (current->data == data)
            {
                return tree->root;
            }
            // 如果要插入的数据比根节点大，就放在右边的子树中
            else if(current->data<data)
            {
                if (current->right_node == NULL)
                {
                    // 创建右节点
                    current->right_node = make_node(data);
                    break;
                }
                current = current->right_node;
            }
            else
            {
                // 如果要插入的数据比根节点小，就放在左边的子树中
                if (current->left_node == NULL)
                {
                    // 创建左节点
                    current->left_node = make_node(data);
                    break;
                }
                current = current->left_node;
            }
        }
    }
    return tree->root;
}

八、树的遍历（C语言版）

void print_inorder(Node *root)
{
    if (root)
    {
        print_inorder(root->left_node);
        printf("data:%d\n",root->data);
        print_inorder(root->right_node);
    }
}

九、树的删除（C语言版）

树的删除比较麻烦，整体分为二种情况：

　　一、要删除的节点左右都有子节点

　　二、要删除的节点只有一个或者0个节点（即有左节点或者右节点或者一个都没有）

其中第一种情况又分几种小情况。例如：我们要删除节点6

　　1.1 我们现在要删除的是节点6，这时候6节点下面的右节点只有一个7，并且7下面没有节点，有一个也一样的，只需要将其右边的节点7替代他的位置即可。

　　

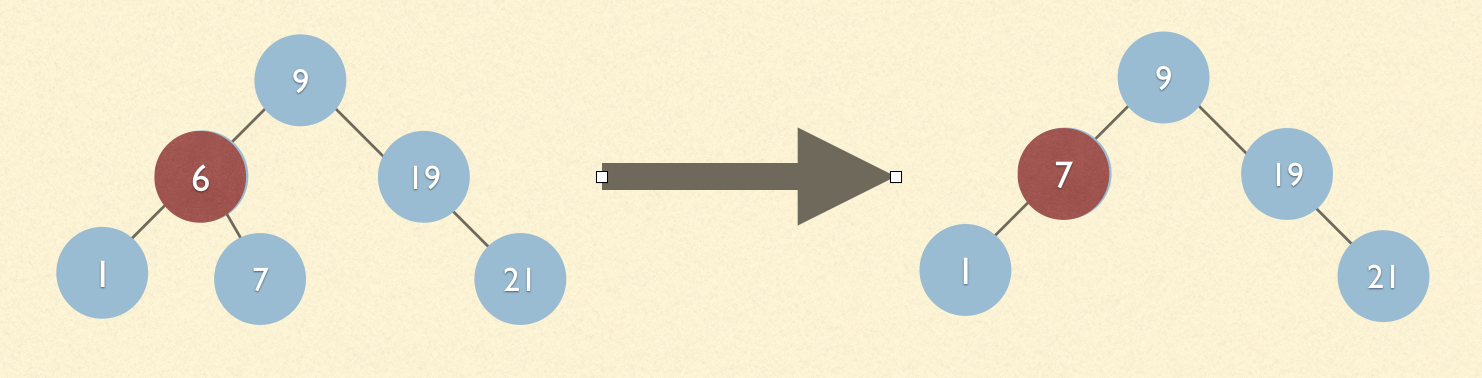
　　1.2 我们现在要删除的是节点6，现在7下面5和8两个节点，如果还是按照上面的思路删除的话，删除之后7下面就有1，5，8三个节点，明显不对

　　

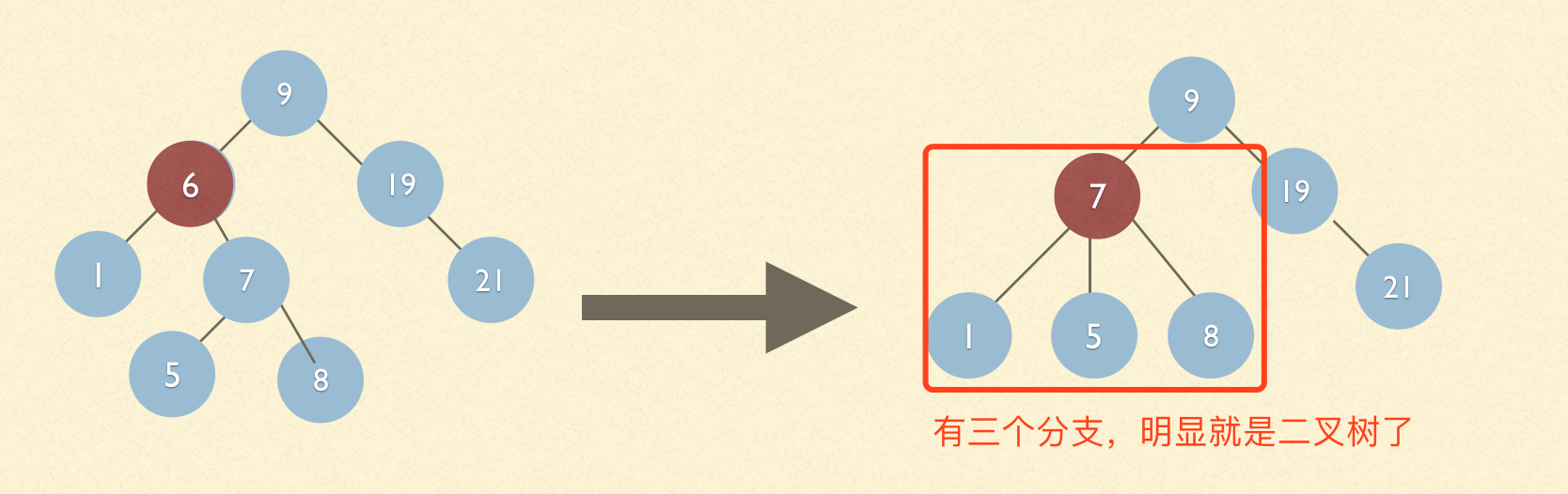
　　正确的做法应该是找到要删除的节点6的右节点7，这时候在找到7的做节点5，去继承删除节点6的位置

　　

　　1.3、以要删除节点6的右节点7为树的左边分支的最小子节点是左节点的情况（很绕口）

　　

　　1.4、以要删除节点6的右节点7为树的左边分支的最小子节点是右节点的情况（很绕口）

　　

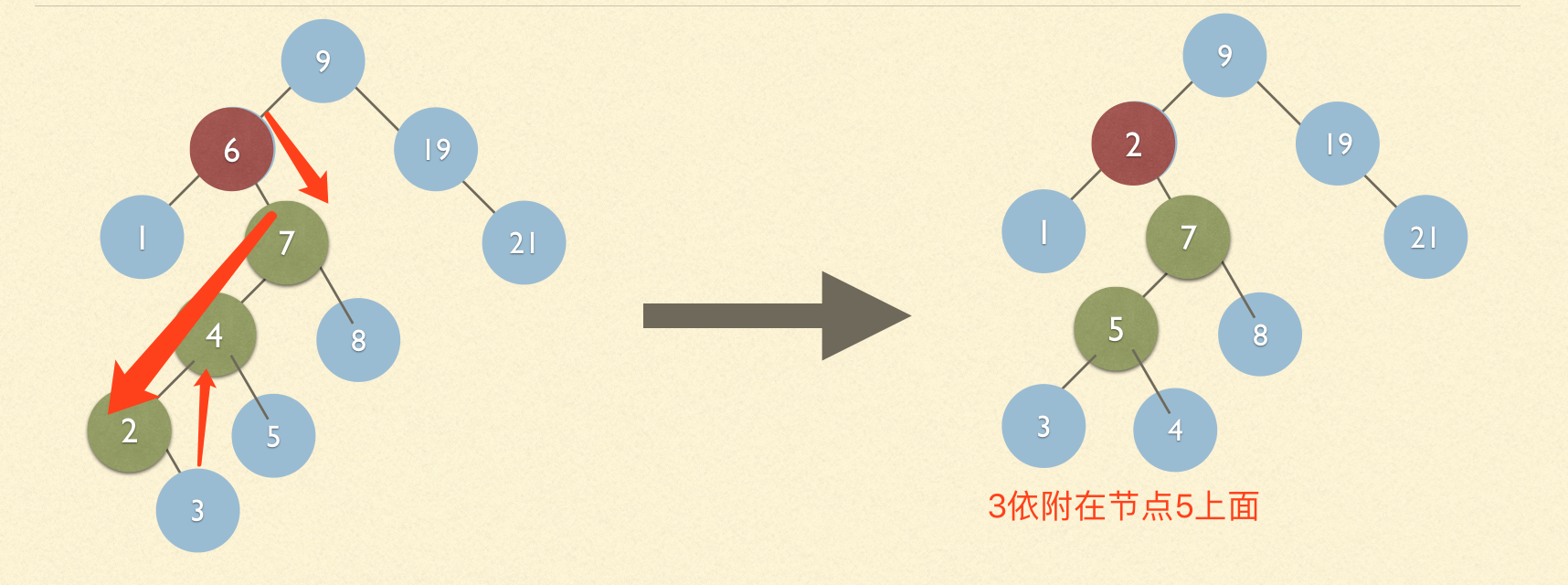
树删除代码的实现

int remove_node(Tree *tree,int data)
{
    if (tree->root != NULL)
    {
        Node *p = NULL;
        Node *s ;
        Node *current = tree->root;

        while ()
        {
            // 根节点都没有直接返回
            if (current == NULL)
            {
                return ;
            }
            // 要删除的节点就是跟节点
            else if(current->data == data)
            {
                break;
            }
            // 要删除的节点在根节点的右边
            else if(current->data<data)
            {
                p = current;
                current = current->right_node;
            }
            // 要删除的节点在根节点的左边
            else
            {
                p=current;
                current = current->left_node;
            }
        }
/**********************上面的代码片段是找到要删除的节点**************************/

        if (current->left_node != NULL && current->right_node != NULL)
        {
            p = current;
            // 找到要删除节点的右节点
            s = current->right_node;
            while (s->left_node != NULL)
            {
                // p = s当current要深入到下一个分叉时，给自己留一个后路；所以保存了自己的前一个备份；
                p = s;
                // 沿着左边一直找到最小的节点
                s = s->left_node;
            }
            current->data = s->data;
            // 最小值在分支的右边
            if ( p->right_node == s)
            {
                p->right_node = s->right_node;
            }
            free(s);
        }
/***************上面的代码片段是根据要删除节点左右都有子节点的情况**************/
        else
        {
            // 左子节点为空，只有右子节点
            if (current->left_node == NULL)
            {
                // 而且要删除的节点是跟节点
                if (p==NULL)
                {
                    // 直接将跟节点的右节点设置为跟节点
                    tree->root = current->right_node;
                }
                else
                {
                    if (p->right_node == current)
                    {
                        p->right_node = current->right_node;
                    }
                    else
                    {
                        p->left_node = current->right_node;
                    }
                }
            }
            // 右子节点为空，只有左子节点
            else
            {
                // 而且要删除的节点是跟节点
                if (p == NULL)
                {
                    tree->root = current->left_node;
                }
                else
                {
                    if (p->right_node == current)
                    {
                        p->right_node = current->left_node;
                    }
                    else
                    {
                        p->left_node = current->left_node;
                    }
                }
            }
        }
/***************上面的代码片段是根据要删除节点左右只有一个或者没有子节点的情况**********/
    }
    return ;
}

十、树的查找（C语言版）

int find_node(Node *root,int data)
{
    if (root == NULL)
    {
        return ;
    }
    else if(root->data == data)
    {
        return ;
    }
    else
    {
        if (root->data <data)
        {
            return find_node(root->right_node, data);
        }
        else
        {
            return find_node(root->left_node, data);
        }
    }
}

十一、树的前序遍历（C语言版）

void preOrder(Node *root)
{
    if (root != NULL)
    {
        printf("%d ",root->data);
        preOrder(root->left_node);
        preOrder(root->right_node);
    }
}

十二、树的中序遍历（C语言版）

void inOrder(Node *root)
{
    if (root != NULL)
    {
        inOrder(root->left_node);
        printf("%d ",root->data);
        inOrder(root->right_node);
    }
}

十三、树的后序遍历(C语言版)

void postOreder(Node *root)
{
    if (root != NULL)
    {
        postOreder(root->left_node);
        postOreder(root->right_node);
        printf("%d ",root->data);
    }

}

十四、树的广度遍历（C语言版）

void level_order(Tree *tree)
{
    Node *node = tree->root;
    Node *queue[];
    int current = ;
    int after_current = ;
    if (node == NULL)
    {
        return;
    }

    queue[current++] = node;
    while (current!=after_current)
    {
        node = queue[after_current++];
        printf("%d ",node->data);
        if (node->left_node != NULL)
        {
            queue[current++] = node->left_node;
        }
        if (node->right_node != NULL)
        {
            queue[current++] = node->right_node;
        }
    }
}

十五、树的python代码实现

由于C语言版写的很详细了，python就简单的实现排序，思路完全一样。

# coding:utf-8

class Node(object):
    """"""
    def __init__(self, item):
        self.elem = item
        self.lchild = None
        self.rchild = None

class Tree(object):
    """二叉树"""
    def __init__(self):
        self.root = None

    def add(self, item):
        node = Node(item)
        if self.root is None:
            self.root = node
            return
        queue = [self.root]
        while queue:
            cur_node = queue.pop(0)
            if cur_node.lchild is None:
                cur_node.lchild = node
                return
            else:
                queue.append(cur_node.lchild)
            if cur_node.rchild is None:
                cur_node.rchild = node
                return
            else:
                queue.append(cur_node.rchild)

    def breadth_travel(self):
        """广度遍历"""
        if self.root is None:
            return
        queue = [self.root]
        while queue:
            cur_node = queue.pop(0)
            print(cur_node.elem, end=" ")
            if cur_node.lchild is not None:
                queue.append(cur_node.lchild)
            if cur_node.rchild is not None:
                queue.append(cur_node.rchild)

    def preorder(self, node):
        """先序遍历"""
        if node is None:
            return
        print(node.elem, end=" ")
        self.preorder(node.lchild)
        self.preorder(node.rchild)

    def inorder(self, node):
        """中序遍历"""
        if node is None:
            return
        self.inorder(node.lchild)
        print(node.elem, end=" ")
        self.inorder(node.rchild)

    def postorder(self, node):
        """后序遍历"""
        if node is None:
            return
        self.postorder(node.lchild)
        self.postorder(node.rchild)
        print(node.elem, end=" ")

if __name__ == "__main__":
    tree = Tree()
    tree.add(5)
    tree.add(2)
    tree.add(3)
    tree.add(7)
    tree.add(4)
    tree.add(8)
    tree.add(6)

    tree.preorder(tree.root)
    print(" ")
    tree.inorder(tree.root)
    print(" ")
    tree.postorder(tree.root)
    print(" ")
    tree.breadth_travel()

运行结果为：

5 2 7 4 3 8 6
7 2 4 5 8 3 6
7 4 2 8 6 3 5
5 2 3 7 4 8 6 

写到此处以吐血，你看到次数也吐血了吧。