2019牛客暑期多校训练营（第九场） E-All men are brothers（并查集+组合数学）

>传送门<

题意：最初有 n个人且互不认识，接下来 m行，每行有 x，y表示x和y交朋友，朋友关系满足自反性和传递性，每次输出当前选取4个人且互不认识的方案数。

思路：比赛的时候知道是用并查集做，然而也只是知道，具体的思维还没有想到这一块，还是太菜了，得去多做多想~

并查集合并操作可以理解为使得两个集合的人互相成为朋友，也就是两个集合并在了一起，答案是要求从所有人中挑出四个互相不是朋友的四个人，比较基础的组合数学知识，但因为每个集合的大小预先不知，所以变得难以计算。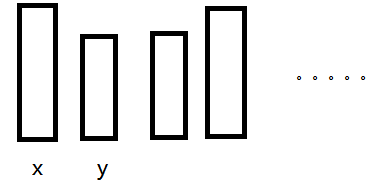

假设我们现在算出了合并前的答案，在合并x和y时，设 num[x]为x所在集合的集合大小，num[y] 同理。考虑这两个集合对答案的贡献，有三种情况：

1. 从x所在集合中取一个人，然后再从其他非y集合中挑选出三个互不在同一集合的人
2. 从y所在集合中取一个人，然后再从其他非x集合中挑选出三个互不在同一集合的人
3. 从x，y所在集合中各取一个人，然后再从其他集合中挑选出两个互不在同一集合的人

考虑合并之后

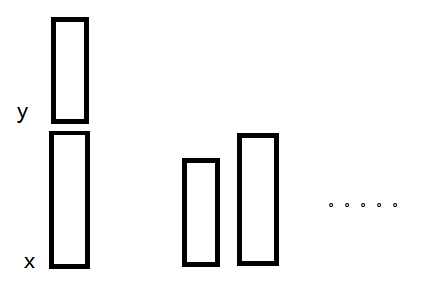
可以发现合并之后x和y在同一集合，仔细观察上面说到的情况1、2，它们对答案的贡献并没有因为合并操作而改变。只有情况3，在合并之后，该贡献被消灭，所以要用上一次的答案减去这个情况，就是合并之后的答案。

那么该怎么计算呢？情况3的答案等同于（从x，y所在集合中各取一个人的情况总数）*（从其他集合中挑选出两个互不在同一集合的人的情况总数）

从这两个集合中各选一个人的情况是很好求的：num[x]*num[y]。

好，现在就只剩下求从其他集合中挑选出两个互不在同一集合的人的情况总数，这一看就有点不好求，不要紧，我们开动脑瓜子想一想。

现在我们有两种做法，一种是直接求，一种是间接的求。

我们先来看直接求的那一种

我们假设K是从所有集合中挑选出两个互不在同一集合的人的情况总数，那么我们用K减去从所有集合中挑选出两个互不在同一集合的人(其中至少有一个来自x或y)，那么相减的结果不就是从其他集合中挑选出两个互不在同一集合的人的情况总数么，对不对，仔细想想肯定是这样的

那答案就出来了，如果x，y不需要合并的话(即在同一集合内)，答案自然也就不需要更新，直接输出上一次的答案即可，其余部分按并查集处理就OK了

 Code

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1e5+;

int n, m, x, y;
int f[maxn];
ll num[maxn];
ll K; //K表示从所有集合中挑选2个互不在同一集合的人的方案数
unsigned long long C; //C表示从所有集合中挑选4个互不在同一集合的人的方案数
int get(int x){
    if (f[x]==x) return x;
    return f[x]=get(f[x]);
}
void unite(int a,int b){
    ll p = num[a]*num[b]; //从a, b所在集合中各取1个人的情况
    ll q = num[a]*(n-num[a])+num[b]*(n-num[b])-num[a]*num[b]; //从所有集合挑选2个人(至少有一个来自a或b)的情况
    ll k = K-q; //再从其他集合中挑选2个互不在同一集合的人
    C -= p*k;
    K = K-num[a]*num[b]; //由于a, b集合合并，K减去在同一集合中选2个人的方案
    f[a] = b;
    num[b] += num[a];
}
void init(){
    C=1ull*n*(n-)/*(n-)/*(n-)/; //C初始化为从所有数中选4个的方案总数
    K = 1ll*n*(n-)/; //K初始化从所有数中选2个的方案总数
    for (int i = ; i <= n; i++) f[i] = i, num[i] = ;
}
int main()
{
    scanf("%d%d", &n, &m);
    init();
    printf("%llu\n",C);
    while(m--){
        scanf("%d%d",&x,&y);
        if (get(x)!=get(y))
            unite(f[x],f[y]);
        printf("%llu\n",C);
    }
}

---

参考文章：
https://www.cnblogs.com/1625--H/p/11359772.html