每日一题 - 剑指 Offer 48. 最长不含重复字符的子字符串

题目信息

• 时间： 2019-07-02

• 题目链接：Leetcode

• tag： 动态规划 哈希表

• 难易程度：中等

• 题目描述：

  请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。

示例1:

输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例2:

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例3:

输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

注意

1. s.length <= 40000

解题思路

本题难点

长度为 N 的字符串共有 (1+N)N/2 个子字符串（复杂度为 O(N^2 ) ），判断长度为 N 的字符串是否有重复字符的复杂度为 O(N) ，使用暴力法解决的复杂度为 O(N^3) 。

具体思路

考虑使用动态规划降低时间复杂度。

• 状态定义：设动态规划列表 dp ，dp[j] 代表以字符 s[j 为结尾的 “最长不重复子字符串” 的长度。
• 转移方程：固定右边界 j ，设字符 s[j] 左边距离最近的相同字符为 s[i] ，即 s[i]=s[j] 。
  • 当 i<0时，即 s[j] 左边无相同字符，则 dp[j]=dp[j−1]+1 ；
  • 当 dp[j−1] < j−i 时，说明字符 s[i] 在子字符串 dp[j−1] 区间之外 ，则 dp[j]=dp[j−1]+1 ；
  • 当 dp[j−1] > j−i 时，说明字符 s[i] 在子字符串 dp[j−1] 区间之中 ，则 dp[j] 的左边界由 s[i] 决定，即 dp[j]=j−i ；

注意:当 i<0 时，由于 dp[j−1]≤j 恒成立，因而 dp[j−1]<j−i 恒成立，因此分支 1. 和 2. 可被合并。

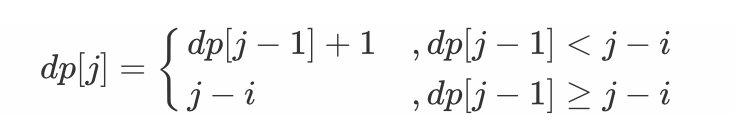
代码

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> dic = new HashMap<>();
        int res = 0, tmp = 0;
        for(int j = 0; j < s.length(); j++) {
            int i = dic.getOrDefault(s.charAt(j), -1); // 获取索引 i
            dic.put(s.charAt(j), j); // 更新哈希表
            tmp = tmp < j - i ? tmp + 1 : j - i; // dp[j - 1] -> dp[j]
            res = Math.max(res, tmp); // max(dp[j - 1], dp[j])
        }
        return res;
    }
}

复杂度分析：

• 时间复杂度 O(N) ：其中 N为字符串长度，动态规划需遍历计算 dp列表。
• 空间复杂度 O(1) ： 字符的 ASCII 码范围为 0 ~ 127 ，哈希表 dic 最多使用 O(128)=O(1) 大小的额外空间。

其他优秀解答

解题思路

双指针 + 哈希表

哈希表 dic统计： 指针 j遍历字符 s，哈希表统计字符 s[j]最后一次出现的索引 。

更新左指针 i ： 根据上轮左指针 i 和 dic[s[j]] ，每轮更新左边界 i ，保证区间 [i+1,j] 内无重复字符且最大

更新结果 res ： 取上轮 res 和本轮双指针区间 [i+1,j] 的宽度（即 j−i ）中的最大值。

代码

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character,Integer> dic = new HashMap<>();
        int i = -1,res = 0;
      //遍历字符串 s
        for(int j = 0; j < s.length();j++){
          //遍历到 s[j] 时，可通过访问哈希表 dic[s[j]] 获取最近的相同字符的索引 i
            if(dic.containsKey(s.charAt(j))){
              //取最大值因为防止abba的情况出现
                i  = Math.max(i,dic.get(s.charAt(j)));
            }
          //使用哈希表统计 各字符最后一次出现的索引位置
            dic.put(s.charAt(j),j);
            res = Math.max(res,j-i);
        }
        return res;
    }
}