[区间+线性dp]数字游戏

题目描述

丁丁最近沉迷于一个数字游戏之中。这个游戏看似简单，但丁丁在研究了许多天之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。游戏是这样的，在你面前有一圈整数（一共\(n\)个），你要按顺序将其分为\(m\)个部分，各部分内的数字相加，相加所得的\(m\)个结果对\(10\)取模后再相乘，最终得到一个数\(k\)。游戏的要求是使你所得的\(k\)最大或者最小。

例如，对于下面这圈数字（\(n=4,m=2\)）：

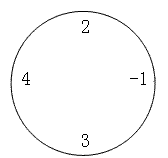
要求最小值时，\(((2−1) mod 10)×((4+3) mod 10)=1×7=7\)，要求最大值时，为\(((2+4+3) mod 10)×(−1 mod 10)=9×9=81\)。特别值得注意的是，无论是负数还是正数，对\(10\)取模的结果均为非负值。

丁丁请你编写程序帮他赢得这个游戏。

输入格式

输入文件第一行有两个整数，\(n(1≤n≤50)\)和\(m(1≤m≤9)\)。以下\(n\)行每行有个整数，其绝对值\(≤10^4\)，按顺序给出圈中的数字，首尾相接。

输出格式

输出文件有\(2\)行，各包含\(1\)个非负整数。第\(1\)行是你程序得到的最小值，第\(2\)行是最大值。

输入 #1

4 2

4

3

-1

2

输出 #1

7

81

分析

对于这种数据，我这种蒟蒻都能看出来，相信很多dalao看到都能一眼就看出来要把环换成链，这是第一个思想。

然后第二个思想就是取模的问题，由于负数取模应为正，假设这个数为\(n\)，我们就可以写一个函数来进行取模运算，也就是\((n\%10+10)\%10\),为什么要这么处理呢，这样就可以把负数取完模变为正，而对于正数就毫无影响，这是一个比较巧妙也重要的处理。

第三个就是前缀和，因为要求和，所以利用前缀和就可以很大的提高效率，思想也会比较明了。

根据dp思想，我们就可以进行状态转移。开一个\(dp\)数组，\(dp[i][j][len]\)代表从\(i\)到\(j\)分成\(len\)段的大小，依次枚举段数，左右端点，和断点，每一次从\(i\)到\(j\)都是由上一个从\(i\)到断点\(c\)分成\(len-1\)段的状态转移而来，转移的过程就是乘上从\(j\)到\(c\)的前缀和取模。我们令取模的函数为\(Mod\)，那么状态转移方程如下：（最大值和最小值一样，唯一要注意的是，最大值初始为\(0\)，最小值每一次转移要改为\(0x3f3f3f3f\)）

\[f1[l][r][len] = min(f1[l][r][len],f1[l][k][len-1]*Mod(sum[r]-sum[k]));\\
f2[l][r][len] = max(f2[l][r][len],f2[l][k][len-1]*Mod(sum[r]-sum[k]));\]

最终再从头到尾扫一遍得结果。

代码

#include<bits/stdc++.h>
using namespace std;
int Mod(int x){//取模优化
	return (x%10+10)%10;
}
int n,m;
const int maxn = 105;
int sum[maxn],a[maxn];
int f1[maxn][maxn][10],f2[maxn][maxn][10];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;++i){
		cin>>a[i];
		a[i+n] = a[i];//环变链
	}
	for(int i=1;i<=2*n;++i){//求前缀和
		sum[i] = sum[i-1]+a[i];
	}
	for(int i=1;i<=2*n;++i){//初始化，分1段时的值
		for(int j=1;j<=2*n;++j){
			f1[i][j][1] = f2[i][j][1] = Mod(sum[j] - sum[i-1]);
		}
	}
	for(int len=2;len<=m;++len){//枚举分成多少段
		for(int l=1;l<=n;++l){//枚举左端点
			for(int r=l+len-1;r<=l+n-1;++r){//枚举右端点
				f1[l][r][len]=0x3f3f3f3f;//求最小值初始化
				for(int k=l+len-2;k<r;++k){//枚举断点
					f1[l][r][len] = min(f1[l][r][len],f1[l][k][len-1]*Mod(sum[r]-sum[k]));
					f2[l][r][len] = max(f2[l][r][len],f2[l][k][len-1]*Mod(sum[r]-sum[k]));

				}
			}
		}
	}
	int Max = f2[1][n][m];
	int Min = f1[1][n][m];
	for(int i=1;i<=n;++i){//从头到尾扫一边
		Max = max(Max,f2[i][i+n-1][m]);
		Min = min(Min,f1[i][i+n-1][m]);
	}
	cout<<Min<<endl<<Max<<endl;
        //Vocanda

}